ML | Introducción a las circunvoluciones estriadas

Comencemos este artículo con una pregunta básica: «¿Por qué se requieren relleno y circunvoluciones con zancadas?»

Supongamos que tenemos una imagen con dimensiones de nxn . Si está enrevesado con un filtro fxf , entonces las dimensiones de la imagen obtenida son .

Ejemplo:
Considere una imagen de 6 x 6 como se muestra en la figura a continuación. Debe enrollarse con un filtro de 3 x 3 . La convolución se realiza mediante la multiplicación por elementos.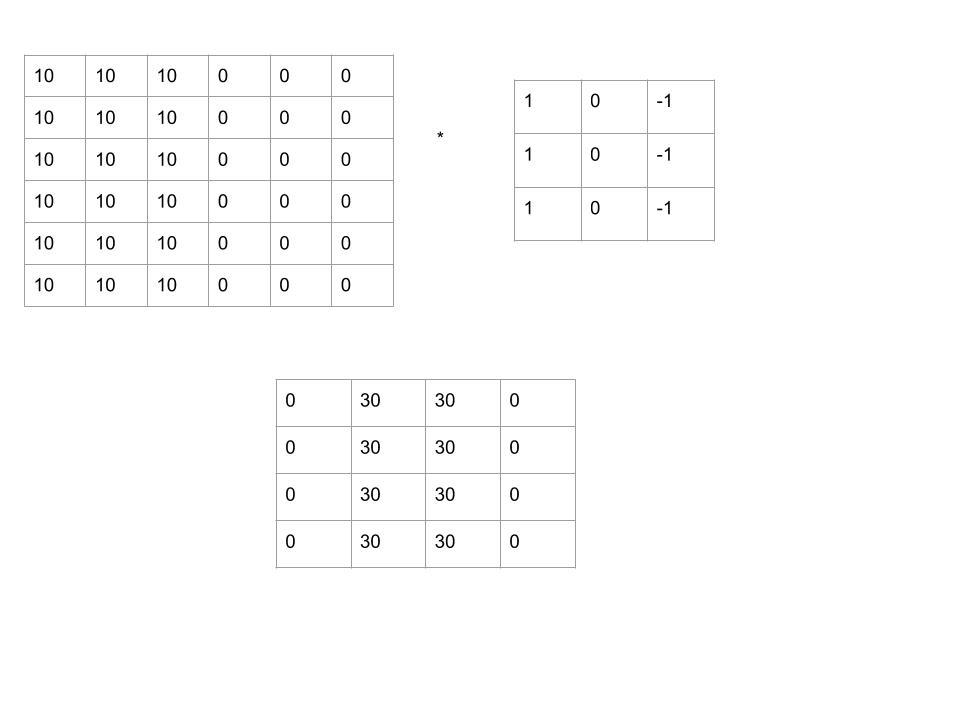

Figura 1: Imagen obtenida después de la convolución de una imagen de 6×6 con un filtro de 3×3 y s=0


Figura 2: Filtro de 6 x 6

Figura 3: filtro 3 x 3

Figura 4: Multiplicación inteligente de elementos
Pero hay dos desventajas de esta convolución:

1. Al aplicar el filtro convolucional cada vez, la imagen original se hunde. es decir, la imagen de salida tiene dimensiones más pequeñas que la imagen de entrada original, lo que puede provocar la pérdida de información.
2. Los píxeles en la esquina de la imagen se usan solo en una de las salidas que los píxeles en el medio, lo que conduce a una gran pérdida de información.

Para evitarlo, se requiere relleno. Además, a veces sucede que tenemos una imagen de entrada muy grande que debe ser complicada con un filtro fxf que puede ser computacionalmente muy costoso. En esta situación, se utilizan zancadas. Es por eso que el relleno y los pasos son uno de los bloques de construcción más básicos de las redes neuronales convolucionales.

Dimensiones de la imagen de salida:

Tengamos una imagen nxn para ser complicada con un filtro fxf . Suponga un borde de relleno de p píxeles y un paso s , entonces las dimensiones de la imagen de salida obtenida son

La cantidad de zancada debe seleccionarse de modo que se requieran cálculos comparativamente menores y la pérdida de información debe ser mínima.
Figura 5: Imagen obtenida tras la convolución de una imagen de 6×6 con un filtro de 3×3 y una zancada de 2