Escriba un programa eficiente para contar el número de 1 en la representación binaria de un número entero.
Ejemplos:
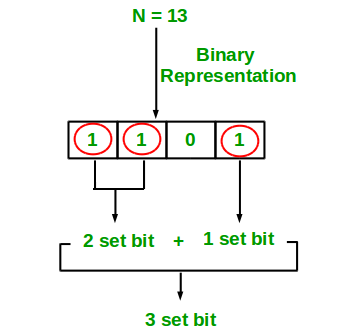
Input : n = 6 Output : 2 Binary representation of 6 is 110 and has 2 set bits Input : n = 13 Output : 3 Binary representation of 13 is 1101 and has 3 set bits
1. Método simple Recorra todos los bits en un entero, verifique si un bit está configurado y si lo está, luego incremente el conteo de bits configurado. Vea el programa a continuación.
C++
// C++ program to Count set
// bits in an integer
#include <bits/stdc++.h>
using namespace std;
/* Function to get no of set bits in binary
representation of positive integer n */
unsigned int countSetBits(unsigned int n)
{
unsigned int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
/* Program to test function countSetBits */
int main()
{
int i = 9;
cout << countSetBits(i);
return 0;
}
// This code is contributed
// by Akanksha Rai
C
// C program to Count set
// bits in an integer
#include <stdio.h>
/* Function to get no of set bits in binary
representation of positive integer n */
unsigned int countSetBits(unsigned int n)
{
unsigned int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
/* Program to test function countSetBits */
int main()
{
int i = 9;
printf("%d", countSetBits(i));
return 0;
}
Java
// Java program to Count set
// bits in an integer
import java.io.*;
class countSetBits {
/* Function to get no of set
bits in binary representation
of positive integer n */
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
// driver program
public static void main(String args[])
{
int i = 9;
System.out.println(countSetBits(i));
}
}
// This code is contributed by Anshika Goyal.
Python3
# Python3 program to Count set # bits in an integer # Function to get no of set bits in binary # representation of positive integer n */ def countSetBits(n): count = 0 while (n): count += n & 1 n >>= 1 return count # Program to test function countSetBits */ i = 9 print(countSetBits(i)) # This code is contributed by # Smitha Dinesh Semwal
C#
// C# program to Count set
// bits in an integer
using System;
class GFG {
// Function to get no of set
// bits in binary representation
// of positive integer n
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
// Driver Code
public static void Main()
{
int i = 9;
Console.Write(countSetBits(i));
}
}
// This code is contributed by Sam007
PHP
<?php
// PHP program to Count set
// bits in an integer
// Function to get no of set
// bits in binary representation
// of positive integer n
function countSetBits($n)
{
$count = 0;
while ($n)
{
$count += $n & 1;
$n >>= 1;
}
return $count;
}
// Driver Code
$i = 9;
echo countSetBits($i);
// This code is contributed by ajit
?>
Javascript
<script>
// Javascript program to Count set
// bits in an integer
/* Function to get no of set bits in binary
representation of positive integer n */
function countSetBits(n)
{
var count = 0;
while (n)
{
count += n & 1;
n >>= 1;
}
return count;
}
/* Program to test function countSetBits */
var i = 9;
document.write(countSetBits(i));
// This code is contributed by noob2000.
</script>
Producción :
2
Complejidad de tiempo: O (logn)
Espacio Auxiliar: O(1)
Enfoque recursivo:
C++
// cpp implementation of recursive approach to find the
// number of set bits in binary representation of positive
// integer n
#include <bits/stdc++.h>
using namespace std;
// recursive function to count set bits
int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
// if last bit set add 1 else add 0
return (n & 1) + countSetBits(n >> 1);
}
// driver code
int main()
{
int n = 9;
// function calling
cout << countSetBits(n);
return 0;
}
// This code is contributed by Sania Kumari Gupta (kriSania804)
C
// cpp implementation of recursive approach to find the
// number of set bits in binary representation of positive
// integer n
#include <stdio.h>
// recursive function to count set bits
int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
// if last bit set add 1 else add 0
return (n & 1) + countSetBits(n >> 1);
}
// driver code
int main()
{
int n = 9;
// function calling
printf("%d", countSetBits(n));
return 0;
}
// This code is contributed by Sania Kumari Gupta (kriSania804)
Java
// Java implementation of recursive
// approach to find the number
// of set bits in binary representation
// of positive integer n
import java.io.*;
class GFG {
// recursive function to count set bits
public static int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
// if last bit set add 1 else add 0
return (n & 1) + countSetBits(n >> 1);
}
// Driver code
public static void main(String[] args)
{
// get value from user
int n = 9;
// function calling
System.out.println(countSetBits(n));
}
}
// This code is contributes by sunnysingh
Python3
# Python3 implementation of recursive # approach to find the number of set # bits in binary representation of # positive integer n def countSetBits( n): # base case if (n == 0): return 0 else: # if last bit set add 1 else # add 0 return (n & 1) + countSetBits(n >> 1) # Get value from user n = 9 # Function calling print( countSetBits(n)) # This code is contributed by sunnysingh
C#
// C# implementation of recursive
// approach to find the number of
// set bits in binary representation
// of positive integer n
using System;
class GFG {
// recursive function
// to count set bits
public static int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
// if last bit set
// add 1 else add 0
return (n & 1) + countSetBits(n >> 1);
}
// Driver code
static public void Main()
{
// get value
// from user
int n = 9;
// function calling
Console.WriteLine(countSetBits(n));
}
}
// This code is contributed by aj_36
PHP
<?php
// PHP implementation of recursive
// approach to find the number of
// set bits in binary representation
// of positive integer n
// recursive function
// to count set bits
function countSetBits($n)
{
// base case
if ($n == 0)
return 0;
else
// if last bit set
// add 1 else add 0
return ($n & 1) +
countSetBits($n >> 1);
}
// Driver code
// get value from user
$n = 9;
// function calling
echo countSetBits($n);
// This code is contributed by m_kit.
?>
Javascript
<script>
// Javascript implementation of recursive
// approach to find the number
// of set bits in binary representation
// of positive integer n
// recursive function to count set bits
function countSetBits(n)
{
// base case
if (n == 0)
return 0;
else
// if last bit set add 1 else add 0
return (n & 1) + countSetBits(n >> 1);
}
// driver code
// get value from user
let n = 9;
// function calling
document.write(countSetBits(n));
// This code is contributed by Mayank Tyagi
</script>
Producción :
2
Complejidad de tiempo: O (log n)
Espacio Auxiliar: O(1)
2. Algoritmo de Brian Kernighan:
Restar 1 de un número decimal voltea todos los bits después del bit establecido más a la derecha (que es 1), incluido el bit establecido más a la derecha.
por ejemplo:
10 en binario es 00001010
9 en binario es 00001001
8 en binario es 00001000
7 en binario es 00000111
Así que si restamos un número por 1 y lo hacemos bit a bit y consigo mismo (n & (n-1)), desarmamos el bit establecido más a la derecha. Si hacemos n & (n-1) en un bucle y contamos el número de veces que se ejecuta el bucle, obtenemos el número de bits establecido.
La belleza de esta solución es que la cantidad de veces que se repite es igual a la cantidad de bits establecidos en un entero dado.
1 Initialize count: = 0
2 If integer n is not zero
(a) Do bitwise & with (n-1) and assign the value back to n
n: = n&(n-1)
(b) Increment count by 1
(c) go to step 2
3 Else return count
Implementación del Algoritmo de Brian Kernighan:
C++
// C++ program to Count set
// bits in an integer
#include <iostream>
using namespace std;
class gfg {
/* Function to get no of set bits in binary
representation of passed binary no. */
public:
unsigned int countSetBits(int n)
{
unsigned int count = 0;
while (n) {
n &= (n - 1);
count++;
}
return count;
}
};
/* Program to test function countSetBits */
int main()
{
gfg g;
int i = 9;
cout << g.countSetBits(i);
return 0;
}
C
// C program to Count set
// bits in an integer
#include <stdio.h>
/* Function to get no of set bits in binary
representation of passed binary no. */
unsigned int countSetBits(int n)
{
unsigned int count = 0;
while (n) {
n &= (n - 1);
count++;
}
return count;
}
/* Program to test function countSetBits */
int main()
{
int i = 9;
printf("%d", countSetBits(i));
getchar();
return 0;
}
Java
// Java program to Count set
// bits in an integer
import java.io.*;
class countSetBits {
/* Function to get no of set
bits in binary representation
of passed binary no. */
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
n &= (n - 1);
count++;
}
return count;
}
// driver program
public static void main(String args[])
{
int i = 9;
System.out.println(countSetBits(i));
}
}
// This code is contributed by Anshika Goyal.
Python3
# Function to get no of set bits in binary # representation of passed binary no. */ def countSetBits(n): count = 0 while (n): n &= (n-1) count+= 1 return count # Program to test function countSetBits i = 9 print(countSetBits(i)) # This code is contributed by # Smitha Dinesh Semwal
C#
// C# program to Count set
// bits in an integer
using System;
class GFG {
/* Function to get no of set
bits in binary representation
of passed binary no. */
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
n &= (n - 1);
count++;
}
return count;
}
// Driver Code
static public void Main()
{
int i = 9;
Console.WriteLine(countSetBits(i));
}
}
// This code is contributed by ajit
PHP
<?php
/* Function to get no of
set bits in binary
representation of passed
binary no. */
function countSetBits($n)
{
$count = 0;
while ($n)
{
$n &= ($n - 1) ;
$count++;
}
return $count;
}
// Driver Code
$i = 9;
echo countSetBits($i);
// This code is contributed
// by akt_mit
?>
Javascript
<script>
// JavaScript program to Count set
// bits in an integerclass
/* Function to get no of set
bits in binary representation
of passed binary no. */
function countSetBits(n)
{
var count = 0;
while (n > 0)
{
n &= (n - 1);
count++;
}
return count;
}
// driver program
var i = 9;
document.write(countSetBits(i));
// This code is contributed by 29AjayKumar
</script>
Producción :
2
Ejemplo para el algoritmo de Brian Kernighan:
n = 9 (1001) count = 0 Since 9 > 0, subtract by 1 and do bitwise & with (9-1) n = 9&8 (1001 & 1000) n = 8 count = 1 Since 8 > 0, subtract by 1 and do bitwise & with (8-1) n = 8&7 (1000 & 0111) n = 0 count = 2 Since n = 0, return count which is 2 now.
Complejidad de tiempo: O (logn)
Espacio Auxiliar: O(1)
Enfoque recursivo:
C++
// CPP implementation for recursive
// approach to find the number of set
// bits using Brian Kernighan’s Algorithm
#include <bits/stdc++.h>
using namespace std;
// recursive function to count set bits
int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
// driver code
int main()
{
// get value from user
int n = 9;
// function calling
cout << countSetBits(n);
return 0;
}
// This code is contributed by Raj.
Java
// Java implementation for recursive
// approach to find the number of set
// bits using Brian Kernighan Algorithm
import java.io.*;
class GFG {
// recursive function to count set bits
public static int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
// Driver function
public static void main(String[] args)
{
// get value from user
int n = 9;
// function calling
System.out.println(countSetBits(n));
}
}
// This code is contributed by sunnysingh
Python3
# Python3 implementation for # recursive approach to find # the number of set bits using # Brian Kernighan’s Algorithm # recursive function to count # set bits def countSetBits(n): # base case if (n == 0): return 0 else: return 1 + countSetBits(n & (n - 1)) # Get value from user n = 9 # function calling print(countSetBits(n)) # This code is contributed by sunnysingh
C#
// C# implementation for recursive
// approach to find the number of set
// bits using Brian Kernighan Algorithm
using System;
class GFG {
// recursive function
// to count set bits
public static int countSetBits(int n)
{
// base case
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
// Driver Code
static public void Main()
{
// get value from user
int n = 9;
// function calling
Console.WriteLine(countSetBits(n));
}
}
// This code is contributed by aj_36
PHP
<?php
// PHP implementation for
// recursive approach to
// find the number of set
// bits using Brian
// Kernighan’s Algorithm
// recursive function to
// count set bits
function countSetBits($n)
{
// base case
if ($n == 0)
return 0;
else
return 1 +
countSetBits($n &
($n - 1));
}
// Driver Code
// get value from user
$n = 9;
// function calling
echo countSetBits($n);
// This code is contributed by ajit.
?>
Javascript
<script>
// Javascript implementation for recursive
// approach to find the number of set
// bits using Brian Kernighan’s Algorithm
// recursive function to count set bits
function countSetBits(n)
{
// base case
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
// driver code
// get value from user
var n = 9;
// function calling
document.write(countSetBits(n));
</script>
Producción :
2
Complejidad de tiempo: O (logn)
Espacio Auxiliar: O(1)
3. Uso de la tabla de búsqueda: Podemos contar bits en tiempo O(1) usando la tabla de búsqueda.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
int BitsSetTable256[256];
// Function to initialise the lookup table
void initialize()
{
// To initially generate the
// table algorithmically
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++)
{
BitsSetTable256[i] = (i & 1) +
BitsSetTable256[i / 2];
}
}
// Function to return the count
// of set bits in n
int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff] +
BitsSetTable256[(n >> 8) & 0xff] +
BitsSetTable256[(n >> 16) & 0xff] +
BitsSetTable256[n >> 24]);
}
// Driver code
int main()
{
// Initialise the lookup table
initialize();
int n = 9;
cout << countSetBits(n);
}
// This code is contributed by Sanjit_Kumar
Java
// Java implementation of the approach
class GFG {
// Lookup table
static int[] BitsSetTable256 = new int[256];
// Function to initialise the lookup table
public static void initialize()
{
// To initially generate the
// table algorithmically
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++) {
BitsSetTable256[i] = (i & 1) + BitsSetTable256[i / 2];
}
}
// Function to return the count
// of set bits in n
public static int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
// Driver code
public static void main(String[] args)
{
// Initialise the lookup table
initialize();
int n = 9;
System.out.print(countSetBits(n));
}
}
Python
# Python implementation of the approach BitsSetTable256 = [0] * 256 # Function to initialise the lookup table def initialize(): # To initially generate the # table algorithmically BitsSetTable256[0] = 0 for i in range(256): BitsSetTable256[i] = (i & 1) + BitsSetTable256[i // 2] # Function to return the count # of set bits in n def countSetBits(n): return (BitsSetTable256[n & 0xff] + BitsSetTable256[(n >> 8) & 0xff] + BitsSetTable256[(n >> 16) & 0xff] + BitsSetTable256[n >> 24]) # Driver code # Initialise the lookup table initialize() n = 9 print(countSetBits(n)) # This code is contributed by SHUBHAMSINGH10
C#
// C# implementation of the approach
using System;
using System.Collections.Generic;
class GFG
{
// Lookup table
static int[] BitsSetTable256 = new int[256];
// Function to initialise the lookup table
public static void initialize()
{
// To initially generate the
// table algorithmically
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++)
{
BitsSetTable256[i] = (i & 1) + BitsSetTable256[i / 2];
}
}
// Function to return the count
// of set bits in n
public static int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
// Driver code
public static void Main(String[] args)
{
// Initialise the lookup table
initialize();
int n = 9;
Console.Write(countSetBits(n));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// javascript implementation of the approach
var BitsSetTable256 = Array.from({length: 256}, (_, i) => 0);
// Function to initialise the lookup table
function initialize()
{
// To initially generate the
// table algorithmically
BitsSetTable256[0] = 0;
for (var i = 0; i < 256; i++) {
BitsSetTable256[i] = (i & 1) +
BitsSetTable256[parseInt(i / 2)];
}
}
// Function to return the count
// of set bits in n
function countSetBits(n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
// Driver code
// Initialise the lookup table
initialize();
var n = 9;
document.write(countSetBits(n));
// This code is contributed by 29AjayKumar
</script>
2
Complejidad de tiempo: O(1)
Como se realizan operaciones de tiempo constante
Espacio Auxiliar: O(1)
Como se utiliza espacio adicional constante
Podemos encontrar un uso para contar bits establecidos en Contar el número de bits que se cambiarán para convertir A en B.
Nota: En GCC, podemos contar directamente los bits establecidos usando __builtin_popcount(). Entonces podemos evitar una función separada para contar bits establecidos.
C++
// C++ program to demonstrate __builtin_popcount()
#include <iostream>
using namespace std;
int main()
{
cout << __builtin_popcount(4) << endl;
cout << __builtin_popcount(15);
return 0;
}
Java
// java program to demonstrate
// __builtin_popcount()
import java.io.*;
class GFG {
// Driver code
public static void main(String[] args)
{
System.out.println(Integer.bitCount(4));
System.out.println(Integer.bitCount(15));
}
}
// This code is contributed by Raj
Python3
# Python3 program to demonstrate __builtin_popcount()
print(bin(4).count('1'));
print(bin(15).count('1'));
# This code is Contributed by mits
C#
// C# program to demonstrate
// __builtin_popcount()
using System;
using System.Linq;
class GFG {
// Driver code
public static void Main()
{
Console.WriteLine(Convert.ToString(4, 2).Count(c = > c == '1'));
Console.WriteLine(Convert.ToString(15, 2).Count(c = > c == '1'));
}
}
// This code is contributed by mits
PHP
<?php // PHP program to demonstrate // __builtin_popcount() // Driver code $t = log10(4); $x = log(15, 2); $tt = ceil($t); $xx = ceil($x); echo ($tt), "\n"; echo ($xx), "\n"; // This code is contributed // by jit_t ?>
Javascript
<script>
// Javascript program to demonstrate
// __builtin_popcount()
document.write((4).toString(2).split('').
filter(x => x == '1').length + "<br>");
document.write((15).toString(2).split('').
filter(x => x == '1').length);
</script>
Producción :
1 4
4. Asignación de números con el bit. Simplemente mantiene un mapa (o array) de números a bits para un mordisco. Un Nibble contiene 4 bits. Entonces necesitamos una array de hasta 15.
int num_to_bits[16] = {0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4};
Ahora solo necesitamos obtener mordiscos de un largo/int/palabra dado, etc. recursivamente.
C++
// C++ program to count set bits by pre-storing
// count set bits in nibbles.
#include <bits/stdc++.h>
using namespace std;
int num_to_bits[16] = { 0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4 };
/* Recursively get nibble of a given number
and map them in the array */
unsigned int countSetBitsRec(unsigned int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
// Find last nibble
nibble = num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
// Driver code
int main()
{
int num = 31;
cout << countSetBitsRec(num);
return 0;
}
// This code is contributed by rathbhupendra
C
// C program to count set bits by pre-storing
// count set bits in nibbles.
#include <stdio.h>
int num_to_bits[16] = { 0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4 };
/* Recursively get nibble of a given number
and map them in the array */
unsigned int countSetBitsRec(unsigned int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
// Find last nibble
nibble = num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
// Driver code
int main()
{
int num = 31;
printf("%d\n", countSetBitsRec(num));
}
Java
// Java program to count set bits by pre-storing
// count set bits in nibbles.
class GFG {
static int[] num_to_bits = new int[] { 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 };
/* Recursively get nibble of a given number
and map them in the array */
static int countSetBitsRec(int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
// Find last nibble
nibble = num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
// Driver code
public static void main(String[] args)
{
int num = 31;
System.out.println(countSetBitsRec(num));
}
}
// this code is contributed by mits
Python3
# Python3 program to count set bits by pre-storing # count set bits in nibbles. num_to_bits =[0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4]; # Recursively get nibble of a given number # and map them in the array def countSetBitsRec(num): nibble = 0; if(0 == num): return num_to_bits[0]; # Find last nibble nibble = num & 0xf; # Use pre-stored values to find count # in last nibble plus recursively add # remaining nibbles. return num_to_bits[nibble] + countSetBitsRec(num >> 4); # Driver code num = 31; print(countSetBitsRec(num)); # this code is contributed by mits
C#
// C# program to count set bits by pre-storing
// count set bits in nibbles.
class GFG {
static int[] num_to_bits = new int[16] { 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 };
/* Recursively get nibble of a given number
and map them in the array */
static int countSetBitsRec(int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
// Find last nibble
nibble = num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
// Driver code
static void Main()
{
int num = 31;
System.Console.WriteLine(countSetBitsRec(num));
}
}
// this code is contributed by mits
PHP
<?php
// PHP program to count set bits by
// pre-storing count set bits in nibbles.
$num_to_bits = array(0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4);
/* Recursively get nibble of a given
number and map them in the array */
function countSetBitsRec( $num)
{
global $num_to_bits;
$nibble = 0;
if (0 == $num)
return $num_to_bits[0];
// Find last nibble
$nibble = $num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return $num_to_bits[$nibble] +
countSetBitsRec($num >> 4);
}
// Driver code
$num = 31;
echo (countSetBitsRec($num));
// This code is contributed by mits
?>
Javascript
<script>
// Javascript program to count set bits by pre-storing
// count set bits in nibbles.
var num_to_bits =[ 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 ];
/* Recursively get nibble of a given number
and map them in the array */
function countSetBitsRec(num)
{
var nibble = 0;
if (0 == num)
return num_to_bits[0];
// Find last nibble
nibble = num & 0xf;
// Use pre-stored values to find count
// in last nibble plus recursively add
// remaining nibbles.
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
// Driver code
var num = 31;
document.write(countSetBitsRec(num));
// This code is contributed by 29AjayKumar
</script>
Producción :
5
Complejidad temporal: O(log n), porque tenemos log(16, n) niveles de recursividad.
Complejidad de almacenamiento: O(1) Ya sea que el número dado sea corto, int, largo o largo, necesitamos una array de solo 16 tamaños, que es constante.
5. Comprobación de cada bit en un número:
Cada bit en el número se verifica si está configurado o no. El número es AND bit a bit con potencias de 2, por lo que si el resultado no es igual a cero, sabemos que se establece el bit particular en la posición.
C
#include <stdio.h>
// Check each bit in a number is set or not
// and return the total count of the set bits.
int countSetBits(int N)
{
int count = 0;
// (1 << i) = pow(2, i)
for (int i = 0; i < sizeof(int) * 8; i++) {
if (N & (1 << i))
count++;
}
return count;
}
// Driver Code
int main()
{
int N = 15;
printf("%d", countSetBits(N));
return 0;
}
C++
#include <iostream>
using namespace std;
// Check each bit in a number is set or not
// and return the total count of the set bits.
int countSetBits(int N)
{
int count = 0;
// (1 << i) = pow(2, i)
for (int i = 0; i < sizeof(int) * 8; i++) {
if (N & (1 << i))
count++;
}
return count;
}
int main()
{
int N = 15;
cout << countSetBits(N) << endl;
return 0;
}
Java
public class GFG
{
// Check each bit in a number is set or not
// and return the total count of the set bits.
static int countSetBits(int N)
{
int count = 0;
// (1 << i) = pow(2, i)
for (int i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
// Driver code
public static void main(String[] args)
{
int N = 15;
System.out.println(countSetBits(N));
}
}
// This code is contributed by divyeshrabadiya07.
Python3
# Check each bit in a number is set or not # and return the total count of the set bits def countSetBits(N): count = 0 # (1 << i) = pow(2, i) for i in range(4*8): if(N & (1 << i)): count += 1 return count # Driver code N = 15 print(countSetBits(N)) # This code is contributed by avanitrachhadiya2155
C#
using System;
class GFG
{
// Check each bit in a number is set or not
// and return the total count of the set bits.
static int countSetBits(int N)
{
int count = 0;
// (1 << i) = pow(2, i)
for (int i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
// Driver code
static void Main()
{
int N = 15;
Console.WriteLine(countSetBits(N));
}
}
// This code is contributed by divyesh072019.
Javascript
<script>
// Check each bit in a number is set or not
// and return the total count of the set bits.
function countSetBits(N)
{
var count = 0;
// (1 << i) = pow(2, i)
for (i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
// Driver code
var N = 15;
document.write(countSetBits(N));
// This code is contributed by Amit Katiyar
</script>
4
Cuente los bits establecidos en un número entero usando la tabla de búsqueda
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA