Python | Error medio cuadrado

El error cuadrático medio (MSE) o la desviación cuadrática media (MSD) de un estimador mide el promedio de los cuadrados de error, es decir, la diferencia cuadrática promedio entre los valores estimados y el valor verdadero. Es una función de riesgo, correspondiente al valor esperado de la pérdida por error al cuadrado. Siempre es no negativo y los valores cercanos a cero son mejores. El MSE es el segundo momento del error (sobre el origen) y por tanto incorpora tanto la varianza del estimador como su sesgo.

Pasos para encontrar el MSE

Encuentre la ecuación para la línea de regresión.
$\begin{equation*} \hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_i + \hat{\epsilon}_i \end{equation*}$
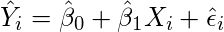
Inserte los valores X en la ecuación encontrada en el paso 1 para obtener los valores Y respectivos, es decir
$\begin{equation*} \hat{Y}_i \end{equation*}$
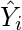
Ahora reste los nuevos valores de Y (es decir, 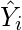$\hat{Y}_i$ ) de los valores de Y originales. Por lo tanto, los valores encontrados son los términos de error. También se conoce como la distancia vertical del punto dado desde la línea de regresión.
$\begin{equation*} Y_i - \hat{Y}_i \end{equation*}$
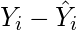
Cuadre los errores encontrados en el paso 3.
$\begin{equation*} {(Y_i - \hat{Y}_i)}^2 \end{equation*}$
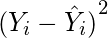
Suma todos los cuadrados.
$\begin{equation*} \sum_{i=1}^{N}(Y_i - \hat{Y}_i)^2 \end{equation*}$
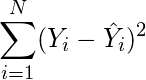
Divida el valor encontrado en el paso 5 por el número total de observaciones.
$\begin{equation*} MSE = \frac{1}{N}\sum_{i=1}^{N}(Y_i - \hat{Y}_i)^2 \end{equation*}$

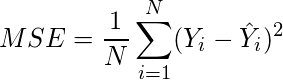
Ejemplo:
Considere los puntos de datos dados: (1,1), (2,1), (3,2), (4,2), (5,4)
Puede usar esta calculadora en línea para encontrar la ecuación / línea de regresión .

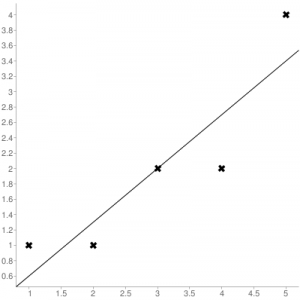
Ecuación de línea de regresión: Y = 0.7X – 0.1

X	Y	$\hat{Y}_i$
1	1	0.6
2	1	1.29
3	2	1.99
4	2	2.69
5	4	3.4

Ahora, usando la fórmula encontrada para MSE en el paso 6 anterior, podemos obtener MSE = 0.21606

MSE usando scikit – aprenda:

from sklearn.metrics import mean_squared_error
  
# Given values
Y_true = [1,1,2,2,4]  # Y_true = Y (original values)
  
# calculated values
Y_pred = [0.6,1.29,1.99,2.69,3.4]  # Y_pred = Y'
  
# Calculation of Mean Squared Error (MSE)
mean_squared_error(Y_true,Y_pred)

Output: 0.21606

MSE usando el módulo Numpy:

import numpy as np
  
# Given values
Y_true = [1,1,2,2,4]  # Y_true = Y (original values)
  
# Calculated values
Y_pred = [0.6,1.29,1.99,2.69,3.4]  # Y_pred = Y'
  
# Mean Squared Error
MSE = np.square(np.subtract(Y_true,Y_pred)).mean()

Output: 0.21606

Publicación traducida automáticamente

Artículo escrito por mkumarchaudhary06 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta