Fórmula de sección para 3 D

Dadas dos coordenadas (x1, y1, z1) y (x2, y2, z2) en 3D, m y n, encuentre las coordenadas que dividen la línea que une (x1, y1, Z1) y (x2, y2, Z2 ) en la razón m : n.

Ejemplos: 

Entrada: x1 = 2, y1 = -1, Z1 = 4, x2 = 4, y2 = 3, Z2 = 2, 
m = 2, n = 3 
Salida: (2.8, .6, 3.2)
Explicación: coordenadas ( 2.8, .6, 3.2) 
divide la línea en razón 2 : 3 
 

Planteamiento: 
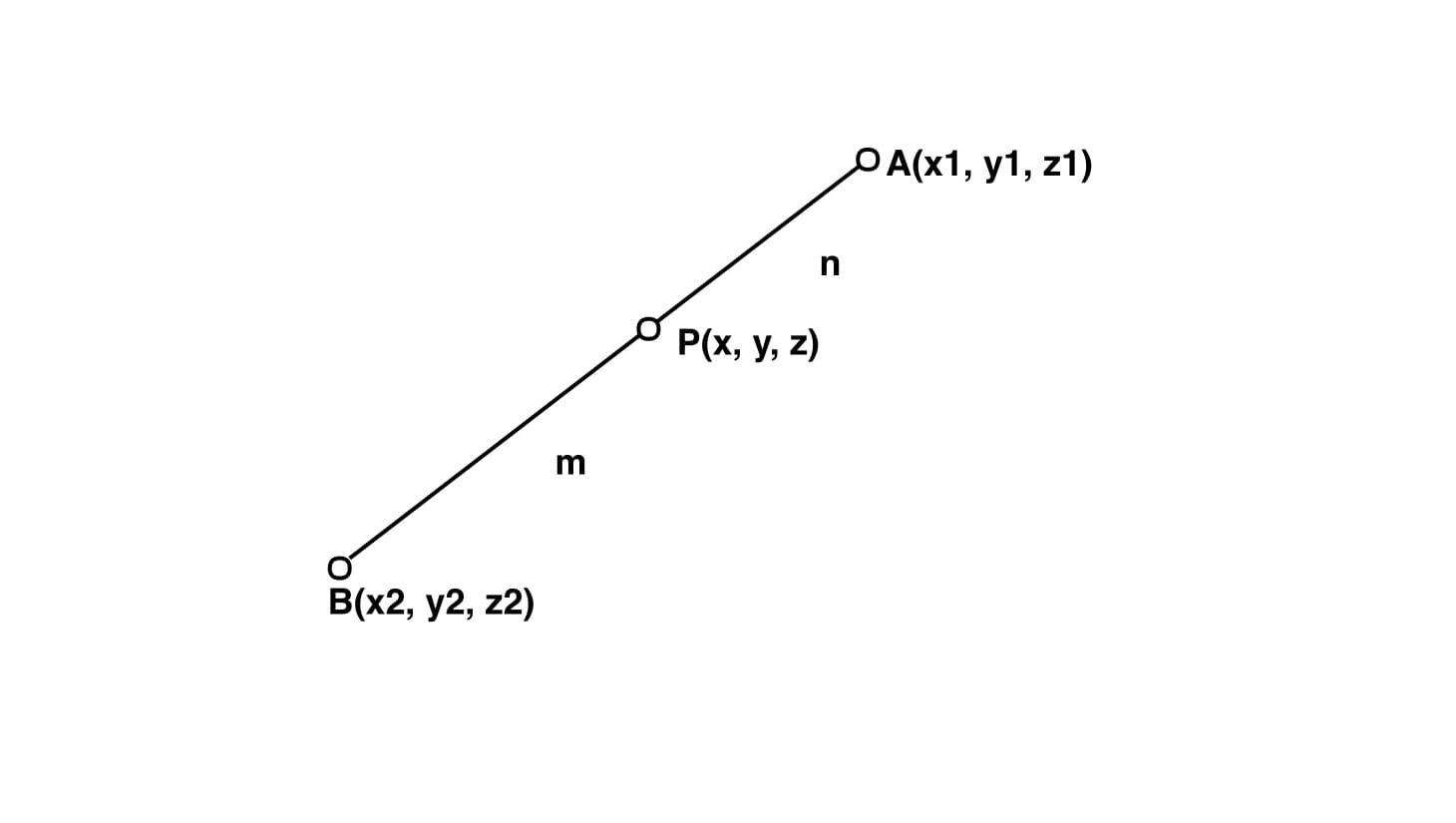
Dadas dos coordenadas A(x1, y1, Z1) y B(x2, y2, Z2) en 3D, m y n, tenemos que encontrar las coordenadas que dividen la línea que une (x1, y1, Z1) y (x2, y2, Z2) en la razón m : n. 
Dejemos que las coordenadas sean P(x, y, z) 
luego de acuerdo con la fórmula de la sección en 3 D 
x = (m * x2 + n * x1) / (m + n) 
y = (m * y2 + n * y1 ) / (m + n) 
z = (m * z2 + n * z1) / (m + n)

A continuación se muestra la implementación del enfoque anterior:  

// CPP program to find point that divides
// given line in given ratio in 3D.
#include <iostream>
using namespace std;
 
// Function to find the section of the line
void section(double x1, double x2, double y1,
             double y2, double z1, double z2,
             double m, double n)
{
    // Applying section formula
    double x = ((m * x2) + (n * x1)) / (m + n);
 
    double y = ((m * y2) + (n * y1)) / (m + n);
 
    double z = ((m * z2) + (n * z1)) / (m + n);
 
    // Printing result
    cout << "(" << x << ", ";
    cout << y << ", ";
    cout << z << ")" << endl;
}
 
// Driver code
int main()
{
    double x1 = 2, x2 = 4, y1 = -1,
           y2 = 3, z1 = 4, z2 = 2,
           m = 2, n = 3;
    section(x1, x2, y1, y2, z1, z2, m, n);
    return 0;
}

// Java program to find point that divides
// given line in given ratio in 3D.
import java.util.*;
 
class solution
{
 
// Function to find the section of the line
static void section(double x1, double x2, double y1,
            double y2, double z1, double z2,
            double m, double n)
{
    // Applying section formula
    double x = ((m * x2) + (n * x1)) / (m + n);
 
    double y = ((m * y2) + (n * y1)) / (m + n);
 
    double z = ((m * z2) + (n * z1)) / (m + n);
 
    System.out.print( "(" +x +", ");
    System.out.print( y+ ", ");
    System.out.println(z + ")" );
 
}
 
// Driver code
public static void main(String arr[])
{
    double x1 = 2, x2 = 4, y1 = -1,
        y2 = 3, z1 = 4, z2 = 2,
        m = 2, n = 3;
    section(x1, x2, y1, y2, z1, z2, m, n);
 
}
 
}
//This code is contributed by Surendra_Gangwar

# Python 3 program to find point that divides
# given line in given ratio in 3D.
 
# Function to find the section of the line
def section(x1, x2, y1, y2, z1, z2, m, n):
    # Applying section formula
    x = ((m * x2) + (n * x1)) / (m + n)
 
    y = ((m * y2) + (n * y1)) / (m + n)
 
    z = ((m * z2) + (n * z1)) / (m + n)
 
    # Printing result
    print("(",x,",",y,",",z,")")
 
# Driver code
if __name__ == '__main__':
    x1 = 2
    x2 = 4
    y1 = -1
    y2 = 3
    z1 = 4
    z2 = 2
    m = 2
    n = 3
    section(x1, x2, y1, y2, z1, z2, m, n)
 
#This code is contributed by
# Surendra_Gangwar

// C# program to find point that divides
// given line in given ratio in 3D.
using System;
 
class GFG
{
     
// Function to find the section
// of the line
static void section(double x1, double x2, double y1,
                    double y2, double z1, double z2,
                    double m, double n)
{
    // Applying section formula
    double x = ((m * x2) + (n * x1)) / (m + n);
 
    double y = ((m * y2) + (n * y1)) / (m + n);
 
    double z = ((m * z2) + (n * z1)) / (m + n);
 
    Console.Write("(" + x +", ");
    Console.Write(y + ", ");
    Console.WriteLine(z + ")" );
}
 
// Driver code
static public void Main ()
{
    double x1 = 2, x2 = 4, y1 = -1,
    y2 = 3, z1 = 4, z2 = 2,
    m = 2, n = 3;
    section(x1, x2, y1, y2, z1, z2, m, n);
}
}
 
// This code is contributed by ajit.

<?php
// PHP program to find point that divides
// given line in given ratio in 3D.
 
// Function to find the section of the line
function section($x1, $x2, $y1,
                 $y2, $z1, $z2,
                 $m, $n)
{
    // Applying section formula
    $x = (($m * $x2) + ($n * $x1)) / ($m + $n);
 
    $y = (($m * $y2) + ($n * $y1)) / ($m + $n);
 
    $z = (($m * $z2) + ($n * $z1)) / ($m + $n);
 
    // Printing result
    echo "(" . $x . ", ";
    echo $y . ", ";
    echo $z . ")" ."\n";
}
 
// Driver code
$x1 = 2; $x2 = 4; $y1 = -1;
$y2 = 3; $z1 = 4; $z2 = 2;
$m = 2; $n = 3;
section($x1, $x2, $y1, $y2,
        $z1, $z2, $m, $n);
 
// This code is contributed
// by Akanksha Rai

<script>
 
// Javascript program to find point that
// divides given line in given ratio in 3D.
 
// Function to find the section
// of the line
function section(x1, x2, y1, y2, z1, z2, m, n)
{
     
    // Applying section formula
    let x = ((m * x2) + (n * x1)) / (m + n);
    let y = ((m * y2) + (n * y1)) / (m + n);
    let z = ((m * z2) + (n * z1)) / (m + n);
 
    document.write("(" + x +", ");
    document.write(y + ", ");
    document.write(z + ")" );
}
 
// Driver code
let x1 = 2, x2 = 4, y1 = -1,
y2 = 3, z1 = 4, z2 = 2,
m = 2, n = 3;
 
section(x1, x2, y1, y2, z1, z2, m, n);
 
// This code is contributed by suresh07
 
</script>

Producción: 

(2.8, 0.6, 3.2)