Máquinas de Moore: una máquina de Moore es básicamente un DFA con una salida asociada con cada estado. Estas máquinas se pueden usar para una amplia variedad de tareas, como contar las ocurrencias de una substring particular en una string dada, encontrar el complemento a 2 de un número binario , etc.
Funcionamiento de la máquina Moore:
- Tiene una salida asociada a cada estado.
- Al tomar entrada, pasa al siguiente estado.
- Al llegar al siguiente estado, imprime la salida del siguiente estado.
- Esto continúa hasta que se alcanza el final de la entrada.
Algunas Aplicaciones de la Máquina Moore
Aplicación 1:
Dada una string S que consta de a y b , y una substring «abb» , la tarea es contar la ocurrencia de la substring dada str en la string dada S utilizando Moore Machines.
Ejemplos:
Entrada: S = “babbbbabb”
Salida:
00010001
ocurrencias: 2
Explicación:
La substring “abb” aparece dos veces en la string dada.
Por lo tanto, para cada substring «abb» se produce un ‘1’.
El número de 1 es 2.
Entrada: S = “ab”
Salida:
000
ocurrencias: 0
Explicación:
No hay ninguna ocurrencia de la substring “abb” en la string dada.
Por lo tanto, el número de 1s es 0.
Enfoque:
La Máquina de Moore requerida para este problema viene dada por:

La tabla de transición para la máquina se proporciona a continuación:

Para implementar esto, cree una estructura para mapear la entrada a su siguiente estado:
struct item
{
int value;
State* next;
};
Luego, incluye esta estructura como un miembro de datos de nuestra clase State . La clase tiene tres miembros de datos:
- Input_1: Esta es una variable de tipo elemento definida anteriormente. Asigna el primer tipo de entrada ‘a’ a su siguiente estado.
- Input_2: Esta también es una variable de tipo elemento. Asigna el segundo tipo de entrada ‘b’ a su siguiente estado.
- m_out: Esta es la salida asociada con cada estado de la Máquina de Moore .
Cada objeto de la clase se comporta como un estado. Toma entrada y va al siguiente estado apropiado. Para pasar al siguiente estado, se puede utilizar un puntero de objeto. Cada objeto también tiene una entrada asociada a él.
Las siguientes funciones miembro se utilizarán para trabajar con estos datos:
- Initialize(): esto inicializa el objeto de clase (estado) con entradas y los siguientes estados correspondientes.
- Transition(): actúa como una tabla de transición para la máquina. Toma un carácter de la string de entrada y lo pasa al estado actual, que luego pasa al siguiente estado apropiado después de producir una salida.
- Traverse(): esta función toma una string de entrada y carácter por carácter la pasa a la función de transición y devuelve la string de salida.
- mooreOut(): Esta función define los estados requeridos (objetos) y los inicializa a los valores requeridos. Luego pasa la string de entrada a la función poligonal y recibe la string de salida.
- countStr(): esta función cuenta las apariciones de 1 en la string de salida y lo devuelve.
El siguiente paso es almacenar el estado actual de la máquina mientras le pasa entradas de string. Esto se puede hacer usando un puntero de objeto estático como miembro de datos de clase :
A continuación se muestra la implementación del enfoque anterior:
C++14
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Define a class named State
class State {
private:
// Item
struct item {
char value;
State* next;
};
// Three states
item Input1;
item Input2;
char m_out;
public:
// Constructor
State()
: Input1{ ' ', nullptr },
Input2{ ' ', nullptr },
m_out{ ' ' }
{
}
// Member functions
static State* m_ptr;
void Initialize(item input1,
item input2,
char out);
static char Transition(char x);
static string Traverse(string& str,
int n);
};
// Global object pointer points to
// current state
State* State::m_ptr{ nullptr };
// Function that initializes the states
// with appropriate values
void State::Initialize(item input1,
item input2,
char out)
{
Input1 = input1;
Input2 = input2;
m_out = out;
}
// Transition function that takes each
// character of string
char State::Transition(char x)
{
char ch{};
// Prints the output
if ((*m_ptr).Input1.value == x) {
// Output the current state
cout << (*m_ptr).m_out;
ch = (*m_ptr).m_out;
// Next input state
m_ptr = (*m_ptr).Input1.next;
}
else {
// Output the current state
cout << (*m_ptr).m_out;
ch = (*m_ptr).m_out;
// Next input state
m_ptr = (*m_ptr).Input2.next;
}
// Return ch
return ch;
}
// Takes the whole string and pass
// it through machine
string State::Traverse(string& str,
int n)
{
string str1{};
// Add all the transition state to
// the string str1
for (int i = 0; i < n; i++)
str1 += Transition(str[i]);
// Append output
str1 += (*m_ptr).m_out;
cout << (*m_ptr).m_out << endl;
// Return str1
return str1;
}
// Function that create states and
// produce output
string mooreOut(string str, int n)
{
State q1, q2, q3, q4;
// Initializing the states
q1.Initialize({ 'a', &q2 },
{ 'b', &q1 }, '0');
q2.Initialize({ 'a', &q2 },
{ 'b', &q3 }, '0');
q3.Initialize({ 'a', &q2 },
{ 'b', &q4 }, '0');
q4.Initialize({ 'a', &q2 },
{ 'b', &q1 }, '1');
State::m_ptr = &q1;
// Traverse the string str1
string str1{ State::Traverse(str, n) };
return str1;
}
// Function that counts the occurrences
// of 1 in the output string
int countStr(string& str, int n)
{
int count{};
// Count the 1s in str
for (int i = 0; i < n; i++) {
if (str[i] == '1')
count++;
}
// Return count
return count;
}
// Driver Code
int main()
{
// Given string
string str{ "babbabbabbb" };
int n{ static_cast<int>(str.length()) };
// Function Call
string str1{ mooreOut(str, n) };
int n1{ static_cast<int>(str.length()) };
// Print the count of substring
cout << "abb occurs " << countStr(str1, n1)
<< " times\n";
return 0;
}
000010010010 abb occurs 3 times
Complejidad de tiempo: O(N)
Espacio auxiliar: O(N)
Aplicación 2:
Dada una string binaria str , la tarea es encontrar el complemento a 2 de la string dada str .
Entrada: str = “111010000”
Salida: 000110000
Entrada: str = “111”
Salida: 001
Enfoque: la idea es comenzar desde el bit más a la derecha y pasarlo a la máquina que da la salida. Pase toda la cuerda así, de derecha a izquierda. Se pueden observar las siguientes observaciones:
Por ejemplo: La string dada es «111010000». Ahora, el complemento a 2 está dado por el complemento a 1 de (str) + 1. Por lo tanto,
str = "111010000"
1s compliment = "000101111"
+ 1
---------------------------
2s complement = 000110000
Aquí podemos observar que desde el bit de más a la derecha se copian los bits de la misma manera hasta que aparece el 1. Después de eso, todos los bits se invierten.
Por lo tanto, la idea es definir una máquina de Moore para comenzar a recibir información del lado derecho. Siempre que el bit sea 0 , da la misma salida (0) . Cuando se encuentra 1 , entonces da 1 para eso. Después de esto, para cualquier bit tomado como entrada, su inverso se da como salida.
La máquina de Moore para este problema se muestra a continuación:
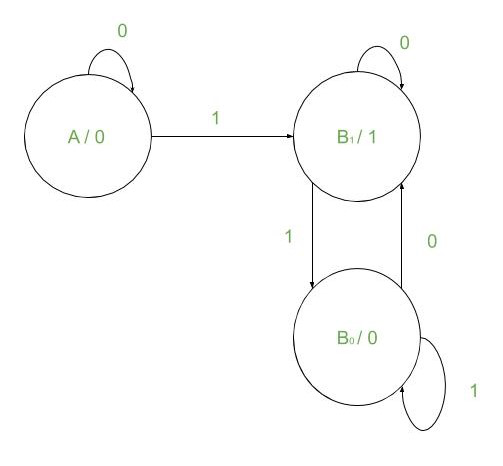
Para implementar esto primero, asigne la tabla de transición para esta máquina. Se necesitan tres estados, es decir, tres objetos de clase Estado definidos al principio:
- Estado1 => Inicializar ({‘0’, &Estado1}, {‘1’, &Estado2}, ‘0’)
- Estado2 => Inicializar ({‘0’, &Estado2}, {‘1’, &Estado3}, ‘1’)
- Estado3 => Inicializar ({‘0’, &Estado2}, {‘1’, &Estado3}, ‘0’)
Después de la inicialización, se necesita una función de transición como la definida anteriormente. Toma una entrada y para eso imprime la salida del estado actual y pasa al siguiente estado asignando la entrada al siguiente estado usando la tabla de transición definida anteriormente. Luego, para atravesar la string, la transición comienza desde el bit más a la derecha y continúa hasta el bit más a la izquierda.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Define a class named State
class State {
private:
struct item {
char value;
State* next;
};
item Input1;
item Input2;
char m_out;
public:
// Constructors
State()
: Input1{ ' ', nullptr },
Input2{ ' ', nullptr },
m_out{ ' ' }
{
}
static State* m_ptr;
// Member Functions
void Initialize(item input1,
item input2,
char out);
static char Transition(char x);
static string Traverse(string& str,
int n);
};
// Global object pointer points to
// current state
State* State::m_ptr{ nullptr };
// Function that initializes the states
// with appropriate values
void State::Initialize(item input1,
item input2,
char out)
{
Input1 = input1;
Input2 = input2;
m_out = out;
}
// Transition function takes each
// character of string
char State::Transition(char x)
{
char ch{};
// Prints the output
if ((*m_ptr).Input1.value == x) {
// Output the current state
cout << (*m_ptr).m_out;
ch = (*m_ptr).m_out;
// Next input state
m_ptr = (*m_ptr).Input1.next;
}
else {
// Output the current state
cout << (*m_ptr).m_out;
ch = (*m_ptr).m_out;
// Next input state
m_ptr = (*m_ptr).Input2.next;
}
// Return ch
return ch;
}
// Takes the whole string and passes
// through machine
string State::Traverse(string& str, int n)
{
string str1{};
// Add all the transition state to
// the string str1
for (int i = n - 1; i >= 0; i--) {
str1 += Transition(str[i]);
}
// To read the characters from end
// therefore we need to reverse
reverse(str1.begin(), str1.end());
return str1;
}
// Function to create states and
// produce output
string mooreOut(string str, int n)
{
State q1, q2, q3;
// Initializing the states
q1.Initialize({ '0', &q1 },
{ '1', &q2 }, '0');
q2.Initialize({ '0', &q2 },
{ '1', &q3 }, '1');
q3.Initialize({ '0', &q2 },
{ '1', &q3 }, '0');
State::m_ptr = &q1;
return State::Traverse(str, n);
}
// Driver Code
int main()
{
// Given string
string str{ "111010000" };
int n{ static_cast<int>(str.length()) };
// Function Call
string str1{ mooreOut(str, n) };
// Print the output
cout << "2's complement: " << str1;
return 0;
}
2's complement: 000110000
Complejidad de tiempo: O(N), donde N es la longitud de la string binaria dada.
Espacio Auxiliar: O(N)