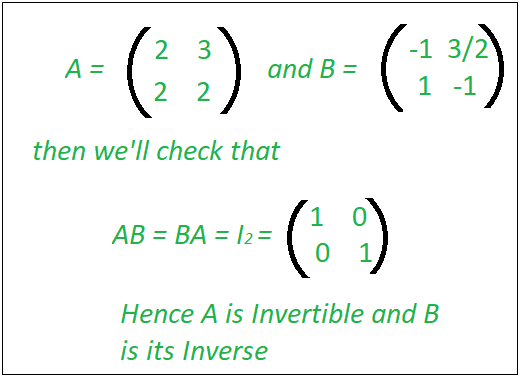
En álgebra lineal, una array cuadrada A de n por n se denomina Invertible, si existe una array cuadrada B de n por n tal que donde ‘ In ‘ denota la array identidad de n por n . La array B se llama array inversa de A. Una array cuadrada es invertible si y solo si su determinante es distinto de cero.![]()
Ejemplos:
Input : {{1, 2, 3}
{4, 5, 6}
{7, 8, 9}}
Output : No
The given matrix is NOT Invertible
The value of Determinant is: 0
Hallamos el determinante de la array . Luego verificamos si el valor del determinante es 0 o no. Si el valor es 0, entonces emitimos, no invertible.
C++
// C++ program to find Determinant of a matrix
#include <bits/stdc++.h>
using namespace std;
// Dimension of input square matrix
#define N 4
// Function to get cofactor of mat[p][q] in temp[][]. n is current
// dimension of mat[][]
void getCofactor(int mat[N][N], int temp[N][N], int p, int q, int n)
{
int i = 0, j = 0;
// Looping for each element of the matrix
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// Copying into temporary matrix only those element
// which are not in given row and column
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
// Row is filled, so increase row index and
// reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
/* Recursive function for finding determinant of matrix.
n is current dimension of mat[][]. */
int determinantOfMatrix(int mat[N][N], int n)
{
int D = 0; // Initialize result
// Base case : if matrix contains single element
if (n == 1)
return mat[0][0];
int temp[N][N]; // To store cofactors
int sign = 1; // To store sign multiplier
// Iterate for each element of first row
for (int f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] * determinantOfMatrix(temp, n - 1);
// terms are to be added with alternate sign
sign = -sign;
}
return D;
}
bool isInvertible(int mat[N][N], int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
// Driver program to test above functions
int main()
{
/* int mat[N][N] = {{6, 1, 1},
{4, -2, 5},
{2, 8, 7}}; */
int mat[N][N] = { { 1, 0, 2, -1 },
{ 3, 0, 0, 5 },
{ 2, 1, 4, -3 },
{ 1, 0, 5, 0 } };
if (isInvertible(mat, N))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// Java program to find
// Determinant of a matrix
class GFG
{
// Dimension of input square matrix
static int N = 4;
// Function to get cofactor
// of mat[p][q] in temp[][].
// n is current dimension
// of mat[][]
static void getCofactor(int [][]mat, int [][]temp,
int p, int q, int n)
{
int i = 0, j = 0;
// Looping for each
// element of the matrix
for (int row = 0; row < n; row++)
{
for (int col = 0; col < n; col++)
{
// Copying into temporary matrix
// only those element which are
// not in given row and column
if (row != p && col != q)
{
temp[i][j++] = mat[row][col];
// Row is filled, so increase
// row index and reset col index
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
/* Recursive function for finding
determinant of matrix. n is current
dimension of mat[][]. */
static int determinantOfMatrix(int [][]mat,
int n)
{
int D = 0; // Initialize result
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
int [][]temp = new int[N][N];
// To store sign multiplier
int sign = 1;
// Iterate for each
// element of first row
for (int f = 0; f < n; f++)
{
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] *
determinantOfMatrix(temp, n - 1);
// terms are to be added
// with alternate sign
sign = -sign;
}
return D;
}
static boolean isInvertible(int [][]mat, int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
// Driver Code
public static void main(String []args)
{
int [][]mat = {{1, 0, 2, -1 },
{3, 0, 0, 5 },
{2, 1, 4, -3 },
{1, 0, 5, 0 }};
if (isInvertible(mat, N))
System.out.println("Yes");
else
System.out.println("No");
}
}
// This code is contributed
// by ChitraNayal
Python 3
# Function to get cofactor of
# mat[p][q] in temp[][]. n is
# current dimension of mat[][]
def getCofactor(mat, temp, p, q, n):
i = 0
j = 0
# Looping for each element
# of the matrix
for row in range(n):
for col in range(n):
# Copying into temporary matrix
# only those element which are
# not in given row and column
if (row != p and col != q) :
temp[i][j] = mat[row][col]
j += 1
# Row is filled, so increase
# row index and reset col index
if (j == n - 1):
j = 0
i += 1
# Recursive function for
# finding determinant of matrix.
# n is current dimension of mat[][].
def determinantOfMatrix(mat, n):
D = 0 # Initialize result
# Base case : if matrix
# contains single element
if (n == 1):
return mat[0][0]
# To store cofactors
temp = [[0 for x in range(N)]
for y in range(N)]
sign = 1 # To store sign multiplier
# Iterate for each
# element of first row
for f in range(n):
# Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n)
D += (sign * mat[0][f] *
determinantOfMatrix(temp, n - 1))
# terms are to be added
# with alternate sign
sign = -sign
return D
def isInvertible(mat, n):
if (determinantOfMatrix(mat, N) != 0):
return True
else:
return False
# Driver Code
mat = [[ 1, 0, 2, -1 ],
[ 3, 0, 0, 5 ],
[ 2, 1, 4, -3 ],
[ 1, 0, 5, 0 ]];
N = 4
if (isInvertible(mat, N)):
print("Yes")
else:
print("No")
# This code is contributed
# by ChitraNayal
C#
// C# program to find
// Determinant of a matrix
using System;
class GFG
{
// Dimension of input
// square matrix
static int N = 4;
// Function to get cofactor of
// mat[p,q] in temp[,]. n is
// current dimension of mat[,]
static void getCofactor(int[,] mat, int[,] temp,
int p, int q, int n)
{
int i = 0, j = 0;
// Looping for each element
// of the matrix
for (int row = 0; row < n; row++)
{
for (int col = 0; col < n; col++)
{
// Copying into temporary matrix
// only those element which are
// not in given row and column
if (row != p && col != q)
{
temp[i, j++] = mat[row, col];
// Row is filled, so
// increase row index and
// reset col index
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
/* Recursive function for finding
determinant of matrix. n is current
dimension of mat[,]. */
static int determinantOfMatrix(int[,]
mat, int n)
{
int D = 0; // Initialize result
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0, 0];
// To store cofactors
int[,] temp = new int[N, N];
int sign = 1; // To store sign multiplier
// Iterate for each
// element of first row
for (int f = 0; f < n; f++)
{
// Getting Cofactor of mat[0,f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0, f] *
determinantOfMatrix(temp, n - 1);
// terms are to be added
// with alternate sign
sign = -sign;
}
return D;
}
static bool isInvertible(int[,] mat, int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
// Driver Code
public static void Main()
{
int[,] mat = {{ 1, 0, 2, -1 },
{ 3, 0, 0, 5 },
{ 2, 1, 4, -3 },
{ 1, 0, 5, 0 }};
if (isInvertible(mat, N))
Console.Write("Yes");
else
Console.Write("No");
}
}
// This code is contributed
// by ChitraNayal
PHP
<?php
// PHP program to find Determinant
// of a matrix
// Dimension of input
// square matrix
$N = 4;
// Function to get cofactor of
// $mat[$p][$q] in $temp[][].
// $n is current dimension of $mat[][]
function getCofactor(&$mat, &$temp,
$p, $q, $n)
{
$i = 0;
$j = 0;
// Looping for each element
// of the matrix
for ($row = 0; $row < $n; $row++)
{
for ($col = 0; $col < $n; $col++)
{
// Copying into temporary matrix
// only those element which are
// not in given row and column
if ($row != $p && $col != $q)
{
$temp[$i][$j++] = $mat[$row][$col];
// Row is filled, so
// increase row index and
// reset col index
if ($j == $n - 1)
{
$j = 0;
$i++;
}
}
}
}
}
/* Recursive function for finding
determinant of matrix. n is current
dimension of $mat[][]. */
function determinantOfMatrix(&$mat, $n)
{
$D = 0; // Initialize result
// Base case : if matrix
// contains single element
if ($n == 1)
return $mat[0][0];
$temp = array(array()); // To store cofactors
$sign = 1; // To store sign multiplier
// Iterate for each
// element of first row
for ($f = 0; $f < $n; $f++)
{
// Getting Cofactor of $mat[0][$f]
getCofactor($mat, $temp, 0, $f, $n);
$D += $sign * $mat[0][$f] *
determinantOfMatrix($temp, $n - 1);
// terms are to be added
// with alternate sign
$sign = -$sign;
}
return $D;
}
function isInvertible(&$mat, $n)
{
global $N;
if (determinantOfMatrix($mat, $N) != 0)
return true;
else
return false;
}
// Driver Code
$mat = array(array(1, 0, 2, -1 ),
array(3, 0, 0, 5 ),
array(2, 1, 4, -3 ),
array(1, 0, 5, 0 ));
if (isInvertible($mat, $N))
echo "Yes";
else
echo "No";
// This code is contributed
// by ChitraNayal
?>
Javascript
<script>
// Javascript program to find
// Determinant of a matrix
// Function to get cofactor
// of mat[p][q] in temp[][].
// n is current dimension
// of mat[][]
function getCofactor(mat,temp,p,q,n)
{
let i = 0, j = 0;
// Looping for each
// element of the matrix
for (let row = 0; row < n; row++)
{
for (let col = 0; col < n; col++)
{
// Copying into temporary matrix
// only those element which are
// not in given row and column
if (row != p && col != q)
{
temp[i][j++] = mat[row][col];
// Row is filled, so increase
// row index and reset col index
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
/* Recursive function for finding
determinant of matrix. n is current
dimension of mat[][]. */
function determinantOfMatrix(mat,n)
{
let D = 0; // Initialize result
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
let temp = new Array(N);
for(let i=0;i<N;i++)
{
temp[i]=new Array(N);
for(let j=0;j<N;j++)
{
temp[i][j]=0;
}
}
// To store sign multiplier
let sign = 1;
// Iterate for each
// element of first row
for (let f = 0; f < n; f++)
{
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] *
determinantOfMatrix(temp, n - 1);
// terms are to be added
// with alternate sign
sign = -sign;
}
return D;
}
function isInvertible(mat,n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
// Driver Code
let mat = [[ 1, 0, 2, -1 ],
[ 3, 0, 0, 5 ],
[ 2, 1, 4, -3 ],
[ 1, 0, 5, 0 ]];
let N = 4
if (isInvertible(mat, N))
document.write("Yes")
else
document.write("No")
// This code is contributed by rag2127
</script>
Producción:
Yes
Publicación traducida automáticamente
Artículo escrito por AmanSrivastava1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA