Nos dan tres valores ![]() ,
, ![]() y
y ![]() donde
donde ![]() es el número de filas en la array,
es el número de filas en la array, ![]() es el número de columnas en la array y
es el número de columnas en la array y ![]() es el número que puede tener solo dos valores -1 y 1. Nuestro objetivo es encontrar el número de formas de llenar la array de
es el número que puede tener solo dos valores -1 y 1. Nuestro objetivo es encontrar el número de formas de llenar la array de ![]() tal que el producto de todos los elementos de cada fila y cada columna sea igual a
tal que el producto de todos los elementos de cada fila y cada columna sea igual a ![]() . Dado que el número de formas puede ser grande, generaremos
. Dado que el número de formas puede ser grande, generaremos ![]()
Ejemplos:
Input : n = 2, m = 4, k = -1 Output : 8 Following configurations satisfy the conditions:-


Input : n = 2, m = 1, k = -1
Output : The number of filling the matrix
are 0
De las condiciones anteriores, está claro que los únicos elementos que se pueden ingresar en la array son 1 y -1. Ahora podemos deducir fácilmente algunos de los casos de esquina
- Si k = -1, entonces la suma del número de filas y columnas no puede ser impar porque -1 estará presente un
número impar de veces en cada fila y columna, por lo tanto, si la suma es impar, la respuesta es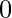 .
. - Si n = 1 o m = 1, solo hay una forma de llenar la array, por lo tanto, la respuesta es 1.
- Si ninguno de los casos anteriores es aplicable, llenamos las primeras
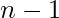 filas y las primeras
filas y las primeras 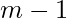 columnas con 1 y -1. Luego, los números restantes se pueden identificar de manera única ya que el producto de cada fila y cada columna ya se conoce, por lo tanto, la respuesta es
columnas con 1 y -1. Luego, los números restantes se pueden identificar de manera única ya que el producto de cada fila y cada columna ya se conoce, por lo tanto, la respuesta es 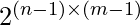 .
.
Implementación:
C++
// CPP program to find number of ways to fill
// a matrix under given constraints
#include <bits/stdc++.h>
using namespace std;
#define mod 100000007
/* Returns a raised power t under modulo mod */
long long modPower(long long a, long long t)
{
long long now = a, ret = 1;
// Counting number of ways of filling the matrix
while (t) {
if (t & 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
// Function calculating the answer
long countWays(int n, int m, int k)
{
// if sum of numbers of rows and columns is odd
// i.e (n + m) % 2 == 1 and k = -1 then there
// are 0 ways of filiing the matrix.
if (k == -1 && (n + m) % 2 == 1)
return 0;
// If there is one row or one column then there
// is only one way of filling the matrix
if (n == 1 || m == 1)
return 1;
// If the above cases are not followed then we
// find ways to fill the n - 1 rows and m - 1
// columns which is 2 ^ ((m-1)*(n-1)).
return (modPower(modPower((long long)2, n - 1),
m - 1) % mod);
}
// Driver function for the program
int main()
{
int n = 2, m = 7, k = 1;
cout << countWays(n, m, k);
return 0;
}
Java
// Java program to find number of ways to fill
// a matrix under given constraints
import java.io.*;
class Example {
final static long mod = 100000007;
/* Returns a raised power t under modulo mod */
static long modPower(long a, long t, long mod)
{
long now = a, ret = 1;
// Counting number of ways of filling the
// matrix
while (t > 0) {
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
// Function calculating the answer
static long countWays(int n, int m, int k)
{
// if sum of numbers of rows and columns is
// odd i.e (n + m) % 2 == 1 and k = -1,
// then there are 0 ways of filiing the matrix.
if (n == 1 || m == 1)
return 1;
// If there is one row or one column then
// there is only one way of filling the matrix
else if ((n + m) % 2 == 1 && k == -1)
return 0;
// If the above cases are not followed then we
// find ways to fill the n - 1 rows and m - 1
// columns which is 2 ^ ((m-1)*(n-1)).
return (modPower(modPower((long)2, n - 1, mod),
m - 1, mod) % mod);
}
// Driver function for the program
public static void main(String args[]) throws IOException
{
int n = 2, m = 7, k = 1;
System.out.println(countWays(n, m, k));
}
}
Python3
# Python program to find number of ways to # fill a matrix under given constraints # Returns a raised power t under modulo mod def modPower(a, t): now = a; ret = 1; mod = 100000007; # Counting number of ways of filling # the matrix while (t): if (t & 1): ret = now * (ret % mod); now = now * (now % mod); t >>= 1; return ret; # Function calculating the answer def countWays(n, m, k): mod= 100000007; # if sum of numbers of rows and columns # is odd i.e (n + m) % 2 == 1 and k = -1 # then there are 0 ways of filiing the matrix. if (k == -1 and ((n + m) % 2 == 1)): return 0; # If there is one row or one column then # there is only one way of filling the matrix if (n == 1 or m == 1): return 1; # If the above cases are not followed then we # find ways to fill the n - 1 rows and m - 1 # columns which is 2 ^ ((m-1)*(n-1)). return (modPower(modPower(2, n - 1), m - 1) % mod); # Driver Code n = 2; m = 7; k = 1; print(countWays(n, m, k)); # This code is contributed # by Shivi_Aggarwal
C#
// C# program to find number of ways to fill
// a matrix under given constraints
using System;
class Example
{
static long mod = 100000007;
// Returns a raised power t
// under modulo mod
static long modPower(long a, long t,
long mod)
{
long now = a, ret = 1;
// Counting number of ways
// of filling the
// matrix
while (t > 0)
{
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
// Function calculating the answer
static long countWays(int n, int m,
int k)
{
// if sum of numbers of rows
// and columns is odd i.e
// (n + m) % 2 == 1 and
// k = -1, then there are 0
// ways of filiing the matrix.
if (n == 1 || m == 1)
return 1;
// If there is one row or one
// column then there is only
// one way of filling the matrix
else if ((n + m) % 2 == 1 && k == -1)
return 0;
// If the above cases are not
// followed then we find ways
// to fill the n - 1 rows and
// m - 1 columns which is
// 2 ^ ((m-1)*(n-1)).
return (modPower(modPower((long)2, n - 1,
mod), m - 1, mod) % mod);
}
// Driver Code
public static void Main()
{
int n = 2, m = 7, k = 1;
Console.WriteLine(countWays(n, m, k));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find number
// of ways to fill a matrix under
// given constraints
$mod = 100000007;
// Returns a raised power t
// under modulo mod
function modPower($a, $t)
{
global $mod;
$now = $a; $ret = 1;
// Counting number of ways
// of filling the matrix
while ($t)
{
if ($t & 1)
$ret = $now * ($ret % $mod);
$now = $now * ($now % $mod);
$t >>= 1;
}
return $ret;
}
// Function calculating the answer
function countWays($n, $m, $k)
{
global $mod;
// if sum of numbers of rows
// and columns is odd i.e
// (n + m) % 2 == 1 and k = -1
// then there are 0 ways of
// filiing the matrix.
if ($k == -1 and ($n + $m) % 2 == 1)
return 0;
// If there is one row or
// one column then there
// is only one way of
// filling the matrix
if ($n == 1 or $m == 1)
return 1;
// If the above cases are
// not followed then we
// find ways to fill the
// n - 1 rows and m - 1
// columns which is
// 2 ^ ((m-1)*(n-1)).
return (modPower(modPower(2, $n - 1),
$m - 1) % $mod);
}
// Driver Code
$n = 2;
$m = 7;
$k = 1;
echo countWays($n, $m, $k);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// JavaScript program to find number of
// ways to fill a matrix under given
// constraints
let mod = 100000007;
// Returns a raised power t under modulo mod
function modPower(a, t, mod)
{
let now = a, ret = 1;
// Counting number of ways of
// filling the matrix
while (t > 0)
{
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
// Function calculating the answer
function countWays(n, m, k)
{
// If sum of numbers of rows and columns is
// odd i.e (n + m) % 2 == 1 and k = -1,
// then there are 0 ways of filiing the matrix.
if (n == 1 || m == 1)
return 1;
// If there is one row or one column then
// there is only one way of filling the matrix
else if ((n + m) % 2 == 1 && k == -1)
return 0;
// If the above cases are not followed then we
// find ways to fill the n - 1 rows and m - 1
// columns which is 2 ^ ((m-1)*(n-1)).
return (modPower(modPower(2, n - 1, mod),
m - 1, mod) % mod);
}
// Driver Code
let n = 2, m = 7, k = 1;
document.write(countWays(n, m, k));
// This code is contributed by code_hunt
</script>
Producción:
64
Complejidad del tiempo:
*** QuickLaTeX cannot compile formula: *** Error message: Error: Nothing to show, formula is empty
.
Complejidad espacial: O(1).