Programa para array de Markov

Dada la array 2D amxn, verifique si es una array de Markov.
Array de Markov: La array en la que la suma de cada fila es igual a 1.
 

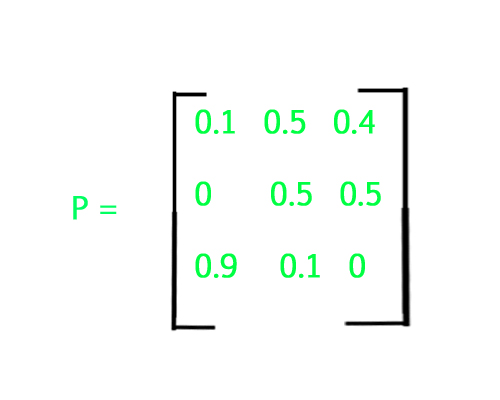
Ejemplo de array de Markov

Ejemplos: 
 

Input :
1    0   0
0.5  0  0.5
0    0   1
Output : yes

Explanation :
Sum of each row results to 1, 
therefore it is a Markov Matrix.

Input :
1 0 0
0 0 2
1 0 0
Output :
no

Enfoque: inicialice una array 2D, luego tome otra array unidimensional para almacenar la suma de cada fila de la array y verifique si toda la suma almacenada en esta array 1D es igual a 1, en caso afirmativo, entonces es array de Markov de lo contrario. 
 

// C++ code to check Markov Matrix
#include <iostream>
using namespace std;
 
#define n 3
 
bool checkMarkov(double m[][n])
{
    // outer loop to access rows
    // and inner to access columns
    for (int i = 0; i <n; i++) {
 
        // Find sum of current row
        double sum = 0;
        for (int j = 0; j < n; j++)
            sum = sum + m[i][j];
 
        if (sum != 1)
        return false;
    }
 
    return true;
}
 
// Driver Code
int main()
{
    // Matrix to check
    double m[3][3] = { { 0, 0, 1 },
                    { 0.5, 0, 0.5 },
                    { 1, 0, 0 } };
 
    // calls the function check()
    if (checkMarkov(m))
        cout << " yes ";
    else
        cout << " no ";
}
 
// This code is contributed by Anant Agarwal.

// Java code to check Markov Matrix
import java.io.*;
 
public class markov
{
    static boolean checkMarkov(double m[][])
    {
        // outer loop to access rows
        // and inner to access columns
        for (int i = 0; i < m.length; i++) {
 
            // Find sum of current row
            double sum = 0;
            for (int j = 0; j < m[i].length; j++)
                sum = sum + m[i][j];
 
            if (sum != 1)
               return false;
        }
 
        return true;
    }
 
    public static void main(String args[])
    {
        // Matrix to check
        double m[][] = { { 0, 0, 1 },
                         { 0.5, 0, 0.5 },
                         { 1, 0, 0 } };
 
        // calls the function check()
        if (checkMarkov(m))
            System.out.println(" yes ");
        else
            System.out.println(" no ");
    }
}

# Python 3 code to check Markov Matrix
 
def checkMarkov(m) :
     
    # Outer loop to access rows
    # and inner to access columns
    for i in range(0, len(m)) :
         
        # Find sum of current row
        sm = 0
        for j in range(0, len(m[i])) :
            sm = sm + m[i][j]
 
        if (sm != 1) :
            return False
             
    return True
     
# Matrix to check
m = [ [ 0, 0, 1 ],
      [ 0.5, 0, 0.5 ],
      [ 1, 0, 0 ]      ]
 
# Calls the function check()
if (checkMarkov(m)) :
    print(" yes ")
else :
    print(" no ")
     
     
# This code is contributed by Nikita Tiwari.

// C# code to check
// Markov Matrix
using System;
 
class GFG
{
static bool checkMarkov(double [,]m)
{
    // outer loop to access
    // rows and inner to
    // access columns
    for (int i = 0;
             i < m.GetLength(0); i++)
    {
 
        // Find sum of
        // current row
        double sum = 0;
        for (int j = 0;
                 j < m.GetLength(1); j++)
            sum = sum + m[i, j];
 
        if (sum != 1)
        return false;
    }
 
    return true;
}
 
// Driver Code
static void Main()
{
    // Matrix to check
    double [,]m = new double[,]{{ 0, 0, 1},
                                {0.5, 0, 0.5},
                                {1, 0, 0}};
 
    // calls the
    // function check()
    if (checkMarkov(m))
        Console.WriteLine(" yes ");
    else
        Console.WriteLine(" no ");
}
}
 
// This code is contributed by
// Manish Shaw(manishshaw1)

<?php
// PHP code to check Markov Matrix
 
function checkMarkov($m)
{
    $n = 3;
     
    // outer loop to access rows
    // and inner to access columns
    for ($i = 0; $i <$n; $i++)
    {
 
        // Find sum of current row
        $sum = 0;
        for ($j = 0; $j < $n; $j++)
            $sum = $sum + $m[$i][$j];
 
        if ($sum != 1)
        return false;
    }
 
    return true;
}
 
    // Driver Code
    // Matrix to check
    $m = array(array(0, 0, 1),
               array(0.5, 0, 0.5),
               array(1, 0, 0));
 
 
    // calls the function check()
    if (checkMarkov($m))
        echo " yes ";
    else
        echo " no ";
 
// This code is contributed by nitin mittal.
?>

<script>
 
// Javascript code to check Markov Matrix
 
 
let n = 3
 
function checkMarkov( m)
{
    // outer loop to access rows
    // and inner to access columns
    for (let i = 0; i <n; i++) {
 
        // Find sum of current row
        let sum = 0;
        for (let j = 0; j < n; j++)
            sum = sum + m[i][j];
 
        if (sum != 1)
        return false;
    }
 
    return true;
}
 
 
    // driver code
 
    // Matrix to check
    let m = [ [ 0, 0, 1 ],
            [ 0.5, 0, 0.5 ],
            [ 1, 0, 0 ] ];
 
    // calls the function check()
    if (checkMarkov(m))
        document.write(" yes ");
    else
       document.write(" no ");
     
</script>

Producción : 

yes

Tiempo Complejidad: O(n ² )
Espacio Auxiliar: O(1)