Dada una array N x N, encuentre la subarray akxk donde k <= N y k >= 1, tal que la suma de todos los elementos en la subarray sea máxima. La array de entrada puede contener números cero, positivos y negativos.
Por ejemplo, considere la siguiente array, si k = 3, entonces la salida debe imprimir la subarray encerrada en azul.
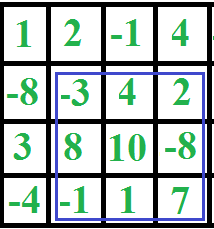
Le recomendamos encarecidamente que minimice su navegador y que pruebe esto usted mismo primero.
Una solución simple es considerar todos los subcuadrados posibles de tamaño kxk en nuestra array de entrada y encontrar el que tenga la suma máxima. La complejidad temporal de la solución anterior es O(N 2 k 2 ).
Podemos resolver este problema en tiempo O(N 2 ). Este problema es principalmente una extensión de esteproblema de imprimir todas las sumas. La idea es preprocesar la array cuadrada dada. En el paso de preprocesamiento, calcule la suma de todas las franjas verticales de tamaño kx 1 en una array cuadrada temporal stripSum[][]. Una vez que tenemos la suma de todas las tiras verticales, podemos calcular la suma del primer subcuadrado en una fila como la suma de las primeras k tiras en esa fila, y para los subcuadrados restantes, podemos calcular la suma en tiempo O(1) eliminando la franja más a la izquierda del subcuadrado anterior y agregando la franja más a la derecha del nuevo cuadrado.
A continuación se muestra la implementación de la idea anterior.
C++
// An efficient C++ program to find maximum sum sub-square
// matrix
#include <bits/stdc++.h>
using namespace std;
// Size of given matrix
#define N 5
// A O(n^2) function to the maximum sum sub-squares of size
// k x k in a given square matrix of size n x n
void printMaxSumSub(int mat[][N], int k)
{
// k must be smaller than or equal to n
if (k > N)
return;
// 1: PREPROCESSING
// To store sums of all strips of size k x 1
int stripSum[N][N];
// Go column by column
for (int j = 0; j < N; j++) {
// Calculate sum of first k x 1 rectangle in this
// column
int sum = 0;
for (int i = 0; i < k; i++)
sum += mat[i][j];
stripSum[0][j] = sum;
// Calculate sum of remaining rectangles
for (int i = 1; i < N - k + 1; i++) {
sum += (mat[i + k - 1][j] - mat[i - 1][j]);
stripSum[i][j] = sum;
}
}
// max_sum stores maximum sum and its position in matrix
int max_sum = INT_MIN, *pos = NULL;
// 2: CALCULATE SUM of Sub-Squares using stripSum[][]
for (int i = 0; i < N - k + 1; i++) {
// Calculate and print sum of first subsquare in
// this row
int sum = 0;
for (int j = 0; j < k; j++)
sum += stripSum[i][j];
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos = &(mat[i][0]);
}
// Calculate sum of remaining squares in current row
// by removing the leftmost strip of previous
// sub-square and adding a new strip
for (int j = 1; j < N - k + 1; j++) {
sum += (stripSum[i][j + k - 1]
- stripSum[i][j - 1]);
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos = &(mat[i][j]);
}
}
}
// Print the result matrix
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++)
cout << *(pos + i * N + j) << " ";
cout << endl;
}
}
// Driver program to test above function
int main()
{
int mat[N][N] = {
{ 1, 1, 1, 1, 1 }, { 2, 2, 2, 2, 2 },
{ 3, 8, 6, 7, 3 }, { 4, 4, 4, 4, 4 },
{ 5, 5, 5, 5, 5 },
};
int k = 3;
cout << "Maximum sum 3 x 3 matrix is\n";
printMaxSumSub(mat, k);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// An efficient C program to find maximum sum sub-square
// matrix
#include <limits.h>
#include <stdio.h>
// Size of given matrix
#define N 5
// A O(n^2) function to the maximum sum sub-squares of size
// k x k in a given square matrix of size n x n
void printMaxSumSub(int mat[][N], int k)
{
// k must be smaller than or equal to n
if (k > N)
return;
// 1: PREPROCESSING
// To store sums of all strips of size k x 1
int stripSum[N][N];
// Go column by column
for (int j = 0; j < N; j++) {
// Calculate sum of first k x 1 rectangle in this
// column
int sum = 0;
for (int i = 0; i < k; i++)
sum += mat[i][j];
stripSum[0][j] = sum;
// Calculate sum of remaining rectangles
for (int i = 1; i < N - k + 1; i++) {
sum += (mat[i + k - 1][j] - mat[i - 1][j]);
stripSum[i][j] = sum;
}
}
// max_sum stores maximum sum and its position in matrix
int max_sum = INT_MIN, *pos = NULL;
// 2: CALCULATE SUM of Sub-Squares using stripSum[][]
for (int i = 0; i < N - k + 1; i++) {
// Calculate and print sum of first subsquare in
// this row
int sum = 0;
for (int j = 0; j < k; j++)
sum += stripSum[i][j];
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos = &(mat[i][0]);
}
// Calculate sum of remaining squares in current row
// by removing the leftmost strip of previous
// sub-square and adding a new strip
for (int j = 1; j < N - k + 1; j++) {
sum += (stripSum[i][j + k - 1]
- stripSum[i][j - 1]);
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos = &(mat[i][j]);
}
}
}
// Print the result matrix
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++)
printf("%d ", *(pos + i * N + j));
printf("\n");
}
}
// Driver program to test above function
int main()
{
int mat[N][N] = {
{ 1, 1, 1, 1, 1 }, { 2, 2, 2, 2, 2 },
{ 3, 8, 6, 7, 3 }, { 4, 4, 4, 4, 4 },
{ 5, 5, 5, 5, 5 },
};
int k = 3;
printf("Maximum sum 3 x 3 matrix is\n");
printMaxSumSub(mat, k);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// An efficient Java program to find maximum sum
// sub-square matrix
// Class to store the position of start of
// maximum sum in matrix
class Position {
int x;
int y;
// Constructor
Position(int x, int y)
{
this.x = x;
this.y = y;
}
// Updates the position if new maximum sum
// is found
void updatePosition(int x, int y)
{
this.x = x;
this.y = y;
}
// returns the current value of X
int getXPosition() { return this.x; }
// returns the current value of y
int getYPosition() { return this.y; }
}
class Gfg {
// Size of given matrix
static int N;
// A O(n^2) function to the maximum sum sub-
// squares of size k x k in a given square
// matrix of size n x n
static void printMaxSumSub(int[][] mat, int k)
{
// k must be smaller than or equal to n
if (k > N)
return;
// 1: PREPROCESSING
// To store sums of all strips of size k x 1
int[][] stripSum = new int[N][N];
// Go column by column
for (int j = 0; j < N; j++) {
// Calculate sum of first k x 1 rectangle
// in this column
int sum = 0;
for (int i = 0; i < k; i++)
sum += mat[i][j];
stripSum[0][j] = sum;
// Calculate sum of remaining rectangles
for (int i = 1; i < N - k + 1; i++) {
sum += (mat[i + k - 1][j] - mat[i - 1][j]);
stripSum[i][j] = sum;
}
}
// max_sum stores maximum sum and its
// position in matrix
int max_sum = Integer.MIN_VALUE;
Position pos = new Position(-1, -1);
// 2: CALCULATE SUM of Sub-Squares using
// stripSum[][]
for (int i = 0; i < N - k + 1; i++) {
// Calculate and print sum of first subsquare
// in this row
int sum = 0;
for (int j = 0; j < k; j++)
sum += stripSum[i][j];
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos.updatePosition(i, 0);
}
// Calculate sum of remaining squares in
// current row by removing the leftmost
// strip of previous sub-square and adding
// a new strip
for (int j = 1; j < N - k + 1; j++) {
sum += (stripSum[i][j + k - 1] - stripSum[i][j - 1]);
// Update max_sum and position of result
if (sum > max_sum) {
max_sum = sum;
pos.updatePosition(i, j);
}
}
}
// Print the result matrix
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++)
System.out.print(mat[i + pos.getXPosition()][j + pos.getYPosition()]
+ " ");
System.out.println();
}
}
// Driver program to test above function
public static void main(String[] args)
{
N = 5;
int[][] mat = { { 1, 1, 1, 1, 1 },
{ 2, 2, 2, 2, 2 },
{ 3, 8, 6, 7, 3 },
{ 4, 4, 4, 4, 4 },
{ 5, 5, 5, 5, 5 } };
int k = 3;
System.out.println("Maximum sum 3 x 3 matrix is");
printMaxSumSub(mat, k);
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# An efficient Python3 program to find maximum sum
# sub-square matrix
# Size of given matrix
N = 5
# A O(n^2) function to the maximum sum sub-
# squares of size k x k in a given square
# matrix of size n x n
def printMaxSumSub(mat, k):
# k must be smaller than or equal to n
if (k > N):
return;
# 1: PREPROCESSING
# To store sums of all strips of size k x 1
stripSum = [[0 for j in range(N)] for i in range(N)];
# Go column by column
for j in range(N):
# Calculate sum of first k x 1 rectangle
# in this column
sum = 0;
for i in range(k):
sum += mat[i][j];
stripSum[0][j] = sum;
# Calculate sum of remaining rectangles
for i in range(1,N-k+1):
sum += (mat[i+k-1][j] - mat[i-1][j]);
stripSum[i][j] = sum;
# max_sum stores maximum sum and its
# position in matrix
max_sum = -1000000000
i_ind = 0
j_ind = 0
# 2: CALCULATE SUM of Sub-Squares using stripSum[][]
for i in range(N-k+1):
# Calculate and print sum of first subsquare
# in this row
sum = 0;
for j in range(k):
sum += stripSum[i][j];
# Update max_sum and position of result
if (sum > max_sum):
max_sum = sum;
i_ind = i
j_ind = 0
# Calculate sum of remaining squares in
# current row by removing the leftmost
# strip of previous sub-square and adding
# a new strip
for j in range(1,N-k+1):
sum += (stripSum[i][j+k-1] - stripSum[i][j-1]);
# Update max_sum and position of result
if (sum > max_sum):
max_sum = sum;
i_ind = i
j_ind = j
# Print the result matrix
for i in range(k):
for j in range(k):
print(mat[i+i_ind][j+j_ind], end = ' ')
print()
# Driver program to test above function
mat = [[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2],
[3, 8, 6, 7, 3],
[4, 4, 4, 4, 4],
[5, 5, 5, 5, 5],
];
k = 3;
print("Maximum sum 3 x 3 matrix is");
printMaxSumSub(mat, k);
# This code is contributed by rutvik_56.
C#
// An efficient C# program to find maximum sum
// sub-square matrix
using System;
// Class to store the position of start of
// maximum sum in matrix
class Position
{
int x;
int y;
// Constructor
public Position(int x, int y)
{
this.x = x;
this.y = y;
}
// Updates the position if new maximum sum
// is found
public void updatePosition(int x, int y)
{
this.x = x;
this.y = y;
}
// returns the current value of X
public int getXPosition()
{
return this.x;
}
// returns the current value of y
public int getYPosition()
{
return this.y;
}
}
class GFG
{
// Size of given matrix
static int N;
// A O(n^2) function to the maximum sum sub-
// squares of size k x k in a given square
// matrix of size n x n
static void printMaxSumSub(int[,] mat, int k)
{
// k must be smaller than or equal to n
if (k > N)
return;
// 1: PREPROCESSING
// To store sums of all strips of size k x 1
int[,] stripSum = new int[N, N];
// Go column by column
for (int j = 0; j < N; j++)
{
// Calculate sum of first k x 1 rectangle
// in this column
int sum = 0;
for (int i = 0; i < k; i++)
sum += mat[i, j];
stripSum[0, j] = sum;
// Calculate sum of remaining rectangles
for (int i = 1; i < N - k + 1; i++)
{
sum += (mat[i + k - 1, j] -
mat[i - 1, j]);
stripSum[i, j] = sum;
}
}
// max_sum stores maximum sum and its
// position in matrix
int max_sum = int.MinValue;
Position pos = new Position(-1, -1);
// 2: CALCULATE SUM of Sub-Squares using stripSum[,]
for (int i = 0; i < N - k + 1; i++)
{
// Calculate and print sum of first subsquare
// in this row
int sum = 0;
for (int j = 0; j < k; j++)
sum += stripSum[i, j];
// Update max_sum and position of result
if (sum > max_sum)
{
max_sum = sum;
pos.updatePosition(i, 0);
}
// Calculate sum of remaining squares in
// current row by removing the leftmost
// strip of previous sub-square and adding
// a new strip
for (int j = 1; j < N - k + 1; j++)
{
sum += (stripSum[i, j + k - 1] -
stripSum[i, j - 1]);
// Update max_sum and position of result
if (sum > max_sum)
{
max_sum = sum;
pos.updatePosition(i, j);
}
}
}
// Print the result matrix
for (int i = 0; i < k; i++)
{
for (int j = 0; j < k; j++)
{
Console.Write(mat[i + pos.getXPosition(),
j + pos.getYPosition()] + " ");
}
Console.WriteLine();
}
}
// Driver Code
public static void Main(String[] args)
{
N = 5;
int[,] mat = {{ 1, 1, 1, 1, 1 },
{ 2, 2, 2, 2, 2 },
{ 3, 8, 6, 7, 3 },
{ 4, 4, 4, 4, 4 },
{ 5, 5, 5, 5, 5 }};
int k = 3;
Console.WriteLine("Maximum sum 3 x 3 matrix is");
printMaxSumSub(mat, k);
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// An efficient Javascript program to find maximum sum
// sub-square matrix
// Class to store the position of start of
// maximum sum in matrix
class Position
{
constructor()
{
this.x = 0;
this.y = 0;
}
// Constructor
Position(x, y)
{
this.x = x;
this.y = y;
}
// Updates the position if new maximum sum
// is found
updatePosition(x, y)
{
this.x = x;
this.y = y;
}
// returns the current value of X
getXPosition()
{
return this.x;
}
// returns the current value of y
getYPosition()
{
return this.y;
}
}
// Size of given matrix
var N = 0;
// A O(n^2) function to the maximum sum sub-
// squares of size k x k in a given square
// matrix of size n x n
function printMaxSumSub(mat, k)
{
// k must be smaller than or equal to n
if (k > N)
return;
// 1: PREPROCESSING
// To store sums of all strips of size k x 1
var stripSum = Array.from(Array(N), ()=>Array(N));
// Go column by column
for (var j = 0; j < N; j++)
{
// Calculate sum of first k x 1 rectangle
// in this column
var sum = 0;
for (var i = 0; i < k; i++)
sum += mat[i][j];
stripSum[0][j] = sum;
// Calculate sum of remaining rectangles
for (var i = 1; i < N - k + 1; i++)
{
sum += (mat[i + k - 1][j] -
mat[i - 1][j]);
stripSum[i][j] = sum;
}
}
// max_sum stores maximum sum and its
// position in matrix
var max_sum = -1000000000;
var pos = new Position(-1, -1);
// 2: CALCULATE SUM of Sub-Squares using stripSum[,]
for (var i = 0; i < N - k + 1; i++)
{
// Calculate and print sum of first subsquare
// in this row
var sum = 0;
for (var j = 0; j < k; j++)
sum += stripSum[i][j];
// Update max_sum and position of result
if (sum > max_sum)
{
max_sum = sum;
pos.updatePosition(i, 0);
}
// Calculate sum of remaining squares in
// current row by removing the leftmost
// strip of previous sub-square and adding
// a new strip
for (var j = 1; j < N - k + 1; j++)
{
sum += (stripSum[i][j + k - 1] -
stripSum[i][j - 1]);
// Update max_sum and position of result
if (sum > max_sum)
{
max_sum = sum;
pos.updatePosition(i, j);
}
}
}
// Print the result matrix
for (var i = 0; i < k; i++)
{
for (var j = 0; j < k; j++)
{
document.write(mat[i + pos.getXPosition()][
j + pos.getYPosition()] + " ");
}
document.write("<br>");
}
}
// Driver Code
N = 5;
var mat = [[ 1, 1, 1, 1, 1 ],
[ 2, 2, 2, 2, 2 ],
[ 3, 8, 6, 7, 3 ],
[ 4, 4, 4, 4, 4 ],
[ 5, 5, 5, 5, 5 ]];
var k = 3;
document.write("Maximum sum 3 x 3 matrix is<br>");
printMaxSumSub(mat, k);
</script>
Maximum sum 3 x 3 matrix is 8 6 7 4 4 4 5 5 5
Complejidad temporal: O(N 2 ).
Espacio Auxiliar: O(N 2 ).
Artículos relacionados:
Dada una array cuadrada de nxn, encuentre la suma de todos los subcuadrados de tamaño kxk
Rectángulo de suma máxima en una array 2D
Este artículo es una contribución de Aarti_Rathi y Aditya Goel . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA