Considere un tablero de ajedrez NXN con obstáculos Queen y K. La Reina no puede atravesar obstáculos. Dada la posición (x, y) de la reina, la tarea es encontrar el número de celdas que la reina puede mover.
Ejemplos:
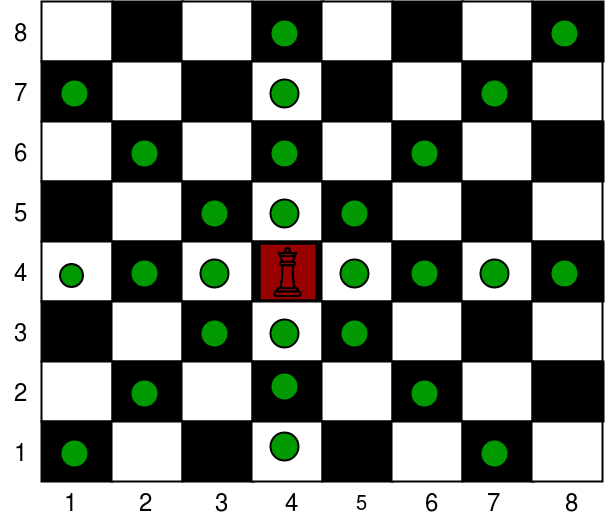
Input : N = 8, x = 4, y = 4,
K = 0
Output : 27
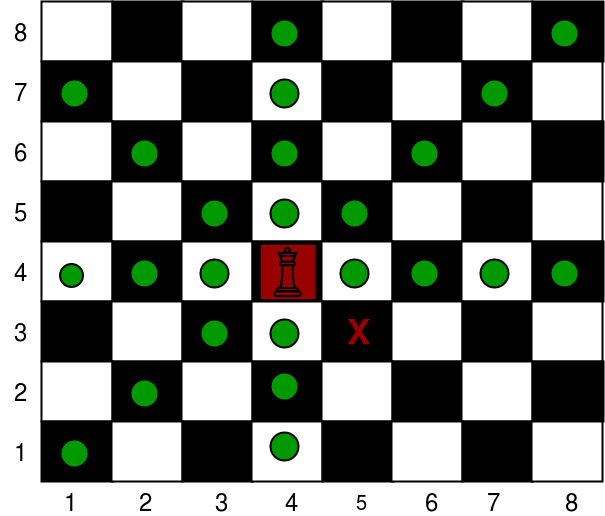
Input : N = 8, x = 4, y = 4,
K = 1, kx1 = 3, ky1 = 5
Output : 24
Método 1:
La idea es iterar sobre las celdas que la reina puede atacar y detenerse hasta que haya un obstáculo o final del tablero. Para hacer eso, necesitamos iterar horizontal, vertical y diagonalmente. Los movimientos desde la posición (x, y) pueden ser:
(x+1, y): one step horizontal move to the right. (x-1, y): one step horizontal move to the left. (x+1, y+1): one step diagonal move up-right. (x-1, y-1): one step diagonal move down-left. (x-1, y+1): one step diagonal move left-up. (x+1, y-1): one step diagonal move right-down. (x, y+1): one step downward. (x, y-1): one step upward.
A continuación se muestra la implementación en C++ de este enfoque:
C++
// C++ program to find number of cells a queen can move
// with obstacles on the chessboard
#include<bits/stdc++.h>
using namespace std;
// Return if position is valid on chessboard
int range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
int check(int n, int x, int y, int xx, int yy,
map <pair<int, int>, int> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp[{x, y}])
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
int numberofPosition(int n, int k, int x, int y,
int obstPosx[], int obstPosy[])
{
int x1, y1, ans = 0;
map <pair<int, int>, int> mp;
// Mapping each obstacle's position
while(k--)
{
x1 = obstPosx[k];
y1 = obstPosy[k];
mp[{x1, y1}] = 1;
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
ans += check(n, x-1, y-1, -1, -1, mp);
return ans;
}
// Driven Program
int main()
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int obstPosx[] = { 3 }; // x position of obstacles
int obstPosy[] = { 5 }; // y position of obstacles
cout << numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) << endl;
return 0;
}
Java
// Java program to find number of cells a queen can move
// with obstacles on the chessboard
import java.util.*;
class GFG{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
static boolean range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
static int check(int n, int x, int y, int xx, int yy,
HashMap <pair, Integer> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp.containsKey(new pair(x, y)))
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
static int numberofPosition(int n, int k, int x, int y,
int obstPosx[], int obstPosy[])
{
int x1, y1, ans = 0;
HashMap <pair, Integer> mp = new HashMap<>();
// Mapping each obstacle's position
while(k>0)
{
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.put(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
public static void main(String[] args)
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int obstPosx[] = { 3 }; // x position of obstacles
int obstPosy[] = { 5 }; // y position of obstacles
System.out.print(numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) +"\n");
}
}
// This code contributed by Rajput-Ji
Python3
# Python program to find number of cells a queen can move
# with obstacles on the chessboard
class pair :
def __init__(self, first, second):
self.first = first
self.second = second
# Return if position is valid on chessboard
def range(n , x , y):
return (x <= n and x > 0 and y <= n and y > 0)
# Return the number of moves with a given direction
def check(n , x , y , xx , yy, mp):
ans = 0
# Checking valid move of Queen in a direction.
while range(n, x, y) and pair(x, y) not in mp :
x += xx
y += yy
ans = ans+1
return ans
# Return the number of position a Queen can move.
def numberofPosition(n , k , x , y , obstPosx , obstPosy):
ans = 0
mp = {}
# Mapping each obstacle's position
while (k > 0):
k -= 1
x1 = obstPosx[k]
y1 = obstPosy[k]
mp[pair(x1, y1)] = 1
# Fetching number of position a queen can
# move in each direction.
ans += check(n, x + 1, y, 1, 0, mp)
ans += check(n, x - 1, y, -1, 0, mp)
ans += check(n, x, y + 1, 0, 1, mp)
ans += check(n, x, y - 1, 0, -1, mp)
ans += check(n, x + 1, y + 1, 1, 1, mp)
ans += check(n, x + 1, y - 1, 1, -1, mp)
ans += check(n, x - 1, y + 1, -1, 1, mp)
return ans
# Driven Program
n = 8 # Chessboard size
k = 1 # Number of obstacles
Qposx = 4 # Queen x position
Qposy = 4 # Queen y position
obstPosx = [ 3 ] # x position of obstacles
obstPosy = [ 5 ] # y position of obstacles
print(numberofPosition(n, k, Qposx, Qposy, obstPosx, obstPosy))
# This code is contributed by shinjanpatra
C#
// C# program to find number of cells a queen can move
// with obstacles on the chessboard
using System;
using System.Collections.Generic;
public class GFG{
public class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
static bool range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
static int check(int n, int x, int y, int xx, int yy,
Dictionary <pair, int> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp.ContainsKey(new pair(x, y)))
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
static int numberofPosition(int n, int k, int x, int y,
int []obstPosx, int []obstPosy)
{
int x1, y1, ans = 0;
Dictionary <pair, int> mp = new Dictionary<pair, int>();
// Mapping each obstacle's position
while(k>0)
{
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.Add(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
public static void Main(String[] args)
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int []obstPosx = { 3 }; // x position of obstacles
int []obstPosy = { 5 }; // y position of obstacles
Console.Write(numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) +"\n");
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript program to find number of cells a queen can move
// with obstacles on the chessboard
class pair {
constructor(first , second) {
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
function range(n , x , y) {
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
function check(n , x , y , xx , yy, mp) {
var ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && !mp.has(new pair(x, y))) {
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
function numberofPosition(n , k , x , y , obstPosx , obstPosy) {
var x1, y1, ans = 0;
var mp = new Map();
// Mapping each obstacle's position
while (k > 0) {
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.set(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x - 1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y - 1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y - 1, 1, -1, mp);
ans += check(n, x - 1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
var n = 8; // Chessboard size
var k = 1; // Number of obstacles
var Qposx = 4; // Queen x position
var Qposy = 4; // Queen y position
var obstPosx = [ 3 ]; // x position of obstacles
var obstPosy = [ 5 ]; // y position of obstacles
document.write(numberofPosition(n, k, Qposx, Qposy, obstPosx, obstPosy) + "\n");
// This code is contributed by Rajput-Ji
</script>
24
Complejidad de Tiempo: O(n 2 )
Espacio Auxiliar: O(n)
Método 2:
La idea es iterar sobre los obstáculos y para aquellos que están en el camino de la reina, calculamos las celdas libres hasta ese obstáculo. Si no hay ningún obstáculo en el camino, tenemos que calcular el número de celdas libres hasta el final del tablero en esa dirección.
Para cualquier (x 1 , y 1 ) y (x 2 , y 2 ):
- Si están horizontalmente al mismo nivel: abs(x 1 – x 2 – 1)
- Si están verticalmente al mismo nivel: abs(y 1 – y 2 – 1) es el número de celdas libres entre ellas.
- Si son diagonales: abs(x 1 – x 2 – 1) o abs(y 1 – y 2 – 1) es el número de celdas libres entre ellas.
A continuación se muestra la implementación de este enfoque:
C++
// C++ program to find number of cells a queen can move
// with obstacles on the chessboard
#include<bits/stdc++.h>
using namespace std;
// Return if position is valid on chessboard
int range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
int check(int n, int x, int y, int xx, int yy,
map <pair<int, int>, int> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp[{x, y}])
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
int numberofPosition(int n, int k, int x, int y,
int obstPosx[], int obstPosy[])
{
int x1, y1, ans = 0;
map <pair<int, int>, int> mp;
// Mapping each obstacle's position
while(k--)
{
x1 = obstPosx[k];
y1 = obstPosy[k];
mp[{x1, y1}] = 1;
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
ans += check(n, x-1, y-1, -1, -1, mp);
return ans;
}
// Driven Program
int main()
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int obstPosx[] = { 3 }; // x position of obstacles
int obstPosy[] = { 5 }; // y position of obstacles
cout << numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) << endl;
return 0;
}
Java
// Java program to find number of cells a queen can move
// with obstacles on the chessboard
import java.util.*;
class GFG{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
static boolean range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
static int check(int n, int x, int y, int xx, int yy,
HashMap <pair, Integer> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp.containsKey(new pair(x, y)))
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
static int numberofPosition(int n, int k, int x, int y,
int obstPosx[], int obstPosy[])
{
int x1, y1, ans = 0;
HashMap <pair, Integer> mp = new HashMap<>();
// Mapping each obstacle's position
while(k>0)
{
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.put(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
public static void main(String[] args)
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int obstPosx[] = { 3 }; // x position of obstacles
int obstPosy[] = { 5 }; // y position of obstacles
System.out.print(numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) +"\n");
}
}
// This code contributed by Rajput-Ji
Python3
# Python program to find number of cells a queen can move
# with obstacles on the chessboard
class pair :
def __init__(self, first, second):
self.first = first
self.second = second
# Return if position is valid on chessboard
def range(n , x , y):
return (x <= n and x > 0 and y <= n and y > 0)
# Return the number of moves with a given direction
def check(n , x , y , xx , yy, mp):
ans = 0
# Checking valid move of Queen in a direction.
while range(n, x, y) and pair(x, y) not in mp :
x += xx
y += yy
ans = ans+1
return ans
# Return the number of position a Queen can move.
def numberofPosition(n , k , x , y , obstPosx , obstPosy):
ans = 0
mp = {}
# Mapping each obstacle's position
while (k > 0):
k -= 1
x1 = obstPosx[k]
y1 = obstPosy[k]
mp[pair(x1, y1)] = 1
# Fetching number of position a queen can
# move in each direction.
ans += check(n, x + 1, y, 1, 0, mp)
ans += check(n, x - 1, y, -1, 0, mp)
ans += check(n, x, y + 1, 0, 1, mp)
ans += check(n, x, y - 1, 0, -1, mp)
ans += check(n, x + 1, y + 1, 1, 1, mp)
ans += check(n, x + 1, y - 1, 1, -1, mp)
ans += check(n, x - 1, y + 1, -1, 1, mp)
return ans
# Driven Program
n = 8 # Chessboard size
k = 1 # Number of obstacles
Qposx = 4 # Queen x position
Qposy = 4 # Queen y position
obstPosx = [ 3 ] # x position of obstacles
obstPosy = [ 5 ] # y position of obstacles
print(numberofPosition(n, k, Qposx, Qposy, obstPosx, obstPosy))
# This code is contributed by shinjanpatra
C#
// C# program to find number of cells a queen can move
// with obstacles on the chessboard
using System;
using System.Collections.Generic;
public class GFG{
public class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
static bool range(int n, int x, int y)
{
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
static int check(int n, int x, int y, int xx, int yy,
Dictionary <pair, int> mp)
{
int ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && ! mp.ContainsKey(new pair(x, y)))
{
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
static int numberofPosition(int n, int k, int x, int y,
int []obstPosx, int []obstPosy)
{
int x1, y1, ans = 0;
Dictionary <pair, int> mp = new Dictionary<pair, int>();
// Mapping each obstacle's position
while(k>0)
{
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.Add(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x-1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y-1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y-1, 1, -1, mp);
ans += check(n, x-1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
public static void Main(String[] args)
{
int n = 8; // Chessboard size
int k = 1; // Number of obstacles
int Qposx = 4; // Queen x position
int Qposy = 4; // Queen y position
int []obstPosx = { 3 }; // x position of obstacles
int []obstPosy = { 5 }; // y position of obstacles
Console.Write(numberofPosition(n, k, Qposx, Qposy,
obstPosx, obstPosy) +"\n");
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript program to find number of cells a queen can move
// with obstacles on the chessboard
class pair {
constructor(first , second) {
this.first = first;
this.second = second;
}
}
// Return if position is valid on chessboard
function range(n , x , y) {
return (x <= n && x > 0 && y <= n && y > 0);
}
// Return the number of moves with a given direction
function check(n , x , y , xx , yy, mp) {
var ans = 0;
// Checking valid move of Queen in a direction.
while (range(n, x, y) && !mp.has(new pair(x, y))) {
x += xx;
y += yy;
ans++;
}
return ans;
}
// Return the number of position a Queen can move.
function numberofPosition(n , k , x , y , obstPosx , obstPosy) {
var x1, y1, ans = 0;
var mp = new Map();
// Mapping each obstacle's position
while (k > 0) {
k--;
x1 = obstPosx[k];
y1 = obstPosy[k];
mp.set(new pair(x1, y1), 1);
}
// Fetching number of position a queen can
// move in each direction.
ans += check(n, x + 1, y, 1, 0, mp);
ans += check(n, x - 1, y, -1, 0, mp);
ans += check(n, x, y + 1, 0, 1, mp);
ans += check(n, x, y - 1, 0, -1, mp);
ans += check(n, x + 1, y + 1, 1, 1, mp);
ans += check(n, x + 1, y - 1, 1, -1, mp);
ans += check(n, x - 1, y + 1, -1, 1, mp);
return ans;
}
// Driven Program
var n = 8; // Chessboard size
var k = 1; // Number of obstacles
var Qposx = 4; // Queen x position
var Qposy = 4; // Queen y position
var obstPosx = [ 3 ]; // x position of obstacles
var obstPosy = [ 5 ]; // y position of obstacles
document.write(numberofPosition(n, k, Qposx, Qposy, obstPosx, obstPosy) + "\n");
// This code is contributed by Rajput-Ji
</script>
24
Complejidad de Tiempo: O(n 2 )
Espacio Auxiliar: O(n)
Este artículo es una contribución de Aarti Rathi y Anuj Chauhan . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA