NetworkX es un paquete de software en lenguaje Python para la creación, manipulación y estudio de la estructura, dinámica y función de redes complejas. Se utiliza para estudiar grandes redes complejas representadas en forma de gráficos con Nodes y aristas. Usando networkx podemos cargar y almacenar redes complejas. Podemos generar muchos tipos de redes aleatorias y clásicas, analizar la estructura de la red, construir modelos de red, diseñar nuevos algoritmos de red y dibujar redes.
Instalación del paquete:
pip install networkx
Creación de Nodes
Agregue un Node a la vez:
G.add_node(1)
Agregue una lista de Nodes:
G.add_nodes_from([2,3])
Vamos a crear Nodes en el gráfico G. Después de agregar los Nodes 1, 2, 3, 4, 7, 9

Creación de bordes:
Agregar un borde a la vez:
G.add_edge(1,2) G.add_edge(3,1) G.add_edge(2,4) G.add_edge(4,1) G.add_edge(9,1)
Agregar una lista de bordes:
G.add_edges_from([(1,2),(1,3)])
Después de agregar los bordes (1,2), (3,1), (2,4), (4,1), (9,1), (1,7), (2,9)
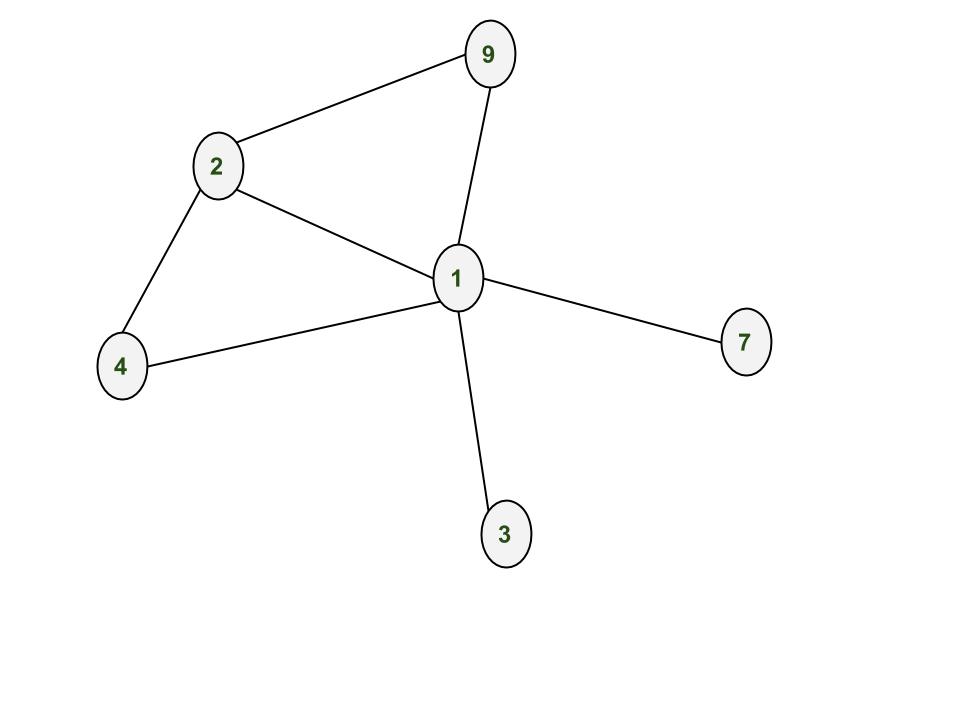
Eliminación de Nodes y bordes:
Uno puede demoler el gráfico usando cualquiera de estas funciones:
Graph.remove_node(), Graph.remove_nodes_from(), Graph.remove_edge() and Graph.remove_edges_from()
Después de eliminar el Node 3

Después de quitar el borde (1,2)

Python3
# Python program to create an undirected
# graph and add nodes and edges to a graph
# To import package
import networkx
# To create an empty undirected graph
G = networkx.Graph()
# To add a node
G.add_node(1)
G.add_node(2)
G.add_node(3)
G.add_node(4)
G.add_node(7)
G.add_node(9)
# To add an edge
# Note graph is undirected
# Hence order of nodes in edge doesn't matter
G.add_edge(1,2)
G.add_edge(3,1)
G.add_edge(2,4)
G.add_edge(4,1)
G.add_edge(9,1)
G.add_edge(1,7)
G.add_edge(2,9)
# To get all the nodes of a graph
node_list = G.nodes()
print("#1")
print(node_list)
# To get all the edges of a graph
edge_list = G.edges()
print("#2")
print(edge_list)
# To remove a node of a graph
G.remove_node(3)
node_list = G.nodes()
print("#3")
print(node_list)
# To remove an edge of a graph
G.remove_edge(1,2)
edge_list = G.edges()
print("#4")
print(edge_list)
# To find number of nodes
n = G.number_of_nodes()
print("#5")
print(n)
# To find number of edges
m = G.number_of_edges()
print("#6")
print(m)
# To find degree of a node
# d will store degree of node 2
d = G.degree(2)
print("#7")
print(d)
# To find all the neighbor of a node
neighbor_list = G.neighbors(2)
print("#8")
print(neighbor_list)
#To delete all the nodes and edges
G.clear()
Producción:
#1 [1, 2, 3, 4, 7, 9] #2 [(1, 9), (1, 2), (1, 3), (1, 4), (1, 7), (2, 4), (2, 9)] #3 [1, 2, 4, 7, 9] #4 [(1, 9), (1, 4), (1, 7), (2, 4), (2, 9)] #5 5 #6 5 #7 2 #8 [4, 9]
En la próxima publicación, discutiremos cómo crear gráficos ponderados, gráficos dirigidos, gráficos múltiples. Cómo dibujar gráficos. En publicaciones posteriores, veremos cómo usar funciones integradas como la búsqueda en profundidad, también conocida como dfs, la búsqueda en amplitud, también conocida como BFS, el algoritmo de ruta más corta de dijkstra.
Este artículo es una contribución de Pratik Chhajer . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA