El sumador produce un retraso en la propagación del acarreo mientras realiza otras operaciones aritméticas como multiplicaciones y divisiones, ya que utiliza varios pasos de sumas o restas. Este es un problema importante para el sumador y, por lo tanto, mejorar la velocidad de la suma mejorará la velocidad de todas las demás operaciones aritméticas. Por lo tanto, es de gran importancia reducir el retardo de propagación del acarreo de los sumadores. Existen diferentes enfoques de diseño lógico que se han empleado para superar el problema de propagación de acarreo. Un enfoque ampliamente utilizado es emplear una anticipación de acarreo que resuelve este problema calculando las señales de acarreo por adelantado, en función de las señales de entrada. Este tipo de circuito sumador se llama sumador anticipado de acarreo.
Aquí se generará una señal de acarreo en dos casos:
- Los bits de entrada A y B son 1
- Cuando uno de los dos bits es 1 y el carry-in es 1.
En los sumadores de acarreo de ondulación, para cada bloque de sumadores, los dos bits que se van a agregar están disponibles instantáneamente. Sin embargo, cada bloque sumador espera que llegue el acarreo de su bloque anterior. Por lo tanto, no es posible generar la suma y el acarreo de ningún bloque hasta que se conozca el acarreo de entrada. El ![]() bloque espera a que el
bloque espera a que el ![]() bloque produzca su acarreo. Por lo tanto, habrá un retraso de tiempo considerable que es un retraso de propagación de acarreo.
bloque produzca su acarreo. Por lo tanto, habrá un retraso de tiempo considerable que es un retraso de propagación de acarreo.

Considere el sumador de acarreo de ondulación de 4 bits anterior. La suma ![]() es producida por el sumador completo correspondiente tan pronto como se le aplican las señales de entrada. Pero la entrada de acarreo
es producida por el sumador completo correspondiente tan pronto como se le aplican las señales de entrada. Pero la entrada de acarreo ![]() no está disponible en su valor final de estado estacionario hasta que el acarreo
no está disponible en su valor final de estado estacionario hasta que el acarreo ![]() esté disponible en su valor de estado estacionario. Del mismo modo
esté disponible en su valor de estado estacionario. Del mismo modo ![]() depende de
depende de ![]() y
y ![]() de
de ![]() . Por lo tanto, aunque el acarreo debe propagarse a todas las etapas para que la salida
. Por lo tanto, aunque el acarreo debe propagarse a todas las etapas para que la salida ![]() y el acarreo
y el acarreo ![]() establezcan su valor final de estado estable.
establezcan su valor final de estado estable.
El tiempo de propagación es igual al retardo de propagación de cada bloque sumador, multiplicado por el número de bloques sumadores en el circuito. Por ejemplo, si cada etapa sumadora completa tiene un retraso de propagación de 20 nanosegundos, ![]() alcanzará su valor final correcto después de 60 (20 × 3) nanosegundos. La situación empeora si ampliamos el número de etapas para agregar más cantidad de bits.
alcanzará su valor final correcto después de 60 (20 × 3) nanosegundos. La situación empeora si ampliamos el número de etapas para agregar más cantidad de bits.
Sumador de anticipación de
acarreo: un sumador de anticipación de acarreo reduce el retraso de propagación mediante la introducción de hardware más complejo. En este diseño, el diseño de acarreo de ondulación se transforma adecuadamente de modo que la lógica de acarreo sobre grupos fijos de bits del sumador se reduce a una lógica de dos niveles. Vamos a discutir el diseño en detalle.
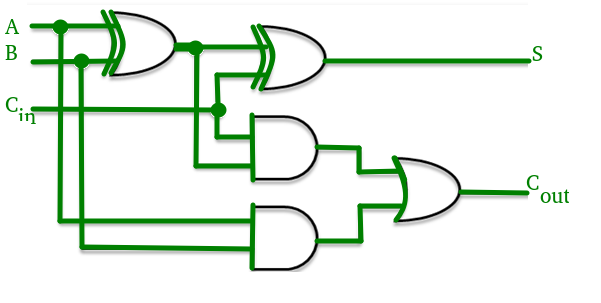

Considere el circuito sumador completo que se muestra arriba con la tabla de verdad correspondiente. Definimos dos variables como ‘carry generar’ ![]() y ‘carry propagar’
y ‘carry propagar’ ![]() entonces,
entonces, 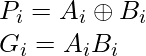
La salida de suma y la salida de acarreo se pueden expresar en términos de generación de acarreo ![]() y propagación de acarreo
y propagación de acarreo ![]() como
como
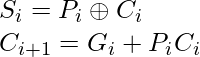
where ![]() produces the carry when both
produces the carry when both ![]() ,
, ![]() are 1 regardless of the input carry.
are 1 regardless of the input carry. ![]() is associated with the propagation of carry from
is associated with the propagation of carry from ![]() to
to ![]() .
.
La función booleana de salida de acarreo de cada etapa en un sumador anticipado de acarreo de 4 etapas se puede expresar como
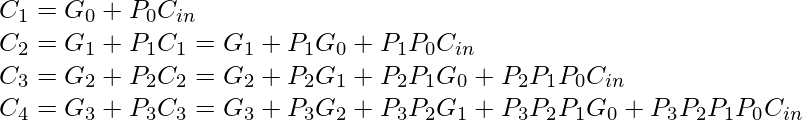
De las ecuaciones booleanas anteriores podemos observar que ![]() no tiene que esperar
no tiene que esperar ![]() y
y ![]() propagarse, sino que en realidad
propagarse, sino que en realidad ![]() se propaga al mismo tiempo que
se propaga al mismo tiempo que ![]() y
y ![]() . Dado que la expresión booleana para cada salida de acarreo es la suma de los productos, estos pueden implementarse con un nivel de compuertas AND seguido de una compuerta OR.
. Dado que la expresión booleana para cada salida de acarreo es la suma de los productos, estos pueden implementarse con un nivel de compuertas AND seguido de una compuerta OR.
La implementación de tres funciones booleanas para cada salida de acarreo ( ![]() ,
, ![]() y
y ![]() ) para un generador de acarreo anticipado que se muestra en la siguiente figura.
) para un generador de acarreo anticipado que se muestra en la siguiente figura.
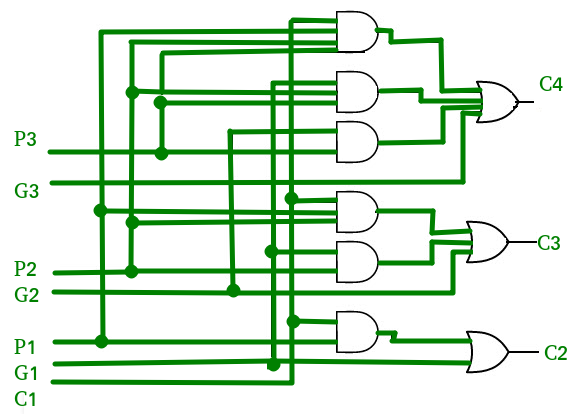
Análisis de Complejidad de Tiempo:
Podríamos pensar en un sumador anticipado de acarreo como compuesto de dos «partes»
- La parte que calcula el acarreo de cada bit.
- La parte que suma los bits de entrada y el acarreo para cada posición de bit.
La ![]() complejidad surge de la parte que genera el acarreo, no del circuito que agrega los bits.
complejidad surge de la parte que genera el acarreo, no del circuito que agrega los bits.
Ahora, para la generación del ![]() bit de acarreo, necesitamos realizar un AND entre (n+1) entradas. La complejidad del sumador se reduce a cómo realizamos esta operación AND. Si tenemos compuertas AND, cada una con un fan-in (número de entradas aceptadas) de k, entonces podemos encontrar el AND de todos los bits en el
bit de acarreo, necesitamos realizar un AND entre (n+1) entradas. La complejidad del sumador se reduce a cómo realizamos esta operación AND. Si tenemos compuertas AND, cada una con un fan-in (número de entradas aceptadas) de k, entonces podemos encontrar el AND de todos los bits en el ![]() tiempo. Esto se representa en notación asintótica como
tiempo. Esto se representa en notación asintótica como ![]() .
.
Ventajas y desventajas de Carry Look-Ahead Adder:
Ventajas –
- El retardo de propagación se reduce.
- Proporciona la lógica de adición más rápida.
Desventajas –
- El circuito sumador Carry Look-ahead se complica a medida que aumenta el número de variables.
- El circuito es más costoso ya que involucra más cantidad de hardware.
NOTA :
Para que el sumador anticipado de acarreo de n bits evalúe todos los bits de acarreo, requiere [n(n + 1)]/2 compuertas AND y n compuertas OR.
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
- GATE CS 2016 (Conjunto-1), Pregunta 43
- GATE CS 2004, Pregunta 90
- GATE CS 2007, Pregunta 85
- GATE CS 2006, Pregunta 85
- GATE CS 1997, Pregunta 15
Referencias –
iitkgp.virtual-labs
Carry-lookahead sumador – Wikipedia
Publicación traducida automáticamente
Artículo escrito por Samujjal Das y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA