Estructuras de datos y algoritmos | conjunto 5

Se han hecho las siguientes preguntas en el examen GATE CS.

1. Considere la siguiente función C.

float f(float x, int y) 
{ 
  float p, s; int i; 
  for (s=1, p=1, i=1; i < y; i ++) 
  { 
    p*= x/i; 
    s+=p; 
  } 
  return s; 
}   

Para valores grandes de y, el valor de retorno de la función f se aproxima mejor (GATE CS 2003)
a) x^y
b) e^x
c) ln(1 + x)
d) x^x

Respuesta (b)
La función f() es una implementación de la Serie de Taylor para calcular e^x

   e^x = 1 + x + x^2/2! + x^3/3! + ---

Más es el valor de y f() devolverá un valor más preciso de e^x

Referencias:
http://en.wikipedia.org/wiki/E_%28mathematical_constant%29

2. En el peor de los casos, el número de comparaciones necesarias para buscar un elemento dado en una lista enlazada de longitud n es (GATE CS 2002)
a) log 2 n
b) n/2
c) log 2 n – 1
d) norte

Respuesta(d)
En el peor de los casos, el elemento a buscar debe compararse con todos los elementos de la lista enlazada.

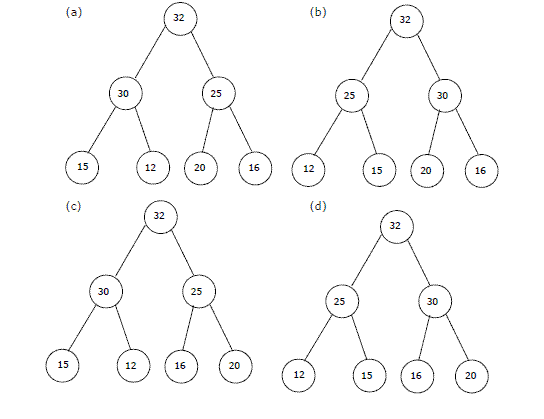
3. Los elementos 32, 15, 20, 30, 12, 25, 16 se insertan uno por uno en el orden indicado en un Max Heap. El Max Heap resultante es.

respuesta (a)

4. Considere las siguientes tres afirmaciones
I (n + k)^m = Θ(n^m), donde k y m son constantes
II 2^(n + 1) = 0(2^n)
III 2^(2n + 1) = 0(2^n)
¿Cuáles de estas afirmaciones son correctas? (GATE CS 2003)
(a) I y II
(b) I y III
(c) II y III
(d) I, II y III

Respuesta (a)

(I)  (n+m)^k = n^k + c1*n^(k-1) + ... k^m = Θ(n^k)
(II)  2^(n+1) = 2*2^n = O(2^n)

5. Se usa una única array A[1..MAXSIZE] para implementar dos pilas. Las dos pilas crecen desde los extremos opuestos de la array. Las variables top1 y top2 (topl< top 2) apuntan a la ubicación del elemento superior en cada una de las pilas. Si se va a usar el espacio de manera eficiente, la condición para «pila llena» es (GATE CS 2004)
a) (top1 = MAXSIZE/2) y (top2 = MAXSIZE/2+1)
b) top1 + top2 = MAXSIZE
c) (top1= MAXSIZE/2) o (top2 = MAXSIZE)
d) top1= top2 -1

Respuesta (d)
Si vamos a usar el espacio de manera eficiente, entonces el tamaño de cualquier pila puede ser mayor que MAXSIZE/2.
Ambas pilas crecerán desde ambos extremos y si la parte superior de la pila se acerca a la otra parte superior, las pilas estarán llenas. Por lo tanto, la condición será top1 = top2 -1 (dado que top1 < top2)

Escriba comentarios si encuentra incorrecta alguna de las respuestas/explicaciones anteriores.