Matemáticas | Graficar isomorfismos y conectividad

Isomorfismo :

Considere los siguientes dos gráficos:

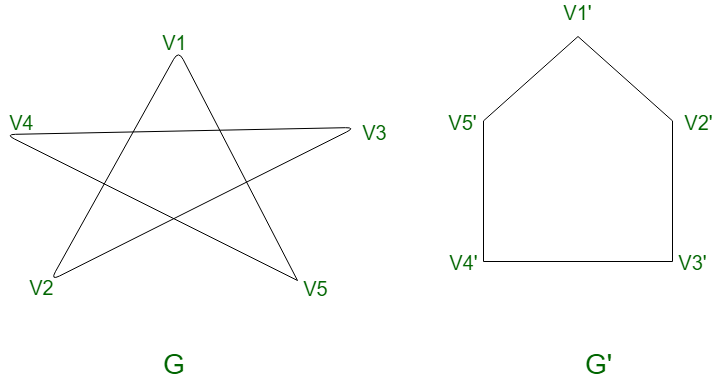
Are the graphs $G$ and $G^{\prime}$ the same?

Si tu respuesta es no, entonces debes repensarlo. La disposición gráfica de los vértices y las aristas hace que se vean diferentes, pero son el mismo gráfico. También observe que el gráfico $G^{\prime}$ es un ciclo, específicamente $C_{5}$ . Para saber más acerca de los gráficos de ciclo, lea Conceptos básicos de teoría de gráficos .

Formalmente,
“Las gráficas simples $G_{1} = (V_{1}, E_{1})$ y $G_{2} = (V_{2}, E_{2})$ son isomorfas si existe una función biyectiva $f$ de $V1$ a $V2$ con la propiedad de que $a$ y $b$ son adyacentes en $G_{1}$ si y solo si $f(a)$ y $f(b)$ son adyacentes en $G_{2}\:\forall a,b \in V_{1}$ .”

Ejemplo: Demuestre que las gráficas $G$ y $G^{\prime}$ mencionadas anteriormente son isomorfas.

Solución : Sea $f$ una función biyectiva de $V$ a $V^{\prime}$ .
Sea adyacente a y en , y es adyacente a y en De manera similar, se puede demostrar que la adyacencia se conserva para todos los vértices
$v1^{\prime} = f(v1)$
$v2^{\prime} = f(v5)$
$v3^{\prime} = f(v3)$
$v4^{\prime} = f(v4)$
$v5^{\prime} = f(v2)$
. Por lo tanto, y son isomorfos.
$v1$ $v2$ $v3$ $G$
$f(v1) = v1^{\prime}$ $f(v2) = v5$ $f(v3) = v3$ $G^{\prime}$

$G$ $G^{\prime}$

Probar que los gráficos anteriores son isomorfos fue fácil ya que los gráficos eran pequeños, pero a menudo es difícil determinar si dos gráficos simples son isomorfos. Esto se debe a que existen $n!$ funciones biyectivas posibles entre los conjuntos de vértices de dos gráficos simples con $n$ vértices. Probar la correspondencia para cada una de las funciones no es práctico para valores grandes de n.
Aunque a veces no es tan difícil saber si dos gráficos no son isomorfos. Para probar que las gráficas dadas no son isomorfas, podríamos encontrar alguna propiedad que sea característica de una gráfica y no de la otra. Si fueran isomorfos, la propiedad se mantendría, pero como no lo es, los gráficos no son isomorfos.
Tal propiedad que se conserva por isomorfismo se llamagráficamente invariante .

Algunas gráficas invariantes incluyen: el número de vértices, el número de aristas, los grados de los vértices y la duración del ciclo, etc.

Puedes decir que los gráficos dados son isomorfos si tienen:

Igual número de vértices.
Igual número de aristas.
Misma secuencia de grados
Mismo número de circuito de longitud particular

En la mayoría de los gráficos, basta con comprobar las tres primeras condiciones.

Nota importante: el complementario de un gráfico tiene los mismos vértices y tiene aristas entre dos vértices si y solo si no había arista entre ellos en el gráfico original. En consecuencia, $G$ se dice que un grafo es autocomplementario si el grafo y su complemento son isomorfos.

Conectividad:

La mayoría de los problemas que pueden resolverse mediante gráficos tratan de encontrar caminos, distancias u otra información similar óptimas. Casi todos estos problemas implican encontrar caminos entre los Nodes del gráfico.

Camino: un camino de longitud $n$ desde $u$ hasta $v$ es una secuencia de $n$ aristas $e_{1},...,e_{n}$ tales que $e_{1}$ está asociado con $\{x_{0}, x_{1}\}$ , y así sucesivamente, con $e_{n}$ asociado con $\{x_{n-1}, x_{n}\}$ , donde $x_{0} = u$ y $x_{n} = v$ .

Nota: Un camino se llama circuito si comienza y termina en el mismo vértice. También se le llama ciclo.

La conectividad de un gráfico es un aspecto importante ya que mide la resiliencia del gráfico.
«Se dice que un grafo no dirigido es conexo si hay un camino entre cada par de vértices distintos del grafo».

Componente conectado: un componente conectado de un gráfico $G$ es un subgráfico conectado $G$ que no es un subgráfico propio de otro subgráfico conectado de $G$ .

Por ejemplo, en el siguiente diagrama, el gráfico $G_{1}$ está conectado y el gráfico $G_{2}$ está desconectado. Dado que $G_{1}$ está conectado, solo hay un componente conectado.
Pero en el caso de $G_{2}$ hay tres componentes conectados.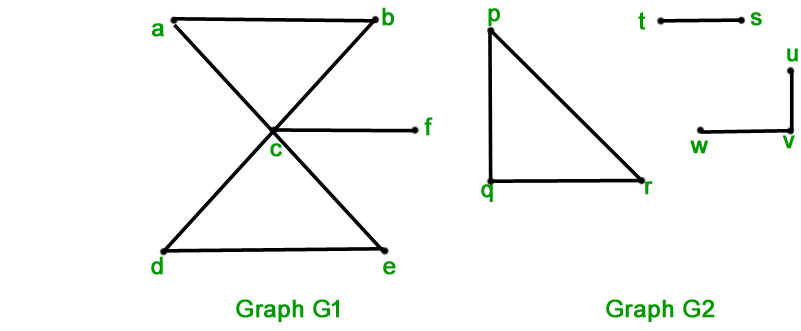

En caso de que el gráfico sea dirigido, las nociones de conectividad deben cambiarse un poco. Esto se debe a las direcciones que tienen los bordes.

Formalmente,
“Se dice que un grafo dirigido está fuertemente conectado si hay un camino desde y $a$ hacia donde y son vértices en el grafo. El gráfico está débilmente conectado si el gráfico no dirigido subyacente está conectado”. $b$ $b$ $a$ $a$ $b$

Componente fuertemente conectado:
de manera análoga a los componentes conectados en gráficos no dirigidos, un componente fuertemente conectado es un subgráfico de un gráfico dirigido que no está contenido dentro de otro componente fuertemente conectado.

Puntos de articulación –

La eliminación de un vértice y todas las aristas incidentes con él puede dar como resultado un subgrafo que tiene más componentes conexas que en los gráficos originales. Dichos vértices se denominan puntos de articulación o vértices cortados.
De manera análoga a los vértices cortados, se corta el borde , cuya eliminación da como resultado un subgrafo con más componentes conectados. Un borde cortado también se llama puente.

Conjunto de cortes: en un gráfico conectado $G$ , un conjunto de cortes es un conjunto de aristas que, cuando se quitan de las $G$ hojas $G$ , se desconectan, siempre que no haya un subconjunto adecuado de estas aristas que se desconecte $G$ .

Caminos e Isomorfismos –

A veces, aunque dos gráficos no son isomorfos, sus gráficos son invariantes: el número de vértices, el número de aristas y los grados de los vértices coinciden. En este caso, las rutas y los circuitos pueden ayudar a diferenciar entre los gráficos.

Ejemplo: ¿los dos gráficos que se muestran a continuación son isomorfos?
Solución: ambos gráficos tienen 6 vértices, 9 aristas y la secuencia de grados es la misma. Sin embargo, el segundo gráfico tiene un circuito de longitud 3 y la longitud mínima de cualquier circuito en el primer gráfico es 4. Por lo tanto, los gráficos dados no son isomorfos.

Preguntas de GATE CS Corner

Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.

1. GATE CS 2013, Pregunta 24
2. GATE CS 2012, Pregunta 26
3. GATE CS 2012, Pregunta 38
4. GATE CS 2014 Conjunto-1, Pregunta 13
5. GATE CS 2014 Conjunto-2, Pregunta 61
6. GATE CS 2015 Serie 2, Pregunta 38
7. GATE CS 2015 Serie 2, Pregunta 60

Referencias-

Isomorfismo de grafos –
Conectividad de grafos de Wikipedia –
Matemáticas discretas de Wikipedia y sus aplicaciones, por Kenneth H Rosen

Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta