Prerrequisito: diseñar autómatas finitos
. Problema: construir una máquina DFA sobre el alfabeto de entrada ![]() = {0, 1}, que acepte:
= {0, 1}, que acepte:
- Número impar de 0 o número par de 1
- Número impar de 0 y número par de 1
- Ya sea un número impar de 0 o un número par de 1, pero no los dos juntos
Solución: primero diseñe dos máquinas separadas para las dos condiciones:
- Aceptando solo un número impar de 0
- Aceptar solo un número par de 1
Luego, combine estos dos y encuentre los estados finales requeridos.


Para fusionar estas dos máquinas, tomaremos el producto cartesiano de los estados de estas dos máquinas:

El estado inicial de estos DFA será el estado que contiene los estados iniciales de esas dos máquinas separadas. Como q0 y q2 son los estados iniciales, q0q2 es el estado inicial del DFA final.
Ahora comience a diseñar todos los DFA uno por uno:
- Número impar de 0 o número par de 1:
Esta máquina acepta los idiomas que contienen números impares. de 0 o incluso no. de 1s. Como sabemos q1 indica impar no. de 0 y q2 indica par no. de 1s. Entonces, los estados finales del DFA requerido contendrán q1 o q2.
.’. Estados finales = {(q0q2), (q1q2), (q1q3)}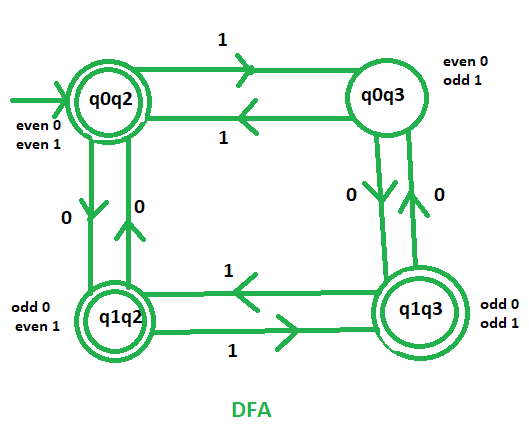
Este es nuestro DFA requerido que acepta los idiomas que contienen números impares. de 0 o incluso no. de 1s.
- Número impar de 0 y número par de 1:
Esta máquina acepta los idiomas que contienen números impares. de 0 e incluso no. de 1s. Como sabemos q1 indica impar no. de 0 y q2 indica par no. de 1s. Entonces, los estados finales del DFA requerido contendrán tanto q1 como q2.
.’. Estado final = {(q1q2)}
Este es nuestro DFA requerido que acepta los idiomas que contienen números impares. y 0 o incluso no. de 1s.
- Ya sea un número impar de 0 o un número par de 1, pero no los dos juntos:
Esta máquina acepta los idiomas que contienen números impares. de 0 o incluso no. de 1, pero no los idiomas que contienen ambos números impares. de 0 e incluso no. de 1s. Como sabemos q1 indica impar no. de 0 y q2 indica par no. de 1s. Entonces, los estados finales del DFA requerido contendrán exactamente uno entre q1 y q2.
.’. Estados finales = {(q0q2), (q1q3)}
Este es nuestro DFA requerido que acepta los idiomas que contienen números impares. de 0 o incluso no. de 1 pero no los dos juntos.
Publicación traducida automáticamente
Artículo escrito por SUDIPTADANDAPAT y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA