Si un sistema no emplea un algoritmo de prevención de interbloqueo o de evitación de interbloqueo, entonces puede ocurrir una situación de interbloqueo. En este caso-
- Aplique un algoritmo para examinar el estado del sistema y determinar si se ha producido un interbloqueo o no.
- Aplicar un algoritmo para recuperarse del punto muerto. Para obtener más información, consulte Recuperación de interbloqueo
Algoritmo de evitación de interbloqueo/algoritmo de banqueros :
el algoritmo emplea estructuras de datos que varían varias veces:
- Disponible:
un vector de longitud m indica la cantidad de recursos disponibles de cada tipo. - Asignación:
una array n*m define la cantidad de recursos de cada tipo actualmente asignados a un proceso. La columna representa el recurso y las filas representan el proceso. - Solicitud:
una array n*m indica la solicitud actual de cada proceso. Si request[i][j] es igual a k, entonces el proceso Pi está solicitando k más instancias del tipo de recurso R j .
Este algoritmo ya ha sido discutido aquí .
Ahora, el algoritmo Bankers incluye un algoritmo de seguridad/algoritmo de detección
de punto muerto. El algoritmo para averiguar si un sistema está en un estado seguro se puede describir de la siguiente manera:
Pasos del algoritmo:
- Sean Work y Finish vectores de longitud m y n respectivamente. Inicializar Trabajo = Disponible . Para i=0, 1, …., n-1 , si Request i = 0, entonces Finish[i] = true; de lo contrario, Finalizar[i] = falso.
- Encuentre un índice i tal que ambos
a) Terminar[i] == falso
b) Solicitar i <= Trabajar
Si no existe tal i , vaya al paso 4. - Trabajo = Trabajo + Asignación i
Terminar [i] = verdadero
Vaya al Paso 2. - Si Finish[i]== false para alguna i, 0<=i<n, entonces el sistema está en un estado de interbloqueo. Además, si Finish[i]==false , el proceso P i está bloqueado.
Por ejemplo,
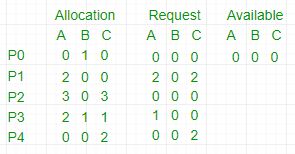
- En esto, Trabajo = [0, 0, 0] &
Terminar = [falso, falso, falso, falso, falso]
- i=0 se selecciona como Finalizar[0] = falso y [0, 0, 0]<=[0, 0, 0].
- Trabajar =[0, 0, 0]+[0, 1, 0] =>[0, 1, 0] &
Finalizar = [verdadero, falso, falso, falso, falso].
- i=2 se selecciona como Finalizar[2] = falso y [0, 0, 0]<=[0, 1, 0].
- Trabajar =[0, 1, 0]+[3, 0, 3] =>[3, 1, 3] &
Finalizar = [verdadero, falso, verdadero, falso, falso].
- i=1 se selecciona como Finalizar[1] = falso y [2, 0, 2]<=[3, 1, 3].
- Trabajar =[3, 1, 3]+[2, 0, 0] =>[5, 1, 3] &
Finalizar = [verdadero, verdadero, verdadero, falso, falso].
- i=3 se selecciona como Finalizar[3] = falso y [1, 0, 0]<=[5, 1, 3].
- Trabajar =[5, 1, 3]+[2, 1, 1] =>[7, 2, 4] &
Finalizar = [verdadero, verdadero, verdadero, verdadero, falso].
- i=4 se selecciona como Finalizar[4] = falso y [0, 0, 2]<=[7, 2, 4].
- Trabajar =[7, 2, 4]+[0, 0, 2] =>[7, 2, 6] &
Finalizar = [verdadero, verdadero, verdadero, verdadero, verdadero].
- Dado que Finalizar es un vector de todo verdadero, significa que no hay punto muerto en este ejemplo.