Todos los tipos topológicos de un gráfico acíclico dirigido

La ordenación topológica para un gráfico cíclico dirigido ( DAG ) es una ordenación lineal de vértices tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. La clasificación topológica de un gráfico no es posible si el gráfico no es un DAG.

Dado un DAG, imprima todos los tipos topológicos del gráfico.

For example, consider the below graph.

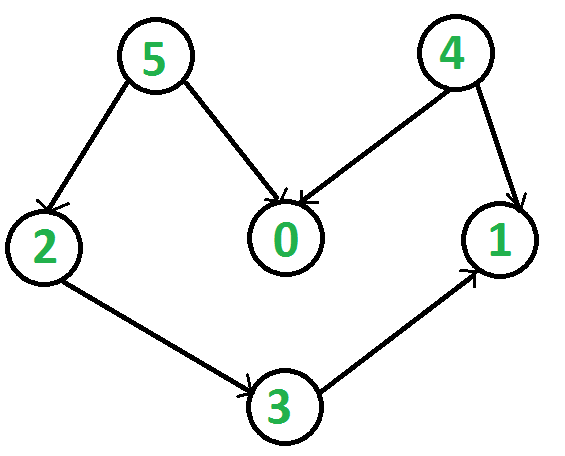
All topological sorts of the given graph are:
4 5 0 2 3 1 
4 5 2 0 3 1 
4 5 2 3 0 1 
4 5 2 3 1 0 
5 2 3 4 0 1 
5 2 3 4 1 0 
5 2 4 0 3 1 
5 2 4 3 0 1 
5 2 4 3 1 0 
5 4 0 2 3 1 
5 4 2 0 3 1 
5 4 2 3 0 1 
5 4 2 3 1 0 

En un gráfico acíclico dirigido, muchas veces podemos tener vértices que no están relacionados entre sí, por lo que podemos ordenarlos de muchas maneras. Esta clasificación topológica diversa es importante en muchos casos, por ejemplo, si también hay algún peso relativo disponible entre los vértices, que es minimizar, entonces debemos cuidar el orden relativo y su peso relativo, lo que crea la necesidad de verificar todos los posibles ordenamientos topológicos. 

Podemos pasar por todos los pedidos posibles a través de backtracking, el paso del algoritmo es el siguiente: 

1. Inicialice todos los vértices como no visitados.
2. Ahora elija el vértice que no está visitado y tiene un grado de entrada cero y disminuya el grado de todos esos vértices en 1 (correspondiente a la eliminación de bordes) ahora agregue este vértice al resultado y llame a la función recursiva nuevamente y retroceda.
3. Después de regresar de la función, restablezca los valores de visitado, resultado y grado de entrada para la enumeración de otras posibilidades.

A continuación se muestra la implementación de los pasos anteriores.

// C++ program to print all topological sorts of a graph
#include <bits/stdc++.h>
using namespace std;
 
class Graph
{
    int V;    // No. of vertices
 
    // Pointer to an array containing adjacency list
    list<int> *adj;
 
    // Vector to store indegree of vertices
    vector<int> indegree;
 
    // A function used by alltopologicalSort
    void alltopologicalSortUtil(vector<int>& res,
                                bool visited[]);
 
public:
    Graph(int V);   // Constructor
 
    // function to add an edge to graph
    void addEdge(int v, int w);
 
    // Prints all Topological Sorts
    void alltopologicalSort();
};
 
//  Constructor of graph
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
 
    // Initialising all indegree with 0
    for (int i = 0; i < V; i++)
        indegree.push_back(0);
}
 
//  Utility function to add edge
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v's list.
 
    // increasing inner degree of w by 1
    indegree[w]++;
}
 
//  Main recursive function to print all possible
//  topological sorts
void Graph::alltopologicalSortUtil(vector<int>& res,
                                   bool visited[])
{
    // To indicate whether all topological are found
    // or not
    bool flag = false;
 
    for (int i = 0; i < V; i++)
    {
        //  If indegree is 0 and not yet visited then
        //  only choose that vertex
        if (indegree[i] == 0 && !visited[i])
        {
            //  reducing indegree of adjacent vertices
            list<int>:: iterator j;
            for (j = adj[i].begin(); j != adj[i].end(); j++)
                indegree[*j]--;
 
            //  including in result
            res.push_back(i);
            visited[i] = true;
            alltopologicalSortUtil(res, visited);
 
            // resetting visited, res and indegree for
            // backtracking
            visited[i] = false;
            res.erase(res.end() - 1);
            for (j = adj[i].begin(); j != adj[i].end(); j++)
                indegree[*j]++;
 
            flag = true;
        }
    }
 
    //  We reach here if all vertices are visited.
    //  So we print the solution here
    if (!flag)
    {
        for (int i = 0; i < res.size(); i++)
            cout << res[i] << " ";
        cout << endl;
    }
}
 
//  The function does all Topological Sort.
//  It uses recursive alltopologicalSortUtil()
void Graph::alltopologicalSort()
{
    // Mark all the vertices as not visited
    bool *visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;
 
    vector<int> res;
    alltopologicalSortUtil(res, visited);
}
 
// Driver program to test above functions
int main()
{
    // Create a graph given in the above diagram
    Graph g(6);
    g.addEdge(5, 2);
    g.addEdge(5, 0);
    g.addEdge(4, 0);
    g.addEdge(4, 1);
    g.addEdge(2, 3);
    g.addEdge(3, 1);
 
    cout << "All Topological sorts\n";
 
    g.alltopologicalSort();
 
    return 0;
}

//Java program to print all topological sorts of a graph
import java.util.*;
 
class Graph {
    int V; // No. of vertices
 
    List<Integer> adjListArray[];
 
    public Graph(int V) {
 
        this.V = V;
 
        @SuppressWarnings("unchecked")
        List<Integer> adjListArray[] = new LinkedList[V];
 
        this.adjListArray = adjListArray;
 
        for (int i = 0; i < V; i++) {
            adjListArray[i] = new LinkedList<>();
        }
    }
    // Utility function to add edge
    public void addEdge(int src, int dest) {
 
        this.adjListArray[src].add(dest);
 
    }
     
    // Main recursive function to print all possible
    // topological sorts
    private void allTopologicalSortsUtil(boolean[] visited,
                        int[] indegree, ArrayList<Integer> stack) {
        // To indicate whether all topological are found
        // or not
        boolean flag = false;
 
        for (int i = 0; i < this.V; i++) {
            // If indegree is 0 and not yet visited then
            // only choose that vertex
            if (!visited[i] && indegree[i] == 0) {
                 
                // including in result
                visited[i] = true;
                stack.add(i);
                for (int adjacent : this.adjListArray[i]) {
                    indegree[adjacent]--;
                }
                allTopologicalSortsUtil(visited, indegree, stack);
                 
                // resetting visited, res and indegree for
                // backtracking
                visited[i] = false;
                stack.remove(stack.size() - 1);
                for (int adjacent : this.adjListArray[i]) {
                    indegree[adjacent]++;
                }
 
                flag = true;
            }
        }
        // We reach here if all vertices are visited.
        // So we print the solution here
        if (!flag) {
            stack.forEach(i -> System.out.print(i + " "));
            System.out.println();
        }
 
    }
     
    // The function does all Topological Sort.
    // It uses recursive alltopologicalSortUtil()
    public void allTopologicalSorts() {
        // Mark all the vertices as not visited
        boolean[] visited = new boolean[this.V];
 
        int[] indegree = new int[this.V];
 
        for (int i = 0; i < this.V; i++) {
 
            for (int var : this.adjListArray[i]) {
                indegree[var]++;
            }
        }
 
        ArrayList<Integer> stack = new ArrayList<>();
 
        allTopologicalSortsUtil(visited, indegree, stack);
    }
     
    // Driver code
    public static void main(String[] args) {
 
        // Create a graph given in the above diagram
        Graph graph = new Graph(6);
        graph.addEdge(5, 2);
        graph.addEdge(5, 0);
        graph.addEdge(4, 0);
        graph.addEdge(4, 1);
        graph.addEdge(2, 3);
        graph.addEdge(3, 1);
 
        System.out.println("All Topological sorts");
        graph.allTopologicalSorts();
    }
}

# class to represent a graph object
class Graph:
 
    # Constructor
    def __init__(self, edges, N):
 
        # A List of Lists to represent an adjacency list
        self.adjList = [[] for _ in range(N)]
 
        # stores in-degree of a vertex
        # initialize in-degree of each vertex by 0
        self.indegree = [0] * N
 
        # add edges to the undirected graph
        for (src, dest) in edges:
 
            # add an edge from source to destination
            self.adjList[src].append(dest)
 
            # increment in-degree of destination vertex by 1
            self.indegree[dest] = self.indegree[dest] + 1
 
 
# Recursive function to find
# all topological orderings of a given DAG
def findAllTopologicalOrders(graph, path, discovered, N):
 
    # do for every vertex
    for v in range(N):
 
        # proceed only if in-degree of current node is 0 and
        # current node is not processed yet
        if graph.indegree[v] == 0 and not discovered[v]:
 
            # for every adjacent vertex u of v,
            # reduce in-degree of u by 1
            for u in graph.adjList[v]:
                graph.indegree[u] = graph.indegree[u] - 1
 
            # include current node in the path
            # and mark it as discovered
            path.append(v)
            discovered[v] = True
 
            # recur
            findAllTopologicalOrders(graph, path, discovered, N)
 
            # backtrack: reset in-degree
            # information for the current node
            for u in graph.adjList[v]:
                graph.indegree[u] = graph.indegree[u] + 1
 
            # backtrack: remove current node from the path and
            # mark it as undiscovered
            path.pop()
            discovered[v] = False
 
    # print the topological order if
    # all vertices are included in the path
    if len(path) == N:
        print(path)
 
 
# Print all topological orderings of a given DAG
def printAllTopologicalOrders(graph):
 
    # get number of nodes in the graph
    N = len(graph.adjList)
 
    # create an auxiliary space to keep track of whether vertex is discovered
    discovered = [False] * N
 
    # list to store the topological order
    path = []
 
    # find all topological ordering and print them
    findAllTopologicalOrders(graph, path, discovered, N)
 
# Driver code
if __name__ == '__main__':
 
    # List of graph edges as per above diagram
    edges = [(5, 2), (5, 0), (4, 0), (4, 1), (2, 3), (3, 1)]
 
    print("All Topological sorts")
 
    # Number of nodes in the graph
    N = 6
 
    # create a graph from edges
    graph = Graph(edges, N)
 
    # print all topological ordering of the graph
    printAllTopologicalOrders(graph)
 
# This code is contributed by Priyadarshini Kumari

All Topological sorts
4 5 0 2 3 1 
4 5 2 0 3 1 
4 5 2 3 0 1 
4 5 2 3 1 0 
5 2 3 4 0 1 
5 2 3 4 1 0 
5 2 4 0 3 1 
5 2 4 3 0 1 
5 2 4 3 1 0 
5 4 0 2 3 1 
5 4 2 0 3 1 
5 4 2 3 0 1 
5 4 2 3 1 0 

Este artículo es una contribución de Utkarsh Trivedi. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.