Medición 2D

La medición 2D se ocupa principalmente de problemas de perímetro y área. La forma es bidimensional, como triángulo, cuadrado, rectángulo, círculo, paralelogramo, etc. Este tema no tiene muchas variaciones y la mayoría de las preguntas se basan en ciertas fórmulas fijas. 

• Perímetro: La longitud del límite de una figura 2D se llama perímetro.
• Área: La región encerrada por la figura 2D se llama área.
• Teorema de Pitágoras: En un triángulo rectángulo, (Hipotenusa) ² = (Base) ² + (Altura) ²

Triángulo

Sean los tres lados del triángulo a, b y c.  

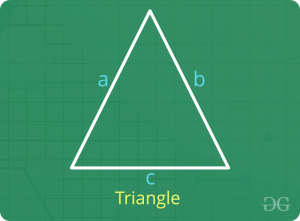
• perímetro = a + b + c
• Área 
  1. 2s = a + b + c 
     Área =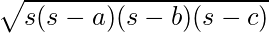 
  2. Área = 0.5 x Base x Altura Perpendicular 

Rectángulo 

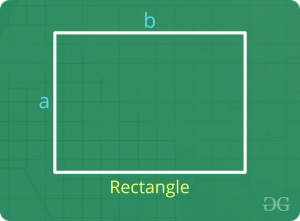
• Perímetro = 2 x (largo + ancho)
• Área = Largo x Ancho

Cuadrado

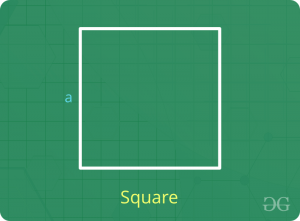
• Perímetro = 4 x Longitud lateral
• Área = (Longitud lateral) ² = 0,5 x (Longitud diagonal) ²

Paralelogramo

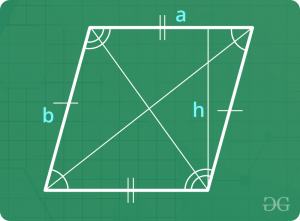
• Perímetro = 2 x Suma de lados adyacentes
• Área = Base x Altura Perpendicular 

Rombo 

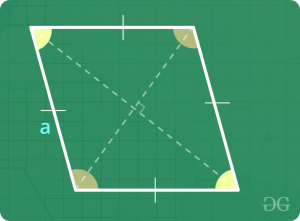
• Perímetro = 4 x Longitud lateral
• Área = 0.5 x Producto de diagonales

Trapecio

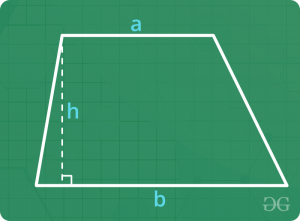
• perímetro = suma de todos los lados
• Área = 0.5 x Suma de lados paralelos x Altura perpendicular

Circulo

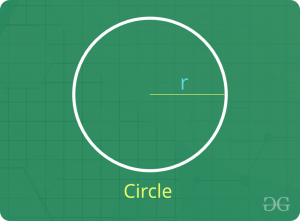
• Perímetro = 2 π Radio
• Área = π (Radio) ²
• Longitud de un arco que subtiende un ángulo θ en el centro del círculo = (π x Radio x θ) / 180
• Área de un sector que subtiende un ángulo θ en el centro del círculo = (π x Radio ² x θ) / 360

Problemas de muestra

Pregunta 1: Encuentra el perímetro y el área de un triángulo isósceles cuyos lados iguales miden 5 cm y la altura es de 4 cm. 
Solución: Aplicando el teorema de Pitágoras, 
(Hipotenusa) ² = (Base) ² + (Altura) ² 
=> (5) ² = (0.5 x Base del triángulo isósceles) ² + (4) ² 
=> 0.5 x Base del triángulo isósceles = 3 
=> Base del triángulo isósceles = 6 cm 
Por lo tanto, perímetro = suma de todos los lados = 5 + 5 + 6 = 16 cm 
Área del triángulo = 0,5 x Base x Altura = 0,5 x 6 x 4 = 12 cm ²  
  
Pregunta 2:Se utiliza una pieza rectangular de 22 cm x 7 cm de dimensión para hacer un círculo del mayor radio posible. Encuentre el área del círculo así formado. 
Solución: En preguntas como esta, el diámetro del círculo es menor que el largo y el ancho. 
Aquí, ancho Diámetro del círculo = 7 cm 
=> Radio del círculo = 3,5 cm 
Por lo tanto, área del círculo = π (Radio) ² = π (3,5) ² = 38,50 cm ²  
  
Pregunta 3: Se va a dividir una pizza en 8 piezas idénticas. ¿Cuál sería el ángulo subtendido por cada pieza en el centro del círculo? 
Solución: Por piezas idénticas, queremos decir que el área de cada pieza es la misma. 
=> Área de cada pieza = (π x Radio ²x θ) / 360 = (1/8) x Área de pizza circular 
=> (π x Radio ² x θ) / 360 = (1/8) x (π x Radio ² ) 
=> θ / 360 = 1 / 8 
=> θ = 360 / 8 = 45 
Por lo tanto, ángulo subtendido por cada pieza en el centro del círculo = 45 grados 
  
Pregunta 4: Cuatro vacas están atadas a cada esquina de un campo cuadrado de 7 cm de lado. Las vacas se atan con una cuerda de manera que cada vaca pasta el máximo campo posible y todas las vacas pastan en áreas iguales. Encuentre el área del campo sin pastorear. 
Solución: Para un pastoreo máximo e igualitario, la longitud de cada cuerda debe ser de 3,5 cm. 
=> Área pastada por 1 vaca = (π x Radio ² x θ) / 360 
=> Área pastada por 1 vaca = (π x 3.5 ²x 90) / 360 = (π x 3,5 ² ) / 4 
=> Superficie pastada por 4 vacas = 4 x [(π x 3,5 ² ) / 4] = π x 3,5 ² 
=> Superficie pastada por 4 vacas = 38,5 cm ² 
Ahora, el área del campo cuadrado = Lado ² = 7 ² = 49 cm ² 
=> Área no pastoreada = Área de campo – Área pastoreada por 4 vacas 
=> Área no pastoreada = 49 – 38,5 = 10,5 cm ²  
  
Pregunta 5: Encuentre el área de mayor cuadrado que se puede inscribir en una circunferencia de radio ‘r’. 
Solución: El cuadrado más grande que se puede inscribir en el círculo tendrá el diámetro del círculo como la diagonal del cuadrado. 
=> Diagonal del cuadrado = 2 r 
=> Lado del cuadrado = 2 r / 2 ^1/2 
=> Lado del cuadrado = 2 ^1/2 r 
Por lo tanto, área del cuadrado = Lado ² = [2 ^1/2 r] ² = 2 r ²  
  
Pregunta 6 : Un contratista emprende el trabajo de cercar un campo rectangular de 100 m de largo y 50 m de ancho. El costo de la cerca es de Rs. 2 por metro y los cargos por mano de obra son Re. 1 por metro, ambos pagados directamente al contratista. Encuentre el costo total del cercado si el 10 % del monto pagado al contratista se paga como impuesto a la autoridad de tierras. 
Solución: Costo total de cercado por metro = Rs. 2 + 1 = $. 3 
Longitud de cerca requerida = Perímetro del campo rectangular = 2 (Largo + Ancho) 
=> Longitud del cercado requerido = 2 x (100 + 50) = 300 metros 
=> Monto pagado al contratista = Rs. 3 x 300 = 900 
=> Cantidad pagada a la autoridad de tierras = 10 % de Rs. 900 = rupias 90 
por lo tanto, costo total de cercado = Rs. 900 + 90 = rupias. 990 

Problemas de Medición 2D | conjunto 2

Programas en Triangle: 

• encontrar el area de un triangulo
• Hallar el perímetro de un triángulo
• Hallar el area de un triangulo si se dan dos vectores de dos lados adyacentes
• Calcular el área y el perímetro de un triángulo equilátero
• Altura mínima de un triángulo con base y área dadas

Programas en Rectángulo: 

• programa para area y perimetro de rectangulo
• Área total de dos rectángulos superpuestos
• Área máxima de rectángulo posible con perímetro dado
• Rectángulo de área máxima seleccionando cuatro lados de la array
• Encuentre el área mínima del rectángulo con un conjunto dado de coordenadas

Programas en Square: 

• Programa para hallar el area de un cuadrado
• Área de un cuadrado a partir de la longitud de la diagonal
• Suma del área de todos los cuadrados posibles dentro de un rectángulo
• Encuentra perímetro / circunferencia de cuadrado y rectángulo

Programas en paralelogramo: 

• Programa para la Circunferencia de un Paralelogramo
• Programa para hallar el area de un paralelogramo
• Encuentra el área del paralelogramo si se dan los vectores de dos lados adyacentes

Programas sobre Rombo y Trapecio: 

• Programa para calcular area y perimetro de un rombo cuyas diagonales estan dadas
• Área del rombo más grande posible que se puede inscribir en un rectángulo
• Programa para calcular area y perimetro de trapecio

Programas en Circle: 

• Programa para hallar el area de un circulo
• Programa para hallar la Circunferencia de un Circulo
• Programa para calcular el area de un Circulo inscrito en un Cuadrado
• Area del circulo inscrito dentro del rombo
• Área de un círculo circunscrito de un cuadrado
• Área de un círculo inscrito en un hexágono regular
• Programa para hallar el Radio de la circunferencia inscrita del triangulo

Este artículo ha sido contribuido por Nishant Arora 
Por favor, escriba comentarios si tiene alguna duda relacionada con el tema discutido anteriormente, o si tiene dificultades con alguna pregunta o si le gustaría discutir una pregunta diferente a las mencionadas anteriormente. 
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.