Treap (un árbol de búsqueda binario aleatorio)

Al igual que los árboles rojo-negro y AVL , Treap es un árbol de búsqueda binario equilibrado, pero no se garantiza que tenga una altura como O (Log n). La idea es utilizar la propiedad Randomization y Binary Heap para mantener el equilibrio con alta probabilidad. La complejidad de tiempo esperada de búsqueda, inserción y eliminación es O (Inicio de sesión n).

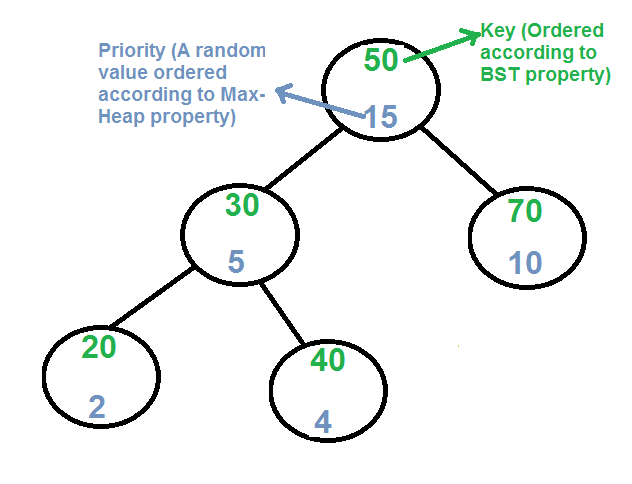
Cada Node de Treap mantiene dos valores.
1) Clave Sigue el orden BST estándar (la izquierda es más pequeña y la derecha es más grande)
2) Prioridad Valor asignado aleatoriamente que sigue la propiedad Max-Heap.

Operación básica en Treap: al
igual que otros árboles de búsqueda binarios autoequilibrados, Treap usa rotaciones para mantener la propiedad Max-Heap durante la inserción y eliminación.

T1, T2 and T3 are subtrees of the tree rooted with y (on left side) 
or x (on right side)           
                y                               x
               / \     Right Rotation          /  \
              x   T3   – – – – – – – >        T1   y 
             / \       < - - - - - - -            / \
            T1  T2     Left Rotation            T2  T3
Keys in both of the above trees follow the following order 
      keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere. 

search(x)
Realice una búsqueda BST estándar para encontrar x.

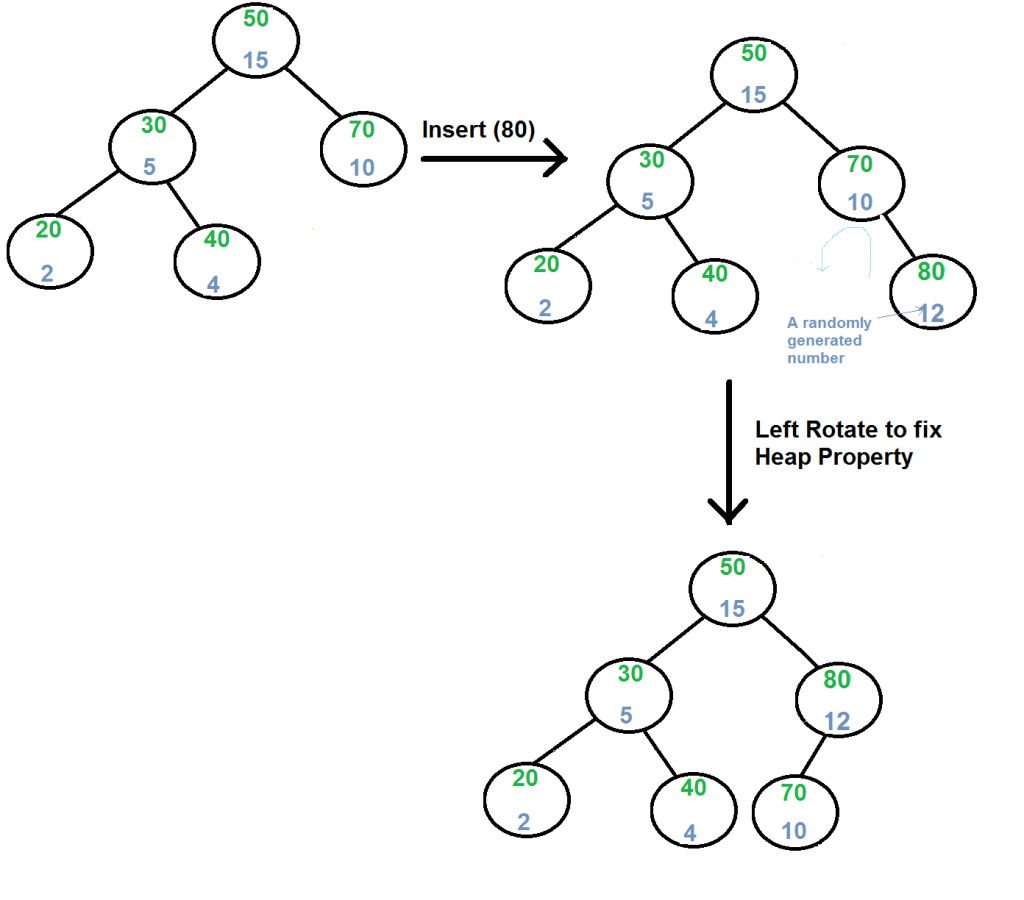
Insertar (x):
1) Crear un nuevo Node con clave igual ax y valor igual a un valor aleatorio.
2) Realice una inserción BST estándar .
3) Use rotaciones para asegurarse de que la prioridad del Node insertado siga la propiedad de montón máximo.

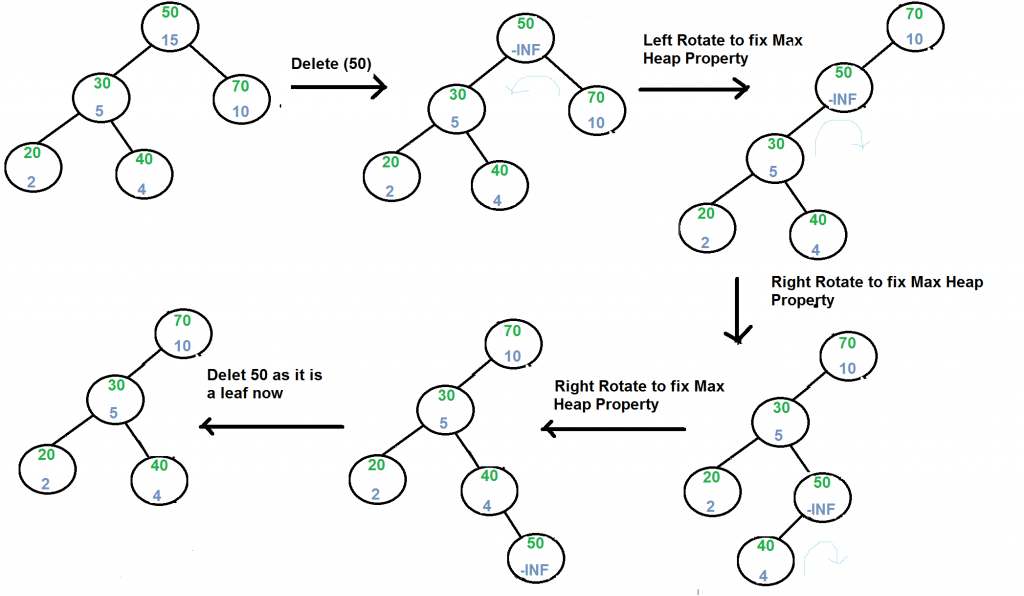
Eliminar (x):
1) Si el Node a eliminar es una hoja, elimínelo.
2) De lo contrario, reemplace la prioridad del Node con menos infinito (-INF) y realice las rotaciones apropiadas para reducir el Node a una hoja.

Consulte Implementación de Treap Search, Insert y Delete para obtener más detalles.

Referencias:
https://en.wikipedia.org/wiki/Treap
https://courses.cs.washington.edu/courses/cse326/00wi/handouts/lecture19/sld017.htm

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.