Antecedentes: ¿Qué es el centroide del árbol?
El centroide de un árbol es un Node que, si se elimina del árbol, lo dividiría en un «bosque», de modo que cualquier árbol del bosque tendría como máximo la mitad del número de vértices del árbol original.
Supongamos que hay n Nodes en el árbol. El ‘tamaño del subárbol’ para un Node es el tamaño del árbol enraizado en el Node.
Let S(v) be size of subtree rooted at node v S(v) = 1 + ∑ S(u) Here u is a child to v (adjacent and at a depth one greater than the depth of v). Centroid is a node v such that, maximum(n - S(v), S(u1), S(u2), .. S(um)) <= n/2 where ui is i'th child to v.
Encontrar el centroide
Sea T un árbol no dirigido con n Nodes. Elija cualquier Node arbitrario v en el árbol. Si v satisface la definición matemática del centroide, tenemos nuestro centroide. De lo contrario, sabemos que nuestra desigualdad matemática no se cumple, y de esto concluimos que existe alguna u adyacente a v tal que S(u) > n/2. Hacemos que u sea nuestra nueva v y recursiva.

Nunca volvemos a visitar un Node porque cuando decidimos alejarnos de él a un Node con un tamaño de subárbol mayor que n/2, declaramos que ahora pertenece al componente con Nodes menores que n/2, y nunca encontraremos nuestro centroide allí.
En cualquier caso nos estamos moviendo hacia el centroide. Además, hay un número finito de vértices en el árbol. El proceso debe detenerse, y lo hará, en el vértice deseado.
Algoritmo:
- Seleccionar Node arbitrario v
- Inicie un DFS desde v y configure los tamaños de los subárboles
- Vuelva a colocar en el Node v (o comience en cualquier v arbitraria que pertenezca al árbol)
- Comprobar la condición matemática del centroide para v
- Si se cumple la condición, devolver el Node actual como centroide
- De lo contrario, muévase al Node adyacente con el tamaño de subárbol ‘mayor’ y vuelva al paso 4
Teorema: Dado un árbol con n Nodes, el centroide siempre existe.
Prueba: A partir de nuestro enfoque del problema, queda claro que siempre podemos encontrar un centroide usando los pasos anteriores.
Complejidad del tiempo
- Seleccionar Node arbitrario v: O(1)
- DFS: O(n)
- Reposicionar a v: O(1)
- Encuentra el centroide: O(n)
Descomposición centroide:
encontrar el centroide de un árbol es parte de lo que estamos tratando de lograr aquí. Necesitamos pensar cómo podemos organizar el árbol en una estructura que disminuya la complejidad para responder a cierto ‘tipo’ de consultas.
Algoritmo
- Haga que el centroide sea la raíz de un nuevo árbol (que llamaremos ‘árbol centroide’)
- Descomponga recursivamente los árboles en el bosque resultante
- Haga que los centroides de estos árboles sean hijos del centroide que los dividió por última vez.
El árbol centroide tiene una profundidad O( log n), y se puede construir en O(n lg n), ya que podemos encontrar el centroide en O(n).
Ejemplo ilustrativo
Consideremos un árbol con 16 Nodes. La figura tiene tamaños de subárbol ya configurados mediante un DFS del Node 1.

Comenzamos en el Node 1 y vemos si se cumple la condición para el centroide. Recuerde que S(v) es el tamaño del subárbol para v.
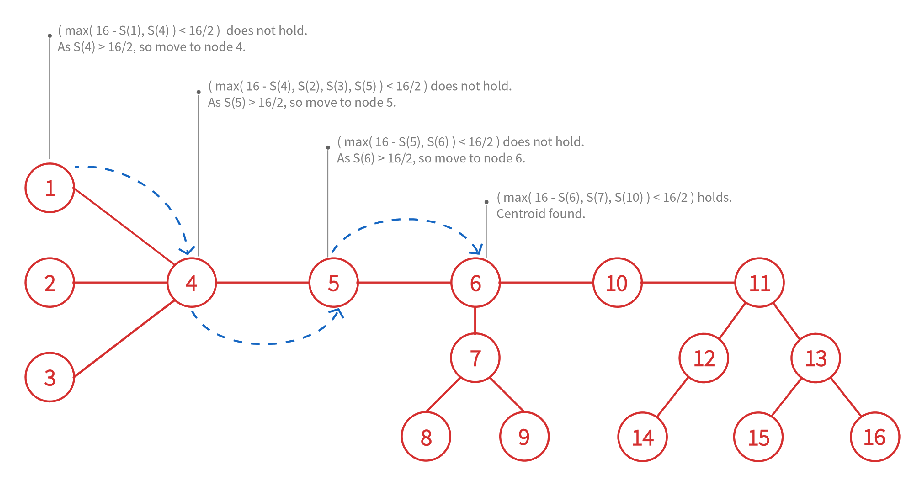
Hacemos el Node 6 como la raíz de nuestro centroide, y recurrimos a los 3 árboles del centroide del bosque en los que dividimos el árbol original.
NOTA : En la figura, los subárboles generados por un centroide han sido rodeados por una línea punteada del mismo color que el color del centroide.

Hacemos que los centroides encontrados posteriormente sean los hijos del centroide que los dividió en último lugar, y obtenemos nuestro árbol de centroides.

NOTA : Los árboles que contienen un solo elemento tienen el mismo elemento como su centroide. No hemos usado la diferenciación de colores para tales árboles, y los Nodes de las hojas los representan.
C++
// C++ program for centroid decomposition of Tree
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1025
vector<int> tree[MAXN];
vector<int> centroidTree[MAXN];
bool centroidMarked[MAXN];
/* method to add edge between to nodes of the undirected tree */
void addEdge(int u, int v)
{
tree[u].push_back(v);
tree[v].push_back(u);
}
/* method to setup subtree sizes and nodes in current tree */
void DFS(int src, bool visited[], int subtree_size[], int* n)
{
/* mark node visited */
visited[src] = true;
/* increase count of nodes visited */
*n += 1;
/* initialize subtree size for current node*/
subtree_size[src] = 1;
vector<int>::iterator it;
/* recur on non-visited and non-centroid neighbours */
for (it = tree[src].begin(); it!=tree[src].end(); it++)
if (!visited[*it] && !centroidMarked[*it])
{
DFS(*it, visited, subtree_size, n);
subtree_size[src]+=subtree_size[*it];
}
}
int getCentroid(int src, bool visited[], int subtree_size[], int n)
{
/* assume the current node to be centroid */
bool is_centroid = true;
/* mark it as visited */
visited[src] = true;
/* track heaviest child of node, to use in case node is
not centroid */
int heaviest_child = 0;
vector<int>::iterator it;
/* iterate over all adjacent nodes which are children
(not visited) and not marked as centroid to some
subtree */
for (it = tree[src].begin(); it!=tree[src].end(); it++)
if (!visited[*it] && !centroidMarked[*it])
{
/* If any adjacent node has more than n/2 nodes,
* current node cannot be centroid */
if (subtree_size[*it]>n/2)
is_centroid=false;
/* update heaviest child */
if (heaviest_child==0 ||
subtree_size[*it]>subtree_size[heaviest_child])
heaviest_child = *it;
}
/* if current node is a centroid */
if (is_centroid && n-subtree_size[src]<=n/2)
return src;
/* else recur on heaviest child */
return getCentroid(heaviest_child, visited, subtree_size, n);
}
/* function to get the centroid of tree rooted at src.
* tree may be the original one or may belong to the forest */
int getCentroid(int src)
{
bool visited[MAXN];
int subtree_size[MAXN];
/* initialize auxiliary arrays */
memset(visited, false, sizeof visited);
memset(subtree_size, 0, sizeof subtree_size);
/* variable to hold number of nodes in the current tree */
int n = 0;
/* DFS to set up subtree sizes and nodes in current tree */
DFS(src, visited, subtree_size, &n);
for (int i=1; i<MAXN; i++)
visited[i] = false;
int centroid = getCentroid(src, visited, subtree_size, n);
centroidMarked[centroid]=true;
return centroid;
}
/* function to generate centroid tree of tree rooted at src */
int decomposeTree(int root)
{
//printf("decomposeTree(%d)\n", root);
/* get centroid for current tree */
int cend_tree = getCentroid(root);
printf("%d ", cend_tree);
vector<int>::iterator it;
/* for every node adjacent to the found centroid
* and not already marked as centroid */
for (it=tree[cend_tree].begin(); it!=tree[cend_tree].end(); it++)
{
if (!centroidMarked[*it])
{
/* decompose subtree rooted at adjacent node */
int cend_subtree = decomposeTree(*it);
/* add edge between tree centroid and centroid of subtree */
centroidTree[cend_tree].push_back(cend_subtree);
centroidTree[cend_subtree].push_back(cend_tree);
}
}
/* return centroid of tree */
return cend_tree;
}
// driver function
int main()
{
/* number of nodes in the tree */
int n = 16;
/* arguments in order: node u, node v
* sequencing starts from 1 */
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
addEdge(4, 5);
addEdge(5, 6);
addEdge(6, 7);
addEdge(7, 8);
addEdge(7, 9);
addEdge(6, 10);
addEdge(10, 11);
addEdge(11, 12);
addEdge(11, 13);
addEdge(12, 14);
addEdge(13, 15);
addEdge(13, 16);
/* generates centroid tree */
decomposeTree(1);
return 0;
}
Producción :
6 4 1 2 3 5 7 8 9 11 10 12 14 13 15 16
Solicitud:
Considere el siguiente problema de ejemplo
Given a weighted tree with N nodes, find the minimum number of edges in a path of length K, or return -1 if such a path does not exist. 1 <= N <= 200000 1 <= length(i;j) <= 1000000 (integer weights) 1 <= K <= 1000000
Solución de fuerza bruta: Para cada Node, realice DFS para encontrar la distancia y el número de aristas a todos los demás Nodes
Complejidad de tiempo: O(N 2 ) Obviamente ineficiente porque N = 200000
Podemos resolver el problema anterior en tiempo O (N Log N) usando la Descomposición centroide .
- Realice la descomposición del centroide para obtener un «árbol de subárboles»
- Comience en la raíz de la descomposición, resuelva el problema para cada subárbol de la siguiente manera
- Resuelva el problema para cada «árbol hijo» del subárbol actual.
- Realice DFS desde el centroide en el subárbol actual para calcular el recuento mínimo de aristas para las rutas que incluyen el centroide
- Dos casos: centroide al final o en medio del camino
La complejidad temporal de la solución basada en la descomposición del centroide es O(n log n)
Referencia:
http://www.ugrad.cs.ubc.ca/~cs490/2014W2/pdf/jason.pdf
Este artículo es una contribución de Yash Varyani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA