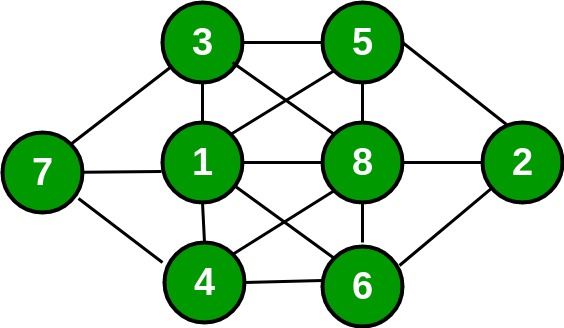
Coloque los números 1, 2, 3, 4, 5, 6, 7, 8 en los ocho círculos de la figura que se muestra a continuación, de tal manera que ningún número sea adyacente a un número que esté al lado en la secuencia. Por ejemplo, 1 no debe ser adyacente a 2 pero puede ser adyacente a 3, 4, 5, 6, 7, 8. Lo mismo ocurre con los demás.
Algoritmo Naive
El Algoritmo Naive consiste en generar todas las configuraciones posibles de números del 1 al 8 para llenar las celdas vacías. Pruebe cada configuración una por una hasta encontrar la configuración correcta.
Algoritmo de retroceso
Como todos los demás algoritmos de retrocesoproblemas, podemos resolver este problema asignando números uno por uno a las celdas vacías. Antes de asignar un número, verificamos si es seguro asignarlo. Básicamente verificamos que el mismo número no esté presente en su celda adyacente (vertical, horizontal o diagonal). Después de verificar la seguridad, asignamos el número y verificamos recursivamente si esta asignación conduce a una solución o no. Si la tarea no conduce a una solución, intentamos con el siguiente número para la celda vacía actual. Y si ninguno de los números (1 a 8) lleva a la solución, devolvemos falso.
Find row, col of an unassigned cell
If there is none, return true
For digits from 1 to 8
a) If there is no conflict for digit at row, col
assign digit to row, col and recursively try fill in rest of grid
b) If recursion successful, return true
c) Else, remove digit and try another
If all digits have been tried and nothing worked, return false
CPP
// A Backtracking program in
// C++ to solve given problem
#include <cmath>
#include <iostream>
#define N 3 // row of grid
#define M 4 // column of grid
#define UNASSIGNED -1
using namespace std;
/* Returns a boolean which indicates
whether any assigned entry within the
specified grid matches the given number. */
bool UsedInGrid(int grid[N][M], int num)
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
if (grid[i][j] == num)
return true;
}
return false;
}
/* Returns a boolean which indicates
whether it will be legal to assign
num to the given row, col location. */
bool isSafe(int grid[N][M], int row, int col, int num)
{
/* Check if 'num' is not already placed in Whole Grid*/
if (row == 0 && col == 1) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row][col + 1]) <= 1)
|| (abs(num - grid[row + 1][col]) <= 1)
|| (abs(num - grid[row + 1][col - 1]) <= 1)
|| (abs(num - grid[row + 1][col + 1]) <= 1))
return false;
}
else if (row == 0 && col == 2) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row][col - 1]) <= 1)
|| (abs(num - grid[row + 1][col]) <= 1)
|| (abs(num - grid[row + 1][col + 1]) <= 1)
|| (abs(num - grid[row + 1][col - 1]) <= 1))
return false;
}
else if (row == 1 && col == 0) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row - 1][col + 1]) <= 1)
|| (abs(num - grid[row][col + 1]) <= 1)
|| (abs(num - grid[row + 1][col + 1]) <= 1))
return false;
}
else if (row == 1 && col == 3) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row - 1][col - 1]) <= 1)
|| (abs(num - grid[row][col - 1]) <= 1)
|| (abs(num - grid[row + 1][col - 1]) <= 1))
return false;
}
else if (row == 2 && col == 1) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row - 1][col - 1]) <= 1)
|| (abs(num - grid[row - 1][col]) <= 1)
|| (abs(num - grid[row - 1][col + 1]) <= 1)
|| (abs(num - grid[row][col + 1]) <= 1))
return false;
}
else if (row == 2 && col == 2) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row][col - 1]) <= 1)
|| (abs(num - grid[row - 1][col]) <= 1)
|| (abs(num - grid[row - 1][col + 1]) <= 1)
|| (abs(num - grid[row - 1][col - 1]) <= 1))
return false;
}
else if (row == 1 && col == 1) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row][col - 1]) <= 1)
|| (abs(num - grid[row - 1][col]) <= 1)
|| (abs(num - grid[row - 1][col + 1]) <= 1)
|| (abs(num - grid[row][col + 1]) <= 1)
|| (abs(num - grid[row + 1][col + 1]) <= 1)
|| (abs(num - grid[row + 1][col]) <= 1))
return false;
}
else if (row == 1 && col == 2) {
if (UsedInGrid(grid, num)
|| (abs(num - grid[row][col - 1]) <= 1)
|| (abs(num - grid[row - 1][col]) <= 1)
|| (abs(num - grid[row + 1][col - 1]) <= 1)
|| (abs(num - grid[row][col + 1]) <= 1)
|| (abs(num - grid[row - 1][col - 1]) <= 1)
|| (abs(num - grid[row + 1][col]) <= 1))
return false;
}
return true;
}
// This function finds an entry
// in grid that is still unassigned
bool FindUnassignedLocation(int grid[N][M],
int& row, int& col)
{
for (row = 0; row < N; row++)
for (col = 0; col < M; col++) {
if (grid[row][col] == UNASSIGNED)
return true;
}
return false;
}
/* A utility function to print grid */
void printGrid(int grid[N][M])
{
for (int i = 0; i < N; i++) {
if (i == 0 || i == N - 1)
cout << " ";
for (int j = 0; j < M; j++) {
if (grid[i][j] == 0)
cout << " ";
else
cout << grid[i][j] << " ";
}
cout << endl;
}
}
/* Takes a grid and attempts to assign values to
all unassigned locations in such a way to meet
the requirements for this solution.*/
bool Solve(int grid[N][M])
{
int row, col;
// If there is no unassigned location, we are done
if (!FindUnassignedLocation(grid, row, col))
return true; // success!
// consider digits 1 to 8
for (int num = 1; num <= 8; num++) {
// if looks promising
if (isSafe(grid, row, col, num)) {
// make tentative assignment
grid[row][col] = num;
// return, if success, yay!
if (Solve(grid))
return true;
// failure, unmake & try again
grid[row][col] = UNASSIGNED;
}
}
return false; // this triggers backtracking
}
/* Driver Program to test above functions */
int main()
{
// -1 means unassigned cells
int grid[N][M] = { { 0, -1, -1, 0 },
{ -1, -1, -1, -1 },
{ 0, -1, -1, 0 } };
if (Solve(grid) == true)
printGrid(grid);
else
cout << "Not possible";
return 0;
}
3 5 7 1 8 2 4 6
Publicación traducida automáticamente
Artículo escrito por apoorv00786 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA