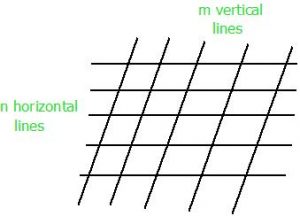
Dados dos enteros positivos n y m . La tarea es contar el número de paralelogramos que se pueden formar de cualquier tamaño cuando n líneas paralelas horizontales se cruzan con m líneas paralelas verticales.
Ejemplos:
Input : n = 3, m = 2 Output : 3 2 parallelograms of size 1x1 and 1 parallelogram of size 2x1. Input : n = 5, m = 5 Output : 100
La idea es usar Combination , cuyo estado, el número de formas de elegir k elementos de n elementos dados está dado por n C r .
Para formar un paralelogramo, necesitamos dos líneas paralelas horizontales y dos líneas paralelas verticales. Entonces, el número de formas de elegir dos líneas paralelas horizontales es n C 2 y el número de formas de elegir dos líneas paralelas verticales es m C 2 . Entonces, el número total de posibles paralelogramos será n C 2 x m C 2 .
A continuación se muestra la implementación en C++ de este enfoque:
C++
// CPP Program to find number of parallelogram when
// n horizontal parallel lines intersect m vertical
// parallel lines.
#include<bits/stdc++.h>
#define MAX 10
using namespace std;
// Find value of Binomial Coefficient
int binomialCoeff(int C[][MAX], int n, int k)
{
// Calculate value of Binomial Coefficient
// in bottom up manner
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
}
// Return number of parallelogram when n horizontal
// parallel lines intersect m vertical parallel lines.
int countParallelogram(int n, int m)
{
int C[MAX][MAX] = { 0 };
binomialCoeff(C, max(n, m), 2);
return C[n][2] * C[m][2];
}
// Driver Program
int main()
{
int n = 5, m = 5;
cout << countParallelogram(n, m) << endl;
return 0;
}
Java
// Java Program to find number of parallelogram when
// n horizontal parallel lines intersect m vertical
// parallel lines.
class GFG
{
static final int MAX = 10;
// Find value of Binomial Coefficient
static void binomialCoeff(int C[][], int n, int k)
{
// Calculate value of Binomial Coefficient
// in bottom up manner
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
// Return number of parallelogram when n horizontal
// parallel lines intersect m vertical parallel lines.
static int countParallelogram(int n, int m)
{
int C[][]=new int[MAX][MAX];
binomialCoeff(C, Math.max(n, m), 2);
return C[n][2] * C[m][2];
}
// Driver code
public static void main(String arg[])
{
int n = 5, m = 5;
System.out.println(countParallelogram(n, m));
}
}
// This code is contributed By Anant Agarwal.
Python3
# Python Program to find number of parallelogram when # n horizontal parallel lines intersect m vertical # parallel lines. MAX = 10; # Find value of Binomial Coefficient def binomialCoeff(C, n, k): # Calculate value of Binomial Coefficient # in bottom up manner for i in range(n + 1): for j in range(0, min(i, k) + 1): # Base Cases if (j == 0 or j == i): C[i][j] = 1; # Calculate value using previously # stored values else: C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; # Return number of parallelogram when n horizontal # parallel lines intersect m vertical parallel lines. def countParallelogram(n, m): C = [[0 for i in range(MAX)] for j in range(MAX)] binomialCoeff(C, max(n, m), 2); return C[n][2] * C[m][2]; # Driver code if __name__ == '__main__': n = 5; m = 5; print(countParallelogram(n, m)); # This code is contributed by 29AjayKumar
C#
// C# Program to find number of parallelogram when
// n horizontal parallel lines intersect m vertical
// parallel lines.
using System;
class GFG
{
static int MAX = 10;
// Find value of Binomial Coefficient
static void binomialCoeff(int [,]C, int n, int k)
{
// Calculate value of Binomial Coefficient
// in bottom up manner
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.Min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i, j] = 1;
// Calculate value using previously
// stored values
else
C[i, j] = C[i - 1, j - 1] + C[i - 1, j];
}
}
}
// Return number of parallelogram when n horizontal
// parallel lines intersect m vertical parallel lines.
static int countParallelogram(int n, int m)
{
int [,]C = new int[MAX, MAX];
binomialCoeff(C, Math.Max(n, m), 2);
return C[n, 2] * C[m, 2];
}
// Driver code
public static void Main()
{
int n = 5, m = 5;
Console.WriteLine(countParallelogram(n, m));
}
}
// This code is contributed By vt_m.
Javascript
<script>
// Javascript Program to find number of parallelogram when
// n horizontal parallel lines intersect m vertical
// parallel lines.
var MAX = 10;
// Find value of Binomial Coefficient
function binomialCoeff(C, n, k)
{
// Calculate value of Binomial Coefficient
// in bottom up manner
for (var i = 0; i <= n; i++)
{
for (var j = 0; j <= Math.min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
}
// Return number of parallelogram when n horizontal
// parallel lines intersect m vertical parallel lines.
function countParallelogram(n, m)
{
var C = Array.from(Array(MAX), () => Array(MAX).fill(0));
binomialCoeff(C, Math.max(n, m), 2);
return C[n][2] * C[m][2];
}
// Driver Program
var n = 5, m = 5;
document.write( countParallelogram(n, m));
// This code is contributed by rdtank.
</script>
Producción:
100
Complejidad de tiempo: O(n 2 )
Espacio auxiliar: O(n 2 )
Sugiera si alguien tiene una mejor solución que sea más eficiente en términos de espacio y tiempo.
Este artículo es una contribución de Aarti_Rathi . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.