La dirección del punto P dado desde un segmento de línea simplemente significa dadas las coordenadas de un punto P y un segmento de línea (digamos AB), y tenemos que determinar la dirección del punto P desde el segmento de línea. Eso es si el punto se encuentra a la derecha del segmento de línea oa la izquierda del segmento de línea.
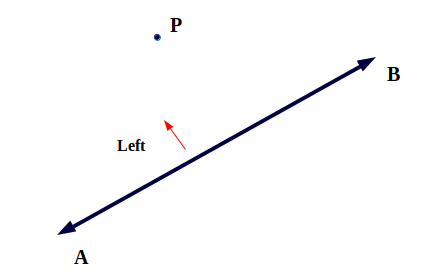
El punto puede estar detrás del segmento de línea, en ese caso asumimos una línea imaginaria al extender el segmento de línea y determinar la dirección del punto.

* Solo hay tres casos, ya sea que el punto esté en el lado izquierdo, en el lado derecho o en el segmento de línea en sí.
Este es un problema muy fundamental y se encuentra comúnmente para las direcciones en el mapa en línea .
Ejemplo : suponga que un usuario A tiene que ir al punto C en el siguiente mapa, el usuario llega primero al punto B, pero después de eso, ¿cómo sabe el usuario A que si él? tiene que girar a la derecha o a la izquierda.

Conocer la dirección de un punto a partir de un segmento de línea también actúa como un bloque de construcción para resolver problemas más complicados como:
- Intersección de segmento de línea : encontrar si dos segmentos de línea se cruzan
- Casco Convexo de un conjunto de Puntos.
El sistema de coordenadas que usaremos es un plano cartesiano, ya que la mayoría de los problemas bidimensionales usan un plano cartesiano y dado que este es un problema bidimensional.
Este problema se puede resolver usando el producto cruzado del álgebra vectorial
. El producto cruzado de dos puntos A y B es: A x * B y – A y * B x
donde A x y A y son las coordenadas x e y de A respectivamente . Análogamente, B x y B y son coordenadas x e y de B, respectivamente.
El producto cruzadotiene una propiedad interesante que se usará para determinar la dirección de un punto a partir de un segmento de línea. Es decir, el producto vectorial de dos puntos es positivo si y solo si el ángulo de esos puntos en el origen (0, 0) está en el sentido contrario a las agujas del reloj. Y a la inversa, el producto vectorial es negativo si y solo si el ángulo de esos puntos en el origen está en el sentido de las agujas del reloj.
Un ejemplo sin duda lo aclararía .
En la siguiente figura, el ángulo BOP es antihorario y el producto cruzado de BXP = 29*28 – 15*(-15) = 1037 que es positivo.

Esto nos ayuda a llegar a la conclusión de que un punto del lado derecho debe tener un producto cruzado positivo y un punto del lado izquierdo debe tener un producto cruzado negativo. También tenga en cuenta que asumimos que un punto del segmento de línea es el origen y, por lo tanto, necesitamos convertir cualquier sistema de tres puntos de modo que un punto del segmento de línea sea el origen.
El siguiente ejemplo explica el concepto :
Los tres puntos A, B y P se convirtieron en A’, B’ y P’ para hacer que A sea el origen (esto se puede hacer simplemente restando las coordenadas de A del punto P y B ), y luego calcule el producto cruzado: 59*18 – (-25)*18 = 2187
Dado que esto es positivo, el punto P está en el lado derecho del segmento de línea AB.

C++
// C++ Program to Determine Direction of Point
// from line segment
#include <iostream>
using namespace std;
// structure for point in cartesian plane.
struct point {
int x, y;
};
// constant integers for directions
const int RIGHT = 1, LEFT = -1, ZERO = 0;
int directionOfPoint(point A, point B, point P)
{
// subtracting co-ordinates of point A from
// B and P, to make A as origin
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
// Determining cross Product
int cross_product = B.x * P.y - B.y * P.x;
// return RIGHT if cross product is positive
if (cross_product > 0)
return RIGHT;
// return LEFT if cross product is negative
if (cross_product < 0)
return LEFT;
// return ZERO if cross product is zero.
return ZERO;
}
// Driver code
int main()
{
point A, B, P;
A.x = -30;
A.y = 10; // A(-30, 10)
B.x = 29;
B.y = -15; // B(29, -15)
P.x = 15;
P.y = 28; // P(15, 28)
int direction = directionOfPoint(A, B, P);
if (direction == 1)
cout << "Right Direction" << endl;
else if (direction == -1)
cout << "Left Direction" << endl;
else
cout << "Point is on the Line" << endl;
return 0;
}
Java
// Java Program to Determine Direction of Point
// from line segment
class GFG
{
// structure for point in cartesian plane.
static class point
{
int x, y;
};
// constant integers for directions
static int RIGHT = 1, LEFT = -1, ZERO = 0;
static int directionOfPoint(point A,
point B, point P)
{
// subtracting co-ordinates of point A
// from B and P, to make A as origin
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
// Determining cross Product
int cross_product = B.x * P.y - B.y * P.x;
// return RIGHT if cross product is positive
if (cross_product > 0)
return RIGHT;
// return LEFT if cross product is negative
if (cross_product < 0)
return LEFT;
// return ZERO if cross product is zero.
return ZERO;
}
// Driver code
public static void main(String[] args)
{
point A = new point(),
B = new point(), P = new point();
A.x = -30;
A.y = 10; // A(-30, 10)
B.x = 29;
B.y = -15; // B(29, -15)
P.x = 15;
P.y = 28; // P(15, 28)
int direction = directionOfPoint(A, B, P);
if (direction == 1)
System.out.println("Right Direction");
else if (direction == -1)
System.out.println("Left Direction");
else
System.out.println("Point is on the Line");
}
}
// This code is contributed
// by Princi Singh
Python3
# Python3 program to determine direction
# of point from line segment
# Structure for point in cartesian plane.
class point:
def __init__(self):
self.x = 0
self.y = 0
# Constant integers for directions
RIGHT = 1
LEFT = -1
ZERO = 0
def directionOfPoint(A, B, P):
global RIGHT, LEFT, ZERO
# Subtracting co-ordinates of
# point A from B and P, to
# make A as origin
B.x -= A.x
B.y -= A.y
P.x -= A.x
P.y -= A.y
# Determining cross Product
cross_product = B.x * P.y - B.y * P.x
# Return RIGHT if cross product is positive
if (cross_product > 0):
return RIGHT
# Return LEFT if cross product is negative
if (cross_product < 0):
return LEFT
# Return ZERO if cross product is zero
return ZERO
# Driver code
if __name__=="__main__":
A = point()
B = point()
P = point()
A.x = -30
A.y = 10 # A(-30, 10)
B.x = 29
B.y = -15 # B(29, -15)
P.x = 15
P.y = 28 # P(15, 28)
direction = directionOfPoint(A, B, P)
if (direction == 1):
print("Right Direction")
elif (direction == -1):
print("Left Direction")
else:
print("Point is on the Line")
# This code is contributed by rutvik_56
C#
// C# Program to Determine Direction of Point
// from line segment
using System;
using System.Collections.Generic;
class GFG
{
// structure for point in cartesian plane.
public class point
{
public int x, y;
};
// constant integers for directions
static int RIGHT = 1, LEFT = -1, ZERO = 0;
static int directionOfPoint(point A,
point B, point P)
{
// subtracting co-ordinates of point A
// from B and P, to make A as origin
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
// Determining cross Product
int cross_product = B.x * P.y - B.y * P.x;
// return RIGHT if cross product is positive
if (cross_product > 0)
return RIGHT;
// return LEFT if cross product is negative
if (cross_product < 0)
return LEFT;
// return ZERO if cross product is zero.
return ZERO;
}
// Driver code
public static void Main(String[] args)
{
point A = new point(),
B = new point(),
P = new point();
A.x = -30;
A.y = 10; // A(-30, 10)
B.x = 29;
B.y = -15; // B(29, -15)
P.x = 15;
P.y = 28; // P(15, 28)
int direction = directionOfPoint(A, B, P);
if (direction == 1)
Console.WriteLine("Right Direction");
else if (direction == -1)
Console.WriteLine("Left Direction");
else
Console.WriteLine("Point is on the Line");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript Program to Determine Direction of Point
// from line segment
// structure for point in cartesian plane.
class point
{
constructor()
{
this.x=0;
this.y=0;
}
}
// constant integers for directions
let RIGHT = 1, LEFT = -1, ZERO = 0;
function directionOfPoint(A,B,P)
{
// subtracting co-ordinates of point A
// from B and P, to make A as origin
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
// Determining cross Product
let cross_product = B.x * P.y - B.y * P.x;
// return RIGHT if cross product is positive
if (cross_product > 0)
return RIGHT;
// return LEFT if cross product is negative
if (cross_product < 0)
return LEFT;
// return ZERO if cross product is zero.
return ZERO;
}
// Driver code
let A = new point(),
B = new point(), P = new point();
A.x = -30;
A.y = 10; // A(-30, 10)
B.x = 29;
B.y = -15; // B(29, -15)
P.x = 15;
P.y = 28; // P(15, 28)
let direction = directionOfPoint(A, B, P);
if (direction == 1)
document.write("Right Direction<br>");
else if (direction == -1)
document.write("Left Direction");
else
document.write("Point is on the Line");
// This code is contributed by rag2127
</script>
Producción:
Right Direction
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)
Este artículo es una contribución de Shubham Rana . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA