NPDA por aceptar el lenguaje L = {anb(2n) | n>=1} U {anbn | n>=1}

Requisito previo: autómatas pushdown , aceptación de autómatas pushdown por estado final 

Problema – Diseñar un PDA no determinista que acepte el lenguaje L = { [Tex]b^{2n} [/Tex]: n>=1} U { [Tex]b^{n} [/Tex]: n>= 1}, es decir,

L = {abb, aabbbb, aaabbbbbb, aaaabbbbbbbb, ......} 
          U {ab, aabb, aaabbb, aaaabbbb, ......} 

En cada string, el número de a va seguido del doble número de b o el número de a va seguido del mismo número de b. 

Explicación: aquí, debemos mantener el orden de a y b. Es decir, todas las a vienen primero y luego todas las b. Por lo tanto, necesitamos una pila junto con el diagrama de estado. La pila mantiene el conteo de a y b. Tomaremos 2 alfabetos de pila:

 = { a, z } 

Donde,  = conjunto de todo el alfabeto de pila z = símbolo de inicio de pila 

Enfoque utilizado en la construcción de PDA: al diseñar un NPDA, cada ‘a’ viene antes de ‘b’. Si viene ‘b’ entonces

• Para 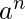 [Tex]b^{n} [/Tex]: Cada vez que aparezca ‘a’, empújelo en la pila y si ‘a’ vuelve a aparecer, también empújelo en la pila.
• Para 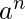 [Tex]b^{2n} [/Tex]: Cada vez que aparece ‘a’, presione ‘a’ dos veces en la pila y si ‘a’ aparece de nuevo, haga lo mismo. Cuando aparezca ‘b’ (recuerde que b viene después de ‘a’), extraiga una ‘a’ de la pila cada vez.

De modo que la pila se vacía. Si la pila está vacía, podemos decir que la PDA acepta la string. 

Funciones de transición de pila –

(q0, a, z)  (q1, az)(q0, a, z)  (q3, aaz)(q1, a, a)  (q1, aa)(q1, b, a)  (q2, ) (q2, b, a)  (q2, ) (q2, , z)  (qf1, z)   (q3 a, a)  (q3, aaa)(q3, b, a)  (q4, ) (q4, b, a)  (q4, ) (q4, , z)  (qf2, z)   

Donde, q0 = Estado inicial qf1, qf2 = Estado final  = indica operación emergente 

Entonces, este es nuestro PDA no determinista requerido para aceptar el lenguaje L ={ [Tex]b^{2n} [/Tex]: n>=1} U { [Tex]b^{n} [/Tex]: n >=1}.