Dada la array amxn mat[][] que contiene números enteros positivos. El problema es llegar a la celda (m-1, n-1) desde la celda (0, 0) siguiendo las restricciones dadas. Desde una celda (i, j) uno puede moverse ‘exactamente’ una distancia de ‘mat[i][j]’ hacia la derecha (en la misma fila) o hacia abajo (en la misma columna) solo si el movimiento lleva a una celda dentro de los límites de la array.
Por ejemplo: dado mat[1][1] = 4, entonces uno puede moverse a las celdas mat[1][5] y mat[5][1] solo si estas celdas existen en la array. Siguiendo las restricciones, compruebe si se puede llegar a la celda (m-1, n-1) desde (0, 0). 1Si uno puede alcanzar, imprima el número mínimo de celdas necesarias para cubrir durante el movimiento, de lo contrario, imprima «-1».
Ejemplos:
Input : mat[][] = { {2, 3, 2, 1, 4},
{3, 2, 5, 8, 2},
{1, 1, 2, 2, 1} }
Output : 4
The movement and cells covered are as follows:
(0, 0)->(0, 2)
|
(2, 2)->(2, 4)
Input : mat[][] = { {2, 4, 2},
{5, 3, 8},
{1, 1, 1} }
Output : 3
Algoritmo: a continuación se proporciona un enfoque de programación dinámica:
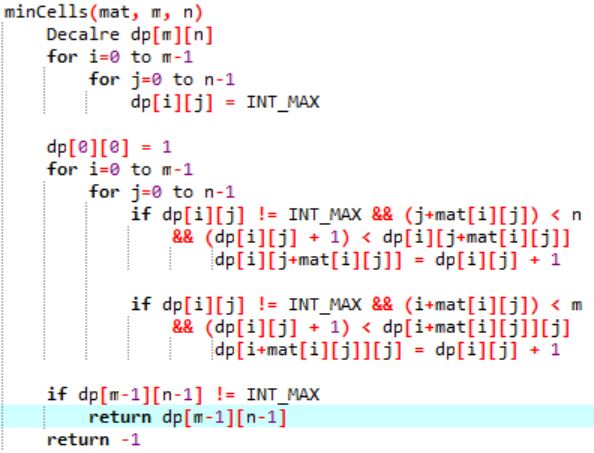
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to count minimum cells required
// to be covered to reach destination
#include <bits/stdc++.h>
using namespace std;
#define SIZE 100
// function to count minimum cells required
// to be covered to reach destination
int minCells(int mat[SIZE][SIZE], int m, int n)
{
// to store min cells required to be
// covered to reach a particular cell
int dp[m][n];
// initially no cells can be reached
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
dp[i][j] = INT_MAX;
// base case
dp[0][0] = 1;
// building up the dp[][] matrix
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// dp[i][j] != INT_MAX denotes that cell (i, j)
// can be reached from cell (0, 0) and the other
// half of the condition finds the cell on the
// right that can be reached from (i, j)
if (dp[i][j] != INT_MAX && (j + mat[i][j]) < n
&& (dp[i][j] + 1) < dp[i][j + mat[i][j]])
dp[i][j + mat[i][j]] = dp[i][j] + 1;
// the other half of the condition finds the cell
// right below that can be reached from (i, j)
if (dp[i][j] != INT_MAX && (i + mat[i][j]) < m
&& (dp[i][j] + 1) < dp[i + mat[i][j]][j])
dp[i + mat[i][j]][j] = dp[i][j] + 1;
}
}
// it true then cell (m-1, n-1) can be reached
// from cell (0, 0) and returns the minimum
// number of cells covered
if (dp[m - 1][n - 1] != INT_MAX)
return dp[m - 1][n - 1];
// cell (m-1, n-1) cannot be reached from
// cell (0, 0)
return -1;
}
// Driver program to test above
int main()
{
int mat[SIZE][SIZE] = { { 2, 3, 2, 1, 4 },
{ 3, 2, 5, 8, 2 },
{ 1, 1, 2, 2, 1 } };
int m = 3, n = 5;
cout << "Minimum number of cells = "
<< minCells(mat, m, n);
return 0;
}
Java
// Java implementation to count minimum
// cells required to be covered to reach
// destination
class MinCellsDestination
{
static final int SIZE=100;
// function to count minimum cells required
// to be covered to reach destination
static int minCells(int mat[][], int m, int n)
{
// to store min cells required to be
// covered to reach a particular cell
int dp[][] = new int[m][n];
// initially no cells can be reached
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
dp[i][j] = Integer.MAX_VALUE;
// base case
dp[0][0] = 1;
// building up the dp[][] matrix
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// dp[i][j] != INT_MAX denotes that cell
// (i, j) can be reached from cell (0, 0)
// and the other half of the condition
// finds the cell on the right that can
// be reached from (i, j)
if (dp[i][j] != Integer.MAX_VALUE &&
(j + mat[i][j]) < n && (dp[i][j] + 1)
< dp[i][j + mat[i][j]])
dp[i][j + mat[i][j]] = dp[i][j] + 1;
// the other half of the condition finds
// the cell right below that can be
// reached from (i, j)
if (dp[i][j] != Integer.MAX_VALUE &&
(i + mat[i][j]) < m && (dp[i][j] + 1)
< dp[i + mat[i][j]][j])
dp[i + mat[i][j]][j] = dp[i][j] + 1;
}
}
// it true then cell (m-1, n-1) can be reached
// from cell (0, 0) and returns the minimum
// number of cells covered
if (dp[m - 1][n - 1] != Integer.MAX_VALUE)
return dp[m - 1][n - 1];
// cell (m-1, n-1) cannot be reached from
// cell (0, 0)
return -1;
}
// Driver code
public static void main(String args[])
{
int mat[][] = { { 2, 3, 2, 1, 4 },
{ 3, 2, 5, 8, 2 },
{ 1, 1, 2, 2, 1 }};
int m = 3, n = 5;
System.out.println("Minimum number of cells" +
" = " + minCells(mat, m, n));
}
}
/* This code is contributed by Danish Kaleem */
Python3
# Python3 implementation to count minimum cells required
# to be covered to reach destination
SIZE=100
MAX=10000000
# function to count minimum cells required
# to be covered to reach destination
def minCells( mat, m, n):
# to store min cells required to be
# covered to reach a particular cell
dp=[[MAX for i in range(n)]for i in range(m)]
# initially no cells can be reached
# base case
dp[0][0] = 1
# building up the dp[][] matrix
for i in range(m):
for j in range(n):
# dp[i][j] != MAX denotes that cell (i, j)
# can be reached from cell (0, 0) and the other
# half of the condition finds the cell on the
# right that can be reached from (i, j)
if (dp[i][j] != MAX and
(j + mat[i][j]) < n and
(dp[i][j] + 1) < dp[i][j + mat[i][j]]):
dp[i][j + mat[i][j]] = dp[i][j] + 1
# the other half of the condition finds the cell
# right below that can be reached from (i, j)
if (dp[i][j] != MAX and (i + mat[i][j]) < m
and (dp[i][j] + 1) < dp[i + mat[i][j]][j]):
dp[i + mat[i][j]][j] = dp[i][j] + 1
# it true then cell (m-1, n-1) can be reached
# from cell (0, 0) and returns the minimum
# number of cells covered
if (dp[m - 1][n - 1] != MAX):
return dp[m - 1][n - 1]
# cell (m-1, n-1) cannot be reached from
# cell (0, 0)
return -1
# Driver program to test above
mat= [ [ 2, 3, 2, 1, 4 ],
[ 3, 2, 5, 8, 2 ],
[ 1, 1, 2, 2, 1 ]]
m = 3
n = 5
print("Minimum number of cells = ",
minCells(mat, m, n))
#this code is contributed by sahilshelangia
C#
// C# implementation to count minimum
// cells required to be covered to reach
// destination
using System;
class GFG {
//static int SIZE=100;
// function to count minimum cells required
// to be covered to reach destination
static int minCells(int [,]mat, int m, int n)
{
// to store min cells required to be
// covered to reach a particular cell
int [,]dp = new int[m,n];
// initially no cells can be reached
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
dp[i,j] = int.MaxValue;
// base case
dp[0,0] = 1;
// building up the dp[][] matrix
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// dp[i][j] != INT_MAX denotes that
// cell (i, j) can be reached from
// cell (0, 0) and the other half
// of the condition finds the cell
// on the right that can be reached
// from (i, j)
if (dp[i,j] != int.MaxValue &&
(j + mat[i,j]) < n && (dp[i,j] + 1)
< dp[i,j + mat[i,j]])
dp[i,j + mat[i,j]] = dp[i,j] + 1;
// the other half of the condition
// finds the cell right below that
// can be reached from (i, j)
if (dp[i,j] != int.MaxValue &&
(i + mat[i,j]) < m && (dp[i,j] + 1)
< dp[i + mat[i,j],j])
dp[i + mat[i,j],j] = dp[i,j] + 1;
}
}
// it true then cell (m-1, n-1) can be
// reached from cell (0, 0) and returns
// the minimum number of cells covered
if (dp[m - 1,n - 1] != int.MaxValue)
return dp[m - 1,n - 1];
// cell (m-1, n-1) cannot be reached from
// cell (0, 0)
return -1;
}
// Driver code
public static void Main()
{
int [,]mat = { { 2, 3, 2, 1, 4 },
{ 3, 2, 5, 8, 2 },
{ 1, 1, 2, 2, 1 } };
int m = 3, n = 5;
Console.WriteLine("Minimum number of "
+ "cells = " + minCells(mat, m, n));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// PHP implementation to count
// minimum cells required to be
// covered to reach destination
// function to count minimum
// cells required to be
// covered to reach destination
function minCells( $mat, $m, $n)
{
// to store min cells
// required to be
// covered to reach
// a particular cell
$dp =array(array());
// initially no cells
// can be reached
for($i = 0; $i < $m; $i++)
for($j = 0; $j < $n; $j++)
$dp[$i][$j] = PHP_INT_MAX;
// base case
$dp[0][0] = 1;
// building up the dp[][] matrix
for($i = 0; $i < $m; $i++)
{
for($j = 0; $j < $n; $j++)
{
// dp[i][j] != INT_MAX
// denotes that cell (i, j)
// can be reached from cell
// (0, 0) and the other half
// of the condition finds the
// cell on the right that can
// be reached from (i, j)
if ($dp[$i][$j] != PHP_INT_MAX and
($j + $mat[$i][$j]) <$n
and ($dp[$i][$j] + 1) <
$dp[$i][$j + $mat[$i][$j]])
$dp[$i][$j + $mat[$i][$j]] =
$dp[$i][$j] + 1;
// the other half of the
// condition finds the cell
// right below that can be
// reached from (i, j)
if ($dp[$i][$j] != PHP_INT_MAX and
($i + $mat[$i][$j]) < $m
and ($dp[$i][$j] + 1) <
$dp[$i +$mat[$i][$j]][$j])
$dp[$i + $mat[$i][$j]][$j] = $dp[$i][$j] + 1;
}
}
// it true then cell
// (m-1, n-1) can be reached
// from cell (0, 0) and
// returns the minimum
// number of cells covered
if ($dp[$m - 1][$n - 1] != PHP_INT_MAX)
return $dp[$m - 1][$n - 1];
// cell (m-1, n-1) cannot
// be reached from
// cell (0, 0)
return -1;
}
// Driver Code
$mat = array(array(2, 3, 2, 1, 4),
array(3, 2, 5, 8, 2),
array(1, 1, 2, 2, 1));
$m = 3; $n = 5;
echo "Minimum number of cells = "
, minCells($mat, $m, $n);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// Javascript implementation to count minimum
// cells required to be covered to reach
// destination
let SIZE=100;
// function to count minimum cells required
// to be covered to reach destination
function minCells(mat, m, n)
{
// to store min cells required to be
// covered to reach a particular cell
let dp = new Array(m);
// Loop to create 2D array using 1D array
for (var i = 0; i < dp.length; i++) {
dp[i] = new Array(2);
}
// initially no cells can be reached
for (let i = 0; i < m; i++)
for (let j = 0; j < n; j++)
dp[i][j] = Number.MAX_VALUE;
// base case
dp[0][0] = 1;
// building up the dp[][] matrix
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
// dp[i][j] != LET_MAX denotes that cell
// (i, j) can be reached from cell (0, 0)
// and the other half of the condition
// finds the cell on the right that can
// be reached from (i, j)
if (dp[i][j] != Number.MAX_VALUE &&
(j + mat[i][j]) < n && (dp[i][j] + 1)
< dp[i][j + mat[i][j]])
dp[i][j + mat[i][j]] = dp[i][j] + 1;
// the other half of the condition finds
// the cell right below that can be
// reached from (i, j)
if (dp[i][j] != Number.MAX_VALUE &&
(i + mat[i][j]) < m && (dp[i][j] + 1)
< dp[i + mat[i][j]][j])
dp[i + mat[i][j]][j] = dp[i][j] + 1;
}
}
// it true then cell (m-1, n-1) can be reached
// from cell (0, 0) and returns the minimum
// number of cells covered
if (dp[m - 1][n - 1] != Number.MAX_VALUE)
return dp[m - 1][n - 1];
// cell (m-1, n-1) cannot be reached from
// cell (0, 0)
return -1;
}
// driver function
let mat = [[ 2, 3, 2, 1, 4 ],
[ 3, 2, 5, 8, 2 ],
[ 1, 1, 2, 2, 1 ]];
let m = 3, n = 5;
document.write("Minimum number of cells" +
" = " + minCells(mat, m, n));
</script>
Minimum number of cells = 4
Tiempo Complejidad: O(m*n)
Espacio Auxiliar: O(m*n)
Este artículo es una contribución de Ayush Jauhari . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA