Dado el teclado numérico del móvil. Solo puede presionar los botones que están arriba, izquierda, derecha o abajo del botón actual. No está permitido presionar los botones de las esquinas de la fila inferior (es decir, * y #).
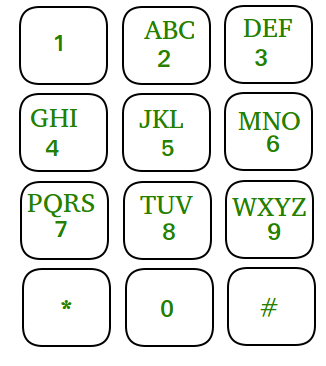
Dado un número N, encuentre el número de números posibles de longitud dada.
Ejemplos:
For N=1, number of possible numbers would be 10 (0, 1, 2, 3, …., 9) For N=2, number of possible numbers would be 36 Possible numbers: 00,08 11,12,14 22,21,23,25 and so on. If we start with 0, valid numbers will be 00, 08 (count: 2) If we start with 1, valid numbers will be 11, 12, 14 (count: 3) If we start with 2, valid numbers will be 22, 21, 23,25 (count: 4) If we start with 3, valid numbers will be 33, 32, 36 (count: 3) If we start with 4, valid numbers will be 44,41,45,47 (count: 4) If we start with 5, valid numbers will be 55,54,52,56,58 (count: 5) .................................... .................................... We need to print the count of possible numbers.
N = 1 es un caso trivial, el número de números posibles sería 10 (0, 1, 2, 3, …., 9)
Para N > 1, necesitamos comenzar desde algún botón, luego movernos a cualquiera de las cuatro direcciones ( arriba, izquierda, derecha o abajo) que lleva a un botón válido (no debe ir a *, #). Continúe haciendo esto hasta que se obtenga el número de longitud N (primer recorrido de profundidad).
Solución recursiva:
Mobile Keypad es una cuadrícula rectangular de 4X3 (4 filas y 3 columnas)
Digamos Count(i, j, N) representa el recuento de N números de longitud a partir de la posición (i, j)
If N = 1
Count(i, j, N) = 10
Else
Count(i, j, N) = Sum of all Count(r, c, N-1) where (r, c) is new
position after valid move of length 1 from current
position (i, j)
A continuación se muestra la implementación de la fórmula recursiva anterior.
C++
// A Naive Recursive C program to count number of possible numbers
// of given length
#include <stdio.h>
// left, up, right, down move from current location
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
// Returns count of numbers of length n starting from key position
// (i, j) in a numeric keyboard.
int getCountUtil(char keypad[][3], int i, int j, int n)
{
if (keypad == NULL || n <= 0)
return 0;
// From a given key, only one number is possible of length 1
if (n == 1)
return 1;
int k=0, move=0, ro=0, co=0, totalCount = 0;
// move left, up, right, down from current location and if
// new location is valid, then get number count of length
// (n-1) from that new position and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#')
{
totalCount += getCountUtil(keypad, ro, co, n-1);
}
}
return totalCount;
}
// Return count of all possible numbers of length n
// in a given numeric keyboard
int getCount(char keypad[][3], int n)
{
// Base cases
if (keypad == NULL || n <= 0)
return 0;
if (n == 1)
return 10;
int i=0, j=0, totalCount = 0;
for (i=0; i<4; i++) // Loop on keypad row
{
for (j=0; j<3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#')
{
// Get count when number is starting from key
// position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
// Driver program to test above function
int main(int argc, char *argv[])
{
char keypad[4][3] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
printf("Count for numbers of length %d: %dn \n", 1, getCount(keypad, 1));
printf("Count for numbers of length %d: %dn \n", 2, getCount(keypad, 2));
printf("Count for numbers of length %d: %dn \n", 3, getCount(keypad, 3));
printf("Count for numbers of length %d: %dn \n", 4, getCount(keypad, 4));
printf("Count for numbers of length %d: %dn", 5, getCount(keypad, 5));
return 0;
}
Java
// A Naive Recursive Java program
// to count number of possible
// numbers of given length
class GfG
{
// left, up, right, down
// move from current location
static int row[] = {0, 0, -1, 0, 1};
static int col[] = {0, -1, 0, 1, 0};
// Returns count of numbers of length
// n starting from key position
// (i, j) in a numeric keyboard.
static int getCountUtil(char keypad[][],
int i, int j, int n)
{
if (keypad == null || n <= 0)
return 0;
// From a given key, only one
// number is possible of length 1
if (n == 1)
return 1;
int k = 0, move = 0, ro = 0, co = 0, totalCount = 0;
// move left, up, right, down
// from current location and if
// new location is valid, then
// get number count of length
// (n-1) from that new position
// and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#')
{
totalCount += getCountUtil(keypad, ro, co, n - 1);
}
}
return totalCount;
}
// Return count of all possible numbers of length n
// in a given numeric keyboard
static int getCount(char keypad[][], int n)
{
// Base cases
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
int i = 0, j = 0, totalCount = 0;
for (i = 0; i < 4; i++) // Loop on keypad row
{
for (j=0; j<3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#')
{
// Get count when number is starting from key
// position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
// Driver code
public static void main(String[] args)
{
char keypad[][] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
System.out.printf("Count for numbers of"+
" length %d: %d", 1, getCount(keypad, 1));
System.out.printf("\nCount for numbers of" +
" length %d: %d", 2, getCount(keypad, 2));
System.out.printf("\nCount for numbers of" +
" length %d: %d", 3, getCount(keypad, 3));
System.out.printf("\nCount for numbers of" +
" length %d: %d", 4, getCount(keypad, 4));
System.out.printf("\nCount for numbers of" +
" length %d: %d", 5, getCount(keypad, 5));
}
}
// This code has been contributed by 29AjayKumar
Python3
# A Naive Recursive Python program to count number of possible numbers
# of given length
# left, up, right, down move from current location
row = [0, 0, -1, 0, 1]
col = [0, -1, 0, 1, 0]
# Returns count of numbers of length n starting from key position
# (i, j) in a numeric keyboard.
def getCountUtil(keypad, i, j, n):
if (keypad == None or n <= 0):
return 0
# From a given key, only one number is possible of length 1
if (n == 1):
return 1
k = 0
move = 0
ro = 0
co = 0
totalCount = 0
# move left, up, right, down from current location and if
# new location is valid, then get number count of length
# (n-1) from that new position and add in count obtained so far
for move in range(5):
ro = i + row[move]
co = j + col[move]
if (ro >= 0 and ro <= 3 and co >= 0 and co <= 2 and
keypad[ro][co] != '*' and keypad[ro][co] != '#'):
totalCount += getCountUtil(keypad, ro, co, n - 1)
return totalCount
# Return count of all possible numbers of length n
# in a given numeric keyboard
def getCount(keypad, n):
# Base cases
if (keypad == None or n <= 0):
return 0
if (n == 1):
return 10
i = 0
j = 0
totalCount = 0
for i in range(4): # Loop on keypad row
for j in range(3): # Loop on keypad column
# Process for 0 to 9 digits
if (keypad[i][j] != '*' and keypad[i][j] != '#'):
# Get count when number is starting from key
# position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n)
return totalCount
# Driver code
keypad = [['1', '2', '3'],
['4', '5', '6'],
['7', '8', '9'],
['*', '0', '#']]
print("Count for numbers of length 1:", getCount(keypad, 1))
print("Count for numbers of length 2:", getCount(keypad, 2))
print("Count for numbers of length 3:", getCount(keypad, 3))
print("Count for numbers of length 4:", getCount(keypad, 4))
print("Count for numbers of length 5:", getCount(keypad, 5))
# This code is contributed by subhammahato348
C#
// A Naive Recursive C# program
// to count number of possible
// numbers of given length
using System;
class GfG
{
// left, up, right, down
// move from current location
static int []row = {0, 0, -1, 0, 1};
static int []col = {0, -1, 0, 1, 0};
// Returns count of numbers of length
// n starting from key position
// (i, j) in a numeric keyboard.
static int getCountUtil(char [,]keypad,
int i, int j, int n)
{
if (keypad == null || n <= 0)
return 0;
// From a given key, only one
// number is possible of length 1
if (n == 1)
return 1;
int k = 0, move = 0, ro = 0, co = 0, totalCount = 0;
// move left, up, right, down
// from current location and if
// new location is valid, then
// get number count of length
// (n-1) from that new position
// and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro,co] != '*' && keypad[ro,co] != '#')
{
totalCount += getCountUtil(keypad, ro, co, n - 1);
}
}
return totalCount;
}
// Return count of all possible numbers of length n
// in a given numeric keyboard
static int getCount(char [,]keypad, int n)
{
// Base cases
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
int i = 0, j = 0, totalCount = 0;
for (i = 0; i < 4; i++) // Loop on keypad row
{
for (j = 0; j < 3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i, j] != '*' && keypad[i, j] != '#')
{
// Get count when number is starting from key
// position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
// Driver code
public static void Main()
{
char [,]keypad = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
Console.Write("Count for numbers of"+
" length {0}: {1}", 1, getCount(keypad, 1));
Console.Write("\nCount for numbers of" +
"length {0}: {1}", 2, getCount(keypad, 2));
Console.Write("\nCount for numbers of" +
"length {0}: {1}", 3, getCount(keypad, 3));
Console.Write("\nCount for numbers of" +
"length {0}: {1}", 4, getCount(keypad, 4));
Console.Write("\nCount for numbers of" +
"length {0}: {1}", 5, getCount(keypad, 5));
}
}
/* This code contributed by PrinciRaj1992 */
PHP
<?php
// A Naive Recursive PHP program
// to count number of possible
// numbers of given length
// left, up, right, down
// move from current location
// static $row = array(0, 0, -1, 0, 1);
//static $col = array(0, -1, 0, 1, 0);
// Returns count of numbers of length
// n starting from key position
// (i, j) in a numeric keyboard.
function getCountUtil($keypad,
$i, $j, $n)
{
static $row= array(0,0,-1,0,1);
static $col= array(0,-1,0,1,0);
if ($keypad == null || $n <= 0)
return 0;
// From a given key, only one
// number is possible of length 1
if ($n == 1)
return 1;
$k = 0; $move = 0; $ro = 0; $co = 0; $totalCount = 0;
// move left, up, right, down
// from current location and if
// new location is valid, then
// get number count of length
// (n-1) from that new position
// and add in count obtained so far
for ($move = 0; $move < 5; $move++)
{
$ro = $i + $row[$move];
$co = $j + $col[$move];
if ($ro >= 0 && $ro <= 3 && $co >=0 && $co <= 2 &&
$keypad[$ro][$co] != '*' && $keypad[$ro][$co] != '#')
{
$totalCount += getCountUtil($keypad, $ro, $co, $n - 1);
}
}
return $totalCount;
}
// Return count of all possible numbers of length n
// in a given numeric keyboard
function getCount($keypad, $n)
{
// Base cases
if ($keypad == null || $n <= 0)
return 0;
if ($n == 1)
return 10;
$i = 0; $j = 0; $totalCount = 0;
for ($i = 0; $i < 4; $i++) // Loop on keypad row
{
for ($j = 0; $j < 3; $j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if ($keypad[$i][$j] != '*' && $keypad[$i][$j] != '#')
{
// Get count when number is starting from key
// position (i, j) and add in count obtained so far
$totalCount += getCountUtil($keypad, $i, $j, $n);
}
}
}
return $totalCount;
}
// Driver code
{
$keypad = array(array('1','2','3'),
array('4','5','6'),
array('7','8','9'),
array('*','0','#'));
echo("Count for numbers of"." length". getCount($keypad, 1));
echo("\nCount for numbers of" .
" length ". getCount($keypad, 2));
echo("\nCount for numbers of" .
" length ".getCount($keypad, 3));
echo("\nCount for numbers of" .
" length ".getCount($keypad, 4));
echo("\nCount for numbers of" .
" length ".getCount($keypad, 5));
}
// This code has been contributed by Code_Mech.
Javascript
<script>
// A Naive Recursive Javascript program
// to count number of possible
// numbers of given length
// left, up, right, down
// move from current location
let row=[0, 0, -1, 0, 1];
let col=[0, -1, 0, 1, 0];
// Returns count of numbers of length
// n starting from key position
// (i, j) in a numeric keyboard.
function getCountUtil(keypad,i,j,n)
{
if (keypad == null || n <= 0)
{return 0;}
// From a given key, only one
// number is possible of length 1
if (n == 1)
return 1;
let k = 0, move = 0, ro = 0, co = 0, totalCount = 0;
// move left, up, right, down
// from current location and if
// new location is valid, then
// get number count of length
// (n-1) from that new position
// and add in count obtained so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#')
{
totalCount += getCountUtil(keypad, ro, co, n - 1);
}
}
return totalCount;
}
// Return count of all possible numbers of length n
// in a given numeric keyboard
function getCount(keypad,n)
{
// Base cases
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
let i = 0, j = 0, totalCount = 0;
for (i = 0; i < 4; i++) // Loop on keypad row
{
for (j=0; j<3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#')
{
// Get count when number is starting from key
// position (i, j) and add in count obtained so far
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
// Driver code
let keypad=[['1','2','3'],['4','5','6'],['7','8','9'],['*','0','#']];
document.write("Count for numbers of"+
" length ", 1,": ", getCount(keypad, 1));
document.write("<br>Count for numbers of" +
"length ", 2,": ", getCount(keypad, 2));
document.write("<br>Count for numbers of" +
"length ", 3,": ", getCount(keypad, 3));
document.write("<br>Count for numbers of" +
"length ", 4,": ", getCount(keypad, 4));
document.write("<br>Count for numbers of" +
"length ", 5,": ", getCount(keypad, 5));
// This code is contributed by avanitrachhadiya2155
</script>
Count for numbers of length 1: 10n Count for numbers of length 2: 36n Count for numbers of length 3: 138n Count for numbers of length 4: 532n Count for numbers of length 5: 2062n
Programación dinámica
Hay muchos recorridos repetidos en caminos más pequeños (recorrido para N más pequeño) para encontrar todos los caminos más largos posibles (recorrido para N más grande). Consulte los siguientes dos diagramas, por ejemplo. En este recorrido, para N = 4 desde dos posiciones iniciales (botones ‘4’ y ‘8’), podemos ver que hay pocos recorridos repetidos para N = 2 (por ejemplo, 4 -> 1, 6 -> 3, 8 -> 9, 8 -> 7, etc.).
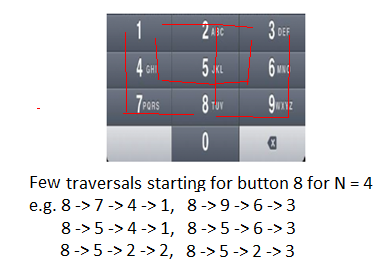
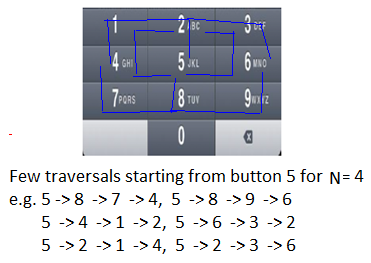
Dado que el problema tiene ambas propiedades: subestructura óptima y subproblemas superpuestos , se puede resolver de manera eficiente mediante programación dinámica.
A continuación se muestra el programa para la implementación de la programación dinámica.
C++
// A Dynamic Programming based C program to count number of
// possible numbers of given length
#include <stdio.h>
// Return count of all possible numbers of length n
// in a given numeric keyboard
int getCount(char keypad[][3], int n)
{
if(keypad == NULL || n <= 0)
return 0;
if(n == 1)
return 10;
// left, up, right, down move from current location
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
// taking n+1 for simplicity - count[i][j] will store
// number count starting with digit i and length j
int count[10][n+1];
int i=0, j=0, k=0, move=0, ro=0, co=0, num = 0;
int nextNum=0, totalCount = 0;
// count numbers starting with digit i and of lengths 0 and 1
for (i=0; i<=9; i++)
{
count[i][0] = 0;
count[i][1] = 1;
}
// Bottom up - Get number count of length 2, 3, 4, ... , n
for (k=2; k<=n; k++)
{
for (i=0; i<4; i++) // Loop on keypad row
{
for (j=0; j<3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' && keypad[i][j] != '#')
{
// Here we are counting the numbers starting with
// digit keypad[i][j] and of length k keypad[i][j]
// will become 1st digit, and we need to look for
// (k-1) more digits
num = keypad[i][j] - '0';
count[num][k] = 0;
// move left, up, right, down from current location
// and if new location is valid, then get number
// count of length (k-1) from that new digit and
// add in count we found so far
for (move=0; move<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#')
{
nextNum = keypad[ro][co] - '0';
count[num][k] += count[nextNum][k-1];
}
}
}
}
}
}
// Get count of all possible numbers of length "n" starting
// with digit 0, 1, 2, ..., 9
totalCount = 0;
for (i=0; i<=9; i++)
totalCount += count[i][n];
return totalCount;
}
// Driver program to test above function
int main(int argc, char *argv[])
{
char keypad[4][3] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
printf("Count for numbers of length %d: %dn", 1, getCount(keypad, 1));
printf("\nCount for numbers of length %d: %dn", 2, getCount(keypad, 2));
printf("\nCount for numbers of length %d: %dn", 3, getCount(keypad, 3));
printf("\nCount for numbers of length %d: %dn", 4, getCount(keypad, 4));
printf("\nCount for numbers of length %d: %dn", 5, getCount(keypad, 5));
return 0;
}
Java
// A Dynamic Programming based Java program to
// count number of possible numbers of given length
class GFG
{
// Return count of all possible numbers of length n
// in a given numeric keyboard
static int getCount(char keypad[][], int n)
{
if(keypad == null || n <= 0)
return 0;
if(n == 1)
return 10;
// left, up, right, down move from current location
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
// taking n+1 for simplicity - count[i][j] will store
// number count starting with digit i and length j
int [][]count = new int[10][n + 1];
int i = 0, j = 0, k = 0, move = 0,
ro = 0, co = 0, num = 0;
int nextNum = 0, totalCount = 0;
// count numbers starting with digit i
// and of lengths 0 and 1
for (i = 0; i <= 9; i++)
{
count[i][0] = 0;
count[i][1] = 1;
}
// Bottom up - Get number count of length 2, 3, 4, ... , n
for (k = 2; k <= n; k++)
{
for (i = 0; i < 4; i++) // Loop on keypad row
{
for (j = 0; j < 3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' &&
keypad[i][j] != '#')
{
// Here we are counting the numbers starting with
// digit keypad[i][j] and of length k keypad[i][j]
// will become 1st digit, and we need to look for
// (k-1) more digits
num = keypad[i][j] - '0';
count[num][k] = 0;
// move left, up, right, down from current location
// and if new location is valid, then get number
// count of length (k-1) from that new digit and
// add in count we found so far
for (move = 0; move < 5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >= 0 &&
co <= 2 && keypad[ro][co] != '*' &&
keypad[ro][co] != '#')
{
nextNum = keypad[ro][co] - '0';
count[num][k] += count[nextNum][k - 1];
}
}
}
}
}
}
// Get count of all possible numbers of length "n"
// starting with digit 0, 1, 2, ..., 9
totalCount = 0;
for (i = 0; i <= 9; i++)
totalCount += count[i][n];
return totalCount;
}
// Driver Code
public static void main(String[] args)
{
char keypad[][] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
System.out.printf("Count for numbers of length %d: %d\n", 1,
getCount(keypad, 1));
System.out.printf("Count for numbers of length %d: %d\n", 2,
getCount(keypad, 2));
System.out.printf("Count for numbers of length %d: %d\n", 3,
getCount(keypad, 3));
System.out.printf("Count for numbers of length %d: %d\n", 4,
getCount(keypad, 4));
System.out.printf("Count for numbers of length %d: %d\n", 5,
getCount(keypad, 5));
}
}
// This code is contributed by Rajput-Ji
Python3
# A Dynamic Programming based C program to count number of
# possible numbers of given length
# Return count of all possible numbers of length n
# in a given numeric keyboard
def getCount(keypad, n):
if (keypad == None or n <= 0):
return 0
if (n == 1):
return 10
# left, up, right, down move from current location
row = [0, 0, -1, 0, 1]
col = [0, -1, 0, 1, 0]
# taking n+1 for simplicity - count[i][j] will store
# number count starting with digit i and length j
# count[10][n+1]
count = [[0]*(n + 1)]*10
i = 0
j = 0
k = 0
move = 0
ro = 0
co = 0
num = 0
nextNum = 0
totalCount = 0
# count numbers starting with
# digit i and of lengths 0 and 1
for i in range(10):
count[i][0] = 0
count[i][1] = 1
# Bottom up - Get number
# count of length 2, 3, 4, ... , n
for k in range(2, n + 1):
for i in range(4): # Loop on keypad row
for j in range(3): # Loop on keypad column
# Process for 0 to 9 digits
if (keypad[i][j] != '*' and keypad[i][j] != '#'):
# Here we are counting the numbers starting with
# digit keypad[i][j] and of length k keypad[i][j]
# will become 1st digit, and we need to look for
# (k-1) more digits
num = ord(keypad[i][j]) - 48
count[num][k] = 0
# move left, up, right, down from current location
# and if new location is valid, then get number
# count of length (k-1) from that new digit and
# add in count we found so far
for move in range(5):
ro = i + row[move]
co = j + col[move]
if (ro >= 0 and ro <= 3 and co >= 0 and co <= 2 and
keypad[ro][co] != '*' and keypad[ro][co] != '#'):
nextNum = ord(keypad[ro][co]) - 48
count[num][k] += count[nextNum][k - 1]
# Get count of all possible numbers of length "n" starting
# with digit 0, 1, 2, ..., 9
totalCount = 0
for i in range(10):
totalCount += count[i][n]
return totalCount
# Driver code
if __name__ == "__main__":
keypad = [['1','2','3'],
['4','5','6'],
['7','8','9'],
['*','0','#']]
print("Count for numbers of length", 1, ":", getCount(keypad, 1))
print("Count for numbers of length", 2, ":", getCount(keypad, 2))
print("Count for numbers of length", 3, ":", getCount(keypad, 3))
print("Count for numbers of length", 4, ":", getCount(keypad, 4))
print("Count for numbers of length", 5, ":", getCount(keypad, 5))
# This code is contributed by subhammahato348
C#
// A Dynamic Programming based C# program to
// count number of possible numbers of given Length
using System;
class GFG
{
// Return count of all possible numbers of Length n
// in a given numeric keyboard
static int getCount(char [,]keypad, int n)
{
if(keypad == null || n <= 0)
return 0;
if(n == 1)
return 10;
// left, up, right, down move
// from current location
int []row = {0, 0, -1, 0, 1};
int []col = {0, -1, 0, 1, 0};
// taking n+1 for simplicity - count[i,j]
// will store number count starting with
// digit i and.Length j
int [,]count = new int[10,n + 1];
int i = 0, j = 0, k = 0, move = 0,
ro = 0, co = 0, num = 0;
int nextNum = 0, totalCount = 0;
// count numbers starting with digit i
// and of.Lengths 0 and 1
for (i = 0; i <= 9; i++)
{
count[i, 0] = 0;
count[i, 1] = 1;
}
// Bottom up - Get number count of
// Length 2, 3, 4, ... , n
for (k = 2; k <= n; k++)
{
for (i = 0; i < 4; i++) // Loop on keypad row
{
for (j = 0; j < 3; j++) // Loop on keypad column
{
// Process for 0 to 9 digits
if (keypad[i, j] != '*' &&
keypad[i, j] != '#')
{
// Here we are counting the numbers starting with
// digit keypad[i,j] and of.Length k keypad[i,j]
// will become 1st digit, and we need to look for
// (k-1) more digits
num = keypad[i, j] - '0';
count[num, k] = 0;
// move left, up, right, down from current location
// and if new location is valid, then get number
// count of.Length (k-1) from that new digit and
//.Add in count we found so far
for (move = 0; move < 5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >= 0 &&
co <= 2 && keypad[ro, co] != '*' &&
keypad[ro, co] != '#')
{
nextNum = keypad[ro, co] - '0';
count[num, k] += count[nextNum, k - 1];
}
}
}
}
}
}
// Get count of all possible numbers of.Length "n"
// starting with digit 0, 1, 2, ..., 9
totalCount = 0;
for (i = 0; i <= 9; i++)
totalCount += count[i, n];
return totalCount;
}
// Driver Code
public static void Main(String[] args)
{
char [,]keypad = {{'1', '2', '3'},
{'4', '5', '6'},
{'7', '8', '9'},
{'*', '0', '#'}};
Console.Write("Count for numbers of.Length {0}: {1}\n", 1,
getCount(keypad, 1));
Console.Write("Count for numbers of.Length {0}: {1}\n", 2,
getCount(keypad, 2));
Console.Write("Count for numbers of.Length {0}: {1}\n", 3,
getCount(keypad, 3));
Console.Write("Count for numbers of.Length {0}: {1}\n", 4,
getCount(keypad, 4));
Console.Write("Count for numbers of.Length {0}: {1}\n", 5,
getCount(keypad, 5));
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// A Dynamic Programming based Javascript program to
// count number of possible numbers of given length
// Return count of all possible numbers of length n
// in a given numeric keyboard
function getCount(keypad, n)
{
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return 10;
// left, up, right, down move
// from current location
let row = [ 0, 0, -1, 0, 1 ];
let col = [ 0, -1, 0, 1, 0 ];
// Taking n+1 for simplicity - count[i][j]
// will store number count starting with
// digit i and length j
let count = new Array(10);
for(let i = 0; i < 10; i++)
{
count[i] = new Array(n + 1);
for(let j = 0; j < n + 1; j++)
{
count[i][j] = 0;
}
}
let i = 0, j = 0, k = 0, move = 0,
ro = 0, co = 0, num = 0;
let nextNum = 0, totalCount = 0;
// count numbers starting with digit i
// and of lengths 0 and 1
for(i = 0; i <= 9; i++)
{
count[i][0] = 0;
count[i][1] = 1;
}
// Bottom up - Get number count
// of length 2, 3, 4, ... , n
for(k = 2; k <= n; k++)
{
// Loop on keypad row
for(i = 0; i < 4; i++)
{
// Loop on keypad column
for(j = 0; j < 3; j++)
{
// Process for 0 to 9 digits
if (keypad[i][j] != '*' &&
keypad[i][j] != '#')
{
// Here we are counting the numbers starting with
// digit keypad[i][j] and of length k keypad[i][j]
// will become 1st digit, and we need to look for
// (k-1) more digits
num = keypad[i][j].charCodeAt(0) -
'0'.charCodeAt(0);
count[num][k] = 0;
// Move left, up, right, down from current location
// and if new location is valid, then get number
// count of length (k-1) from that new digit and
// add in count we found so far
for(move = 0; move < 5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >= 0 &&
co <= 2 && keypad[ro][co] != '*' &&
keypad[ro][co] != '#')
{
nextNum = keypad[ro][co].charCodeAt(0) -
'0'.charCodeAt(0);
count[num][k] += count[nextNum][k - 1];
}
}
}
}
}
}
// Get count of all possible numbers of length "n"
// starting with digit 0, 1, 2, ..., 9
totalCount = 0;
for(i = 0; i <= 9; i++)
totalCount += count[i][n];
return totalCount;
}
// Driver Code
let keypad = [ [ '1','2','3' ],
[ '4','5','6' ],
[ '7','8','9' ],
[ '*','0','#' ] ];
document.write("Count for numbers of length " +
1 + " : " + getCount(keypad, 1) + "<br>")
document.write("Count for numbers of length " +
2 + " : " + getCount(keypad, 2) + "<br>")
document.write("Count for numbers of length " +
3 + " : " + getCount(keypad, 3) + "<br>")
document.write("Count for numbers of length " +
4 + " : " + getCount(keypad, 4) + "<br>")
document.write("Count for numbers of length " +
5 + " : " + getCount(keypad, 5) + "<br>")
// This code is contributed by rag2127
</script>
Count for numbers of length 1: 10n Count for numbers of length 2: 36n Count for numbers of length 3: 138n Count for numbers of length 4: 532n Count for numbers of length 5: 2062n
Una solución optimizada para el espacio:
El enfoque de programación dinámica anterior también se ejecuta en tiempo O(n) y requiere espacio auxiliar O(n), ya que solo un bucle for se ejecuta n veces, otro bucle for se ejecuta durante un tiempo constante. Podemos ver que la iteración n necesita datos de la iteración (n-1) solamente, por lo que no necesitamos conservar los datos de las iteraciones anteriores. Podemos tener un enfoque de programación dinámica eficiente en el espacio con solo dos arrays de tamaño 10. Gracias a Nik por sugerir esta solución.
C++
// A Space Optimized C++ program to count number of possible numbers
// of given length
#include <bits/stdc++.h>
using namespace std;
// Return count of all possible numbers of length n
// in a given numeric keyboard
int getCount(char keypad[][3], int n)
{
if (keypad == NULL || n <= 0)
return 0;
if (n == 1)
return 10;
// odd[i], even[i] arrays represent count of numbers starting
// with digit i for any length j
int odd[10], even[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1; // for j = 1
for (j = 2; j <= n; j++) // Bottom Up calculation from j = 2 to n
{
useOdd = 1 - useOdd;
// Here we are explicitly writing lines for each number 0
// to 9. But it can always be written as DFS on 4X3 grid
// using row, column array valid moves
if (useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] + odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] + odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] + odd[8] + odd[6];
even[6] = odd[6] + odd[3] + odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] + odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] + even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] + even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] + even[8] + even[6];
odd[6] = even[6] + even[3] + even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] + even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
// Get count of all possible numbers of length "n" starting
// with digit 0, 1, 2, ..., 9
totalCount = 0;
if (useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
// Driver program to test above function
int main()
{
char keypad[4][3] = {{'1', '2', '3'},
{'4', '5', '6'},
{'7', '8', '9'},
{'*', '0', '#'}};
cout << "Count for numbers of length 1: " << getCount(keypad, 1) << endl;
cout << "Count for numbers of length 2: " << getCount(keypad, 2) << endl;
cout << "Count for numbers of length 3: " << getCount(keypad, 3) << endl;
cout << "Count for numbers of length 4: " << getCount(keypad, 4) << endl;
cout << "Count for numbers of length 5: " << getCount(keypad, 5) << endl;
return 0;
}
//This code is contributed by Mayank Tyagi
C
// A Space Optimized C program to count number of possible numbers
// of given length
#include <stdio.h>
// Return count of all possible numbers of length n
// in a given numeric keyboard
int getCount(char keypad[][3], int n)
{
if(keypad == NULL || n <= 0)
return 0;
if(n == 1)
return 10;
// odd[i], even[i] arrays represent count of numbers starting
// with digit i for any length j
int odd[10], even[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i=0; i<=9; i++)
odd[i] = 1; // for j = 1
for (j=2; j<=n; j++) // Bottom Up calculation from j = 2 to n
{
useOdd = 1 - useOdd;
// Here we are explicitly writing lines for each number 0
// to 9. But it can always be written as DFS on 4X3 grid
// using row, column array valid moves
if(useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] + odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] + odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] + odd[8] + odd[6];
even[6] = odd[6] + odd[3] + odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] + odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] + even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] + even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] + even[8] + even[6];
odd[6] = even[6] + even[3] + even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] + even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
// Get count of all possible numbers of length "n" starting
// with digit 0, 1, 2, ..., 9
totalCount = 0;
if(useOdd == 1)
{
for (i=0; i<=9; i++)
totalCount += even[i];
}
else
{
for (i=0; i<=9; i++)
totalCount += odd[i];
}
return totalCount;
}
// Driver program to test above function
int main()
{
char keypad[4][3] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}
};
printf("Count for numbers of length %d: %dn", 1, getCount(keypad, 1));
printf("Count for numbers of length %d: %dn", 2, getCount(keypad, 2));
printf("Count for numbers of length %d: %dn", 3, getCount(keypad, 3));
printf("Count for numbers of length %d: %dn", 4, getCount(keypad, 4));
printf("Count for numbers of length %d: %dn", 5, getCount(keypad, 5));
return 0;
}
Java
// A Space Optimized Java program to
// count number of possible numbers
// of given length
class GFG
{
// Return count of all possible numbers of
// length n in a given numeric keyboard
static int getCount(char keypad[][], int n)
{
if(keypad == null || n <= 0)
return 0;
if(n == 1)
return 10;
// odd[i], even[i] arrays represent count of
// numbers starting with digit i for any length j
int []odd = new int[10];
int []even = new int[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1; // for j = 1
// Bottom Up calculation from j = 2 to n
for (j = 2; j <= n; j++)
{
useOdd = 1 - useOdd;
// Here we are explicitly writing lines
// for each number 0 to 9. But it can always be
// written as DFS on 4X3 grid using row,
// column array valid moves
if(useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] +
odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] +
odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] +
odd[8] + odd[6];
even[6] = odd[6] + odd[3] +
odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] +
odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] +
even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] +
even[8] + even[6];
odd[6] = even[6] + even[3] +
even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] +
even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
// Get count of all possible numbers of
// length "n" starting with digit 0, 1, 2, ..., 9
totalCount = 0;
if(useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
// Driver Code
public static void main(String[] args)
{
char keypad[][] = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
System.out.printf("Count for numbers of length %d: %d\n", 1,
getCount(keypad, 1));
System.out.printf("Count for numbers of length %d: %d\n", 2,
getCount(keypad, 2));
System.out.printf("Count for numbers of length %d: %d\n", 3,
getCount(keypad, 3));
System.out.printf("Count for numbers of length %d: %d\n", 4,
getCount(keypad, 4));
System.out.printf("Count for numbers of length %d: %d\n", 5,
getCount(keypad, 5));
}
}
// This code is contributed by PrinciRaj1992
Python3
# A Space Optimized Python program to count
# number of possible numbers
# of given length
# Return count of all possible numbers
# of length n
# in a given numeric keyboard
def getCount(keypad, n):
if(not keypad or n <= 0):
return 0
if(n == 1):
return 10
# odd[i], even[i] arrays represent
# count of numbers starting
# with digit i for any length j
odd = [0]*10
even = [0]*10
i = 0
j = 0
useOdd = 0
totalCount = 0
for i in range(10):
odd[i] = 1 # for j = 1
for j in range(2,n+1): # Bottom Up calculation from j = 2 to n
useOdd = 1 - useOdd
# Here we are explicitly writing lines for each number 0
# to 9. But it can always be written as DFS on 4X3 grid
# using row, column array valid moves
if(useOdd == 1):
even[0] = odd[0] + odd[8]
even[1] = odd[1] + odd[2] + odd[4]
even[2] = odd[2] + odd[1] + odd[3] + odd[5]
even[3] = odd[3] + odd[2] + odd[6]
even[4] = odd[4] + odd[1] + odd[5] + odd[7]
even[5] = odd[5] + odd[2] + odd[4] + odd[8] + odd[6]
even[6] = odd[6] + odd[3] + odd[5] + odd[9]
even[7] = odd[7] + odd[4] + odd[8]
even[8] = odd[8] + odd[0] + odd[5] + odd[7] + odd[9]
even[9] = odd[9] + odd[6] + odd[8]
else:
odd[0] = even[0] + even[8]
odd[1] = even[1] + even[2] + even[4]
odd[2] = even[2] + even[1] + even[3] + even[5]
odd[3] = even[3] + even[2] + even[6]
odd[4] = even[4] + even[1] + even[5] + even[7]
odd[5] = even[5] + even[2] + even[4] + even[8] + even[6]
odd[6] = even[6] + even[3] + even[5] + even[9]
odd[7] = even[7] + even[4] + even[8]
odd[8] = even[8] + even[0] + even[5] + even[7] + even[9]
odd[9] = even[9] + even[6] + even[8]
# Get count of all possible numbers of length "n" starting
# with digit 0, 1, 2, ..., 9
totalCount = 0
if(useOdd == 1):
for i in range(10):
totalCount += even[i]
else:
for i in range(10):
totalCount += odd[i]
return totalCount
# Driver program to test above function
if __name__ == "__main__":
keypad = [['1','2','3'],
['4','5','6'],
['7','8','9'],
['*','0','#']]
print("Count for numbers of length ",1,": ", getCount(keypad, 1))
print("Count for numbers of length ",2,": ", getCount(keypad, 2))
print("Count for numbers of length ",3,": ", getCount(keypad, 3))
print("Count for numbers of length ",4,": ", getCount(keypad, 4))
print("Count for numbers of length ",5,": ", getCount(keypad, 5))
# This code is contributed by
# ChitraNayal
C#
// A Space Optimized C# program to
// count number of possible numbers
// of given length
using System;
class GFG
{
// Return count of all possible numbers of
// length n in a given numeric keyboard
static int getCount(char [,]keypad, int n)
{
if(keypad == null || n <= 0)
return 0;
if(n == 1)
return 10;
// odd[i], even[i] arrays represent count of
// numbers starting with digit i for any length j
int []odd = new int[10];
int []even = new int[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1; // for j = 1
// Bottom Up calculation from j = 2 to n
for (j = 2; j <= n; j++)
{
useOdd = 1 - useOdd;
// Here we are explicitly writing lines
// for each number 0 to 9. But it can always be
// written as DFS on 4X3 grid using row,
// column array valid moves
if(useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] +
odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] +
odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] +
odd[8] + odd[6];
even[6] = odd[6] + odd[3] +
odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] +
odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] +
even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] +
even[8] + even[6];
odd[6] = even[6] + even[3] +
even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] +
even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
// Get count of all possible numbers of
// length "n" starting with digit 0, 1, 2, ..., 9
totalCount = 0;
if(useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
// Driver Code
public static void Main(String[] args)
{
char [,]keypad = {{'1','2','3'},
{'4','5','6'},
{'7','8','9'},
{'*','0','#'}};
Console.Write("Count for numbers of length {0}: {1}\n", 1,
getCount(keypad, 1));
Console.Write("Count for numbers of length {0}: {1}\n", 2,
getCount(keypad, 2));
Console.Write("Count for numbers of length {0}: {1}\n", 3,
getCount(keypad, 3));
Console.Write("Count for numbers of length {0}: {1}\n", 4,
getCount(keypad, 4));
Console.Write("Count for numbers of length {0}: {1}\n", 5,
getCount(keypad, 5));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// A Space Optimized javascript program to
// count number of possible numbers
// of given length
// Return count of all possible numbers of
// length n in a given numeric keyboard
function getCount(keypad , n)
{
if(keypad == null || n <= 0)
return 0;
if(n == 1)
return 10;
// odd[i], even[i] arrays represent count of
// numbers starting with digit i for any length j
var odd = Array.from({length: 10}, (_, i) => 0);
var even = Array.from({length: 10}, (_, i) => 0);
var i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1; // for j = 1
// Bottom Up calculation from j = 2 to n
for (j = 2; j <= n; j++)
{
useOdd = 1 - useOdd;
// Here we are explicitly writing lines
// for each number 0 to 9. But it can always be
// written as DFS on 4X3 grid using row,
// column array valid moves
if(useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] +
odd[3] + odd[5];
even[3] = odd[3] + odd[2] + odd[6];
even[4] = odd[4] + odd[1] +
odd[5] + odd[7];
even[5] = odd[5] + odd[2] + odd[4] +
odd[8] + odd[6];
even[6] = odd[6] + odd[3] +
odd[5] + odd[9];
even[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[5] +
odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[8];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + even[5];
odd[3] = even[3] + even[2] + even[6];
odd[4] = even[4] + even[1] +
even[5] + even[7];
odd[5] = even[5] + even[2] + even[4] +
even[8] + even[6];
odd[6] = even[6] + even[3] +
even[5] + even[9];
odd[7] = even[7] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] +
even[7] + even[9];
odd[9] = even[9] + even[6] + even[8];
}
}
// Get count of all possible numbers of
// length "n" starting with digit 0, 1, 2, ..., 9
totalCount = 0;
if(useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
// Driver Code
var keypad = [['1','2','3'],
['4','5','6'],
['7','8','9'],
['*','0','#']];
document.write("Count for numbers of length "+ 1+": "+
getCount(keypad, 1));
document.write("<br>Count for numbers of length "+ 2+": "+
getCount(keypad, 2));
document.write("<br>Count for numbers of length "+ 3+": "+
getCount(keypad, 3));
document.write("<br>Count for numbers of length "+ 4+": "+
getCount(keypad, 4));
document.write("<br>Count for numbers of length "+ 5+": "+
getCount(keypad, 5));
// This code is contributed by 29AjayKumar
</script>
Count for numbers of length 1: 10 Count for numbers of length 2: 36 Count for numbers of length 3: 138 Count for numbers of length 4: 532 Count for numbers of length 5: 2062
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA