Algoritmo de valla de pintura

Posted on by Rudeus Greyrat

Dada una valla con n postes yk colores, averigüe el número de formas de pintar la valla tal que como máximo 2 postes adyacentes tengan el mismo color. Como la respuesta puede ser grande, devuélvela módulo 10^9 + 7.
Ejemplos:

Entrada: n = 2 k = 4
Salida: 16
Explicación: Tenemos 4 colores y 2 postes.
Formas en que ambas publicaciones tienen el mismo color: 4 
Formas en que ambas publicaciones tienen un color diferente: 4 (opciones para la 1.ª publicación) * 3 (opciones para la 2.ª publicación) = 12

Entrada: n = 3 k = 2
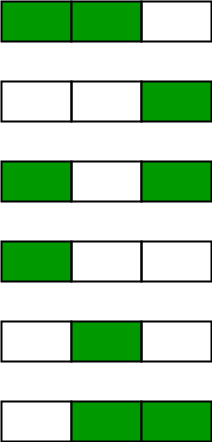
Salida: 6

La siguiente imagen muestra las 6 formas posibles de pintar 3 postes con 2 colores:

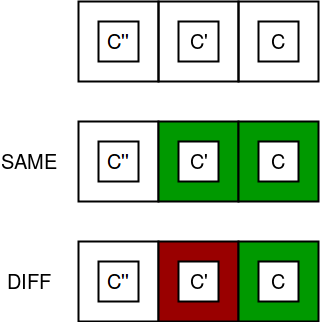
Considere la siguiente imagen en la que c, c’ y c” son los colores respectivos de las publicaciones i, i-1 e i-2.

De acuerdo con la restricción del problema, c = c’ = c” no es posible simultáneamente, así que c’ != c o c” != c o ambos. Hay k – 1 posibilidades para c’ != c y k – 1 para c” != c.

 diff = no of ways when color of last
        two posts is different
 same = no of ways when color of last 
        two posts is same
 total ways = diff + same

for n = 1
    diff = k, same = 0
    total = k

for n = 2
    diff = k * (k-1) //k choices for
           first post, k-1 for next
    same = k //k choices for common 
           color of two posts
    total = k +  k * (k-1)

for n = 3
    diff = k * (k-1)* (k-1) 
           //(k-1) choices for the first place 
        // k choices for the second place
        //(k-1) choices for the third place
    same = k * (k-1) * 2
        // 2 is multiplied because consider two color R and B
        // R R B or B R R 
        // B B R or R B B  
           c'' != c, (k-1) choices for it

Hence we deduce that,
total[i] = same[i] + diff[i]
same[i]  = diff[i-1]
diff[i]  = (diff[i-1] + diff[i-2]) * (k-1)
         = total[i-1] * (k-1)

A continuación se muestra la implementación del problema:

C++

// C++ program for Painting Fence Algorithm
// optimised version
 
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of ways to color k posts
long countWays(int n, int k)
{
    long dp[n + 1];
    memset(dp, 0, sizeof(dp));
    long long mod = 1000000007;
 
    dp[1] = k;
    dp[2] = k * k;
 
    for (int i = 3; i <= n; i++) {
        dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod;
    }
 
    return dp[n];
}
 
// Driver code
int main()
{
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

Java

// Java program for Painting Fence Algorithm
import java.util.*;
 
class GfG {
 
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // To store results for subproblems
        long dp[] = new long[n + 1];
        Arrays.fill(dp, 0);
        int mod = 1000000007;
 
        // There are k ways to color first post
        dp[1] = k;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        int same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = (int)(dp[i - 1] * (k - 1));
            diff = diff % mod;
 
            // Total choices till i.
            dp[i] = (same + diff) % mod;
        }
 
        return dp[n];
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}
 
// This code contributed by Rajput-Ji

Python3

# Python3 program for Painting Fence Algorithm
# optimised version
 
# Returns count of ways to color k posts
def countWays(n, k):
     
    dp = [0] * (n + 1)
    total = k
    mod = 1000000007
     
    dp[1] = k
    dp[2] = k * k   
     
    for i in range(3,n+1):
        dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod
         
    return dp[n]
   
# Driver code
n = 3
k = 2
print(countWays(n, k))
  
# This code is contributed by shubhamsingh10

C#

// C# program for Painting Fence Algorithm
using System;
public class GFG
{
 
  // Returns count of ways to color k posts
  // using k colors
  static long countWays(int n, int k)
  {
 
    // To store results for subproblems
    long[] dp = new long[n + 1];
    Array.Fill(dp, 0);
    int mod = 1000000007;
 
    // There are k ways to color first post
    dp[1] = k;
 
    // There are 0 ways for single post to
    // violate (same color_ and k ways to
    // not violate (different color)
    int same = 0, diff = k;
 
    // Fill for 2 posts onwards
    for (int i = 2; i <= n; i++)
    {
 
      // Current same is same as previous diff
      same = diff;
 
      // We always have k-1 choices for next post
      diff = (int)(dp[i - 1] * (k - 1));
      diff = diff % mod;
 
      // Total choices till i.
      dp[i] = (same + diff) % mod;
    }
 
    return dp[n];
  }
 
  // Driver code
  static public void Main()
  {
    int n = 3, k = 2;
    Console.WriteLine(countWays(n, k));
  }
}
 
// This code is contributed by avanitrachhadiya2155

JavaScript

<script>
    // Javascript program for Painting Fence Algorithm
     
    // Returns count of ways to color k posts
    // using k colors
    function countWays(n, k)
    {
 
      // To store results for subproblems
      let dp = new Array(n + 1);
      dp.fill(0);
      let mod = 1000000007;
 
      // There are k ways to color first post
      dp[1] = k;
 
      // There are 0 ways for single post to
      // violate (same color_ and k ways to
      // not violate (different color)
      let same = 0, diff = k;
 
      // Fill for 2 posts onwards
      for (let i = 2; i <= n; i++)
      {
 
        // Current same is same as previous diff
        same = diff;
 
        // We always have k-1 choices for next post
        diff = (dp[i - 1] * (k - 1));
        diff = diff % mod;
 
        // Total choices till i.
        dp[i] = (same + diff) % mod;
      }
 
      return dp[n];
    }
     
    let n = 3, k = 2;
    document.write(countWays(n, k));
     
    // This code is contributed by divyeshrabadiya07.
</script>
Producción

6

Optimización del espacio: 
podemos optimizar la solución anterior para usar una variable en lugar de una tabla.
A continuación se muestra la implementación del problema:

C++

// C++ program for Painting Fence Algorithm
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of ways to color k posts
// using k colors
long countWays(int n, int k)
{
    // There are k ways to color first post
    long total = k;
    int mod = 1000000007;
 
    // There are 0 ways for single post to
    // violate (same color) and k ways to
    // not violate (different color)
    int same = 0, diff = k;
 
    // Fill for 2 posts onwards
    for (int i = 2; i <= n; i++) {
        // Current same is same as previous diff
        same = diff;
 
        // We always have k-1 choices for next post
        diff = total * (k - 1);
        diff = diff % mod;
 
        // Total choices till i.
        total = (same + diff) % mod;
    }
 
    return total;
}
 
// Driver code
int main()
{
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

Java

// Java program for Painting Fence Algorithm
class GFG {
 
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // There are k ways to color first post
        long total = k;
        int mod = 1000000007;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        int same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = (int)total * (k - 1);
            diff = diff % mod;
 
            // Total choices till i.
            total = (same + diff) % mod;
        }
        return total;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}
 
// This code is contributed by Mukul Singh

Python3

# Python3 program for Painting
# Fence Algorithm
 
# Returns count of ways to color
# k posts using k colors
def countWays(n, k) :
 
    # There are k ways to color first post
    total = k
    mod = 1000000007
 
    # There are 0 ways for single post to
    # violate (same color_ and k ways to
    # not violate (different color)
    same, diff = 0, k
 
    # Fill for 2 posts onwards
    for i in range(2, n + 1) :
         
        # Current same is same as
        # previous diff
        same = diff
 
        # We always have k-1 choices
        # for next post
        diff = total * (k - 1)
        diff = diff % mod
 
        # Total choices till i.
        total = (same + diff) % mod
     
    return total
 
# Driver code
if __name__ == "__main__" :
 
    n, k = 3, 2
    print(countWays(n, k))
 
# This code is contributed by Ryuga

C#

// C# program for Painting Fence Algorithm
using System;
 
class GFG {
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // There are k ways to color first post
        long total = k;
        int mod = 1000000007;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        long same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = total * (k - 1);
            diff = diff % mod;
 
            // Total choices till i.
            total = (same + diff) % mod;
        }
 
        return total;
    }
 
    // Driver code
    static void Main()
    {
        int n = 3, k = 2;
        Console.Write(countWays(n, k));
    }
}
 
// This code is contributed by DrRoot_

PHP

<?php
// PHP program for Painting Fence Algorithm
 
// Returns count of ways to color k
// posts using k colors
function countWays($n, $k)
{
    // There are k ways to color first post
    $total = $k;
    $mod = 1000000007;
 
    // There are 0 ways for single post to
    // violate (same color_ and k ways to
    // not violate (different color)
    $same = 0;
    $diff = $k;
 
    // Fill for 2 posts onwards
    for ($i = 2; $i <= $n; $i++)
    {
        // Current same is same as previous diff
        $same = $diff;
 
        // We always have k-1 choices for next post
        $diff = $total * ($k - 1);
        $diff = $diff % $mod;
 
        // Total choices till i.
        $total = ($same + $diff) % $mod;
    }
 
    return $total;
}
 
// Driver code
$n = 3;
$k = 2;
echo countWays($n, $k) . "\n";
 
// This code is contributed by ita_c
?>

JavaScript

<script>
 
    // JavaScript program for Painting Fence Algorithm
     
    // Returns count of ways to color k posts
    // using k colors
    function countWays(n, k)
    {
        // There are k ways to color first post
        let total = k;
        let mod = 1000000007;
  
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        let same = 0, diff = k;
  
        // Fill for 2 posts onwards
        for (let i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
  
            // We always have k-1 choices for next post
            diff = total * (k - 1);
            diff = diff % mod;
  
            // Total choices till i.
            total = (same + diff) % mod;
        }
  
        return total;
    }
     
    let n = 3, k = 2;
      document.write(countWays(n, k));
         
</script>
Producción

6
 

Este artículo es una contribución de Aditi Sharma . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *