Campo eléctrico debido a un alambre recto infinitamente largo

La ley de Gauss es una parte muy importante del electromagnetismo y la física. Se utiliza para relacionar la distribución de carga con el campo eléctrico resultante debido a la carga. Esta ley fue formulada por Joseph Lagrange en 1773, seguida por Carl Gauss en 1813. Ambos formularon esta ley en el contexto de la atracción de elipsoides. Esta ley también está incluida en una de las cuatro ecuaciones de Maxwell que forman la base de la electrodinámica clásica. Estudiemos este concepto en detalle.

Ley de Gauss

El flujo eléctrico a través de un área se define como el producto del campo eléctrico con el área de la superficie proyectada perpendicularmente al campo eléctrico. En general, para la ley de Gauss se suponen superficies cerradas. Esta ley es una herramienta importante ya que permite estimar la carga eléctrica encerrada dentro de una superficie cerrada. Esta ley se puede utilizar para simplificar el cálculo de las geometrías que tienen simetría entre ellas.

Flujo eléctrico

Considere una superficie dS y un líquido que fluye a lo largo de la superficie con una velocidad «v». La tasa de flujo de líquido a través de la superficie viene dada por «vdS». Se dice que este es el flujo del líquido que fluye a través de la superficie. De manera similar, se define el flujo del campo eléctrico. Se define como el campo eléctrico que fluye a través de un parche de área pequeña “dS”. El número de líneas de campo eléctrico que atraviesan el parche es proporcional a,

$E.\Delta S$

Si el área está inclinada por un ángulo

$E\Delta S cos(\theta)$

El flujo se denota por $\phi$ ,

$\phi = E\Delta S cos(\theta)$

Ley de Gauss

Considere una pequeña carga «q» mantenida dentro de una esfera de radio r. Esta esfera se puede dividir en elementos de área más pequeños como se muestra en la figura a continuación. El campo eléctrico que pasa a través de ese elemento se dará como,

$\phi = E.\Delta S = \frac{q}{4\pi \epsilon r^2}\hat{r}.\Delta S$

El flujo total se puede calcular sumando el flujo a través de elementos individuales,

$\phi = E.\Delta S = \frac{q}{4\pi \epsilon r^2}\sum_{S} \Delta S$

Ahora, el área total de la esfera será $4\pi r^2$

$\phi = E.\Delta S = \frac{q}{4\pi \epsilon r^2}4 \pi r^2$

⇒ $\phi = E.\Delta S = \frac{q}{\epsilon}$

Este es el resultado general de la ley de Gauss.

El flujo total a lo largo de una superficie cerrada S, que encierra una carga q es,

$\phi = \frac{q}{\epsilon}$

Campo eléctrico debido a un alambre recto infinitamente largo

La ley de Gauss se puede utilizar para derivar las ecuaciones de un campo eléctrico a través de una variedad de formas cargadas. Considere un alambre infinitamente largo que contiene la carga. La carga por unidad de longitud de ese cable viene dada por $\lambda$ . El alambre tiene un eje de simetría que se muestra en la siguiente figura. El objetivo es derivar la ecuación para calcular el campo eléctrico producido por este cable.

Suponga que se toma un vector radial OP y se gira alrededor del alambre. Esto significa que el campo eléctrico debe tener el mismo valor en todos los puntos P, P’ y P”. La dirección del campo eléctrico es radialmente hacia afuera si la carga es positiva y viceversa.

Para calcular el campo eléctrico, imagine una superficie gaussiana cilíndrica. Como el campo es radial en todas partes, el flujo a lo largo de las dos caras de los cilindros es cero. En la parte cilíndrica de la superficie, E es perpendicular a la superficie en cada punto y su magnitud es constante ya que depende únicamente de r. El área de superficie de la parte curva es $2\pi rl$ donde l es la longitud del cilindro.

Flujo a través de la superficie = flujo a través de la parte curva del cilindro

= E x $2\pi rl$

La superficie encierra una carga igual a $\lambda l$

$E \times 2\pi r l = \frac{\lambda l}{\epsilon} \\ = E = \frac{\lambda}{2\pi r \epsilon}$

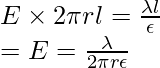
Veamos algunos ejemplos de problemas.

Problemas de muestra

Pregunta 1: En la ley de Gauss, la carga puntual dentro de la superficie cerrada debe estar distribuida en,

secuencialmente
Racional
En línea
Arbitrario.

Responder:

De acuerdo con la ley de Gauss, el flujo que sale del caparazón encerrado solo depende de la cantidad de carga encerrada dentro del caparazón.

Se puede distribuir arbitrariamente.

Por lo tanto, responde (4).

Pregunta 2: El flujo que atraviesa un prisma hexagonal es de 2 x 10 ³ Nm ² /C. ¿Cuál es la carga dentro del prisma hexagonal?

Responder:

De acuerdo con la ley de Gauss, el flujo y las cargas están relacionados por la siguiente ecuación:

$\phi = \frac{q}{\epsilon}$

Dado: ∅ = 2 x 10 ³ Nm ² /C

reemplazando este valor en la ecuación,

$\phi = \frac{q}{\epsilon}$

⇒ $2 \times 10^3 = \frac{q}{\epsilon}$

⇒ $2 \times 10^3 = \frac{q}{8.85 \times 10^{-12}}$

⇒ q = 1.77 × 10 ^-8C

Pregunta 3: El flujo que ingresa a una superficie en forma de cubo es 1 x 10 ³ Nm ² /C y el flujo que sale es 4 x 10 ³ N.m ² /C. ¿Cuál es la carga dentro del prisma hexagonal?

Responder:

De acuerdo con la ley de Gauss, el flujo y las cargas están relacionados por la siguiente ecuación:

$\phi = \frac{q}{\epsilon}$

Dado: ∅ _entrada = 4 x 10 ³ Nm ² /C y ∅ _salida = 1 x 10 ³ Nm ² /C

∅ _neto =∅ _{fuera –} ∅ _entrada = 3 x 10 ³ Nm ² /C

reemplazando este valor en la ecuación,

$\phi = \frac{q}{\epsilon}$

⇒ $3 \times 10^3 = \frac{q}{\epsilon}$

⇒ $3 \times 10^3 = \frac{q}{8.85 \times 10^{-12}}$

⇒ q = 2.665 × 10 ^-8C

Pregunta 4: Encuentre el campo eléctrico a 5 m de un cable infinitamente largo con una densidad de carga lineal de 5 x 10 ^-3 C/m.

Responder:

El campo eléctrico debido a un conductor de carga infinita viene dado por,

$E = \frac{\lambda}{2\pi r \epsilon}$

Dado: r = 5m y $\lambda = 5 \times 10^{-3}$

reemplazando los valores en la ecuación,

$E = \frac{\lambda}{2\pi r \epsilon}$

⇒ $E = \frac{5 \times 10^{-3}}{2\pi (5)(8.85 \times 10^{-12})}$

⇒ E = 18 × 10 ⁹ × 10 ^-3

⇒ mi = 18 × 10 ⁶

Pregunta 5: Encuentre el campo eléctrico a 1 m de un cable infinitamente largo con una densidad de carga lineal de 2 x 10 ^-3 C/m.

Responder:

El campo eléctrico debido a un conductor de carga infinita viene dado por,

$E = \frac{\lambda}{2\pi r \epsilon}$

Dado: r = 1m y $\lambda = 2 \times 10^{-3}$

reemplazando los valores en la ecuación,

$E = \frac{\lambda}{2\pi r \epsilon}$

⇒ $E = \frac{2 \times 10^{-3}}{2\pi (5)(8.85 \times 10^{-12})}$

⇒ E = 18 x 10 ⁹ x 2 x 10 ^-3

⇒ E = 36 x 10 ⁶ N/C

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ley de Gauss

Campo eléctrico debido a un alambre recto infinitamente largo

Problemas de muestra

Deja una respuesta Cancelar la respuesta