Introducción del árbol B+

Para implementar la indexación multinivel dinámica, B-treey el árbol B+ se emplean generalmente. Sin embargo, el inconveniente del árbol B utilizado para la indexación es que almacena el puntero de datos (un puntero al bloque de archivo de disco que contiene el valor clave), correspondiente a un valor clave particular, junto con ese valor clave en el Node de un árbol B. Esta técnica reduce en gran medida el número de entradas que se pueden empaquetar en un Node de un árbol B, lo que contribuye al aumento del número de niveles en el árbol B y, por lo tanto, aumenta el tiempo de búsqueda de un registro. El árbol B+ elimina el inconveniente anterior al almacenar punteros de datos solo en los Nodes de hoja del árbol. Por tanto, la estructura de los Nodes hoja de un árbol B+ es bastante diferente de la estructura de los Nodes internos del árbol B. Cabe señalar aquí que, dado que los punteros de datos están presentes solo en los Nodes hoja, los Nodes hoja necesariamente deben almacenar todos los valores clave junto con sus correspondientes punteros de datos al bloque de archivos del disco, para poder acceder a ellos. Además, los Nodes hoja están vinculados para proporcionar un acceso ordenado a los registros. Los Nodes hoja, por lo tanto, forman el primer nivel del índice, y los Nodes internos forman los otros niveles de un índice multinivel. Algunos de los valores clave de los Nodes hoja también aparecen en los Nodes internos, para actuar simplemente como un medio para controlar la búsqueda de un registro. De la discusión anterior, es evidente que un árbol B+, a diferencia de un árbol B, tiene dos órdenes, ‘a’ y ‘b’, uno para los Nodes internos y el otro para los Nodes externos (u hojas). Los Nodes hoja, por lo tanto, forman el primer nivel del índice, y los Nodes internos forman los otros niveles de un índice multinivel. Algunos de los valores clave de los Nodes hoja también aparecen en los Nodes internos, para actuar simplemente como un medio para controlar la búsqueda de un registro. De la discusión anterior, es evidente que un árbol B+, a diferencia de un árbol B, tiene dos órdenes, ‘a’ y ‘b’, uno para los Nodes internos y el otro para los Nodes externos (u hojas). Los Nodes hoja, por lo tanto, forman el primer nivel del índice, y los Nodes internos forman los otros niveles de un índice multinivel. Algunos de los valores clave de los Nodes hoja también aparecen en los Nodes internos, para actuar simplemente como un medio para controlar la búsqueda de un registro. De la discusión anterior, es evidente que un árbol B+, a diferencia de un árbol B, tiene dos órdenes, ‘a’ y ‘b’, uno para los Nodes internos y el otro para los Nodes externos (u hoja).La estructura de los Nodes internos de un árbol B+ de orden ‘a’ es la siguiente:

1. Cada Node interno tiene la forma: <P ₁ , K ₁ , P ₂ , K ₂ , ….., P _c-1 , K _c-1 , P _c > donde c <= a y cada P _i es un árbol puntero (es decir, apunta a otro Node del árbol) y, cada K _i es un valor clave (consulte el diagrama-I como referencia).
2. Cada Node interno tiene: K ₁ < K ₂ < …. < K _c-1
3. Para cada valor de campo de búsqueda ‘X’ en el subárbol señalado por P _i , se cumple la siguiente condición: K _i-1 < X <= K _i , para 1 < i < c y, K _i-1 < X, for i = c (Ver diagrama I como referencia)
4. Cada Node interno tiene como máximo punteros de árbol ‘a’.
5. El Node raíz tiene, al menos, dos punteros de árbol, mientras que los otros Nodes internos tienen al menos \ceil(a/2) punteros de árbol cada uno.
6. Si un Node interno tiene punteros ‘c’, c <= a, entonces tiene valores clave ‘c – 1’.

Diagram-I The structure of the leaf nodes of a B+ tree of order ‘b’ is as follows:

1. Cada Node hoja tiene la forma: <<K ₁ , D ₁ >, <K ₂ , D ₂ >, ….., <K _c-1 , D _c-1 >, P _next > donde c <= b y cada D _i es un puntero de datos (es decir, apunta a un registro real en el disco cuyo valor clave es K _i o a un bloque de archivo de disco que contiene ese registro) y, cada K _i es un valor clave y, P _next , apunta al siguiente Node hoja en el árbol B+ (ver diagrama II como referencia).
2. Cada Node hoja tiene: K ₁ < K ₂ < …. < K _c-1 , c <= segundo
3. Cada Node hoja tiene al menos valores de \ceil(b/2).
4. Todos los Nodes hoja están al mismo nivel.

Diagram-II Using the P_next pointer it is viable to traverse all the leaf nodes, just like a linked list, thereby achieving ordered access to the records stored in the disk. A Diagram of B+ Tree – 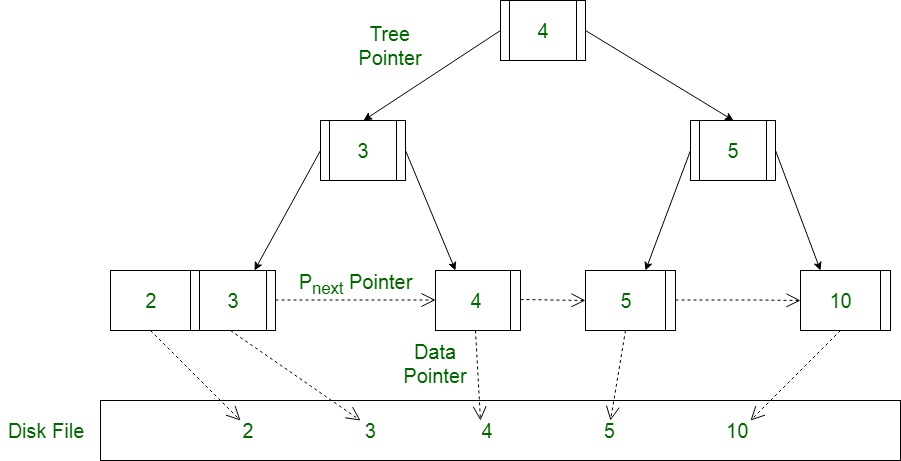Advantage – A B+ tree with ‘l’ levels can store more entries in its internal nodes compared to a B-tree having the same ‘l’ levels. This accentuates the significant improvement made to the search time for any given key. Having lesser levels and the presence of P_next pointers imply that the B+ trees is very quick and efficient in accessing records from disks.

Aplicación de árboles B+:

• Indexación multinivel
• Operaciones más rápidas en el árbol (inserción, eliminación, búsqueda)
• Indexación de bases de datos