Rompecabezas | Torneo de eliminación simple

En un torneo de eliminación simple, como los campeonatos de Grand Slam de tenis, todos los jugadores perdedores son eliminados inmediatamente de las rondas posteriores hasta que se determina un solo jugador. Si hay N jugadores al comienzo del torneo, responda las siguientes preguntas.

1. ¿Cuál es el número total de partidos necesarios para obtener un ganador?
2. ¿Cuántas rondas hay en un torneo así?
3. ¿Cuántos partidos más se necesitan jugar para determinar el segundo mejor jugador con base en la información producida por el torneo?

Solución

1. Ya que estamos eliminando a un jugador en cada partida, y solo hay un ganador. Entonces, en total se necesitan jugadores N-1 para ser eliminados. Por lo tanto, se necesitan coincidencias N-1 para obtener un ganador. Matemáticamente, si hay N jugadores, entonces tendremos N/2 partidos en la primera ronda, N/4 partidos en la segunda ronda, y así sucesivamente hasta que tengamos 1 partido en la ronda final. Entonces, el número total de coincidencias es solo la suma de la progresión geométrica, con términos N/2, N/4 hasta 1 .

   Sea un número total de N jugadores, luego el número total de partidos para obtener un ganador:

   => N/2 + N/4 + N/8 + …. + 2 + 1

   Esta es una progresión geométrica con
   a = N/2, r = 1/2
   El número de términos en la progresión será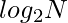

   Por lo tanto,
   => N/2(1 – (1/2)^{log_2N}) / 1 – 1/2)
   => N(1 – 1/2^{log_2N})
   => N(1 – 1/N )
   => (N – 1)

2. El número total de rondas en el torneo es log ₂ N si N es una potencia de 2 , ya que en cada ronda se elimina la mitad de los jugadores, hasta que solo queda un jugador. Si N no es una potencia de 2 , entonces el número de rondas es la potencia más pequeña de 2 , que es mayor o igual que N, que es igual a ceil(log ₂ N) .
3. El segundo mejor jugador puede ser cualquier jugador que haya perdido ante el ganador y nadie más. Se puede hacer que estos jugadores jueguen su propio torneo de eliminación simple. Ya que, el ganador estará presente en todas las rondas del torneo, por lo que en total habrá jugadores ceil(log ₂ N) compitiendo por el segundo mejor jugador. Dado que, para un torneo de N jugadores, se juegan N-1 partidos para averiguar el ganador, por lo tanto, se requieren ceil (log ₂ N) – 1 partidos para determinar el ganador entre los contendientes, que será nuestro segundo mejor jugador.