Diferencia entre STING y OPTICS

El método para identificar grupos de datos similares en un conjunto de datos se denomina agrupación. Las entidades de cada grupo son comparativamente más similares a las entidades de ese grupo que a las de los otros grupos. 

STING (algoritmo de agrupación en cuadrícula de información estadística) y OPTICS (punto de pedido para identificar el algoritmo de agrupación en agrupación de la estructura de agrupación) son algoritmos de agrupación utilizados en el aprendizaje no supervisado. Son técnicas de aprendizaje automático que se utilizan para agrupar los puntos de datos de entrada dados en grupos o grupos en función de sus atributos. STING es un algoritmo de agrupamiento basado en cuadrículas, mientras que OPTICS es un algoritmo de agrupamiento basado en densidad. Agrupación 

Estas son algunas diferencias entre STING y OPTICS .  

S. No.	PICADURA	ÓPTICA
1.	STING es la abreviatura de Red de información estadística	OPTICS es la abreviatura de Punto de pedido para identificar la estructura de agrupamiento
2.	Es un algoritmo de agrupamiento basado en grib	Es un algoritmo de agrupamiento basado en la densidad.
3.	No se trata de puntos de datos sino del espacio de valores que rodea los puntos de datos.	Busca en el espacio de datos áreas de puntos de datos de densidad variada en el espacio de datos.
4.	Utiliza una estructura de datos de cuadrícula multidimensional que cuantifica el espacio en un número finito de celdas.	Es una extensión del agrupamiento espacial basado en la densidad de aplicaciones con ruido.
5.	Las siguientes son las propiedades del algoritmo de agrupamiento STING:  El área espacial se divide en celdas rectangulares. Varios niveles de celdas a diferentes niveles de resolución. La celda de alto nivel se divide en varias celdas de bajo nivel. Los atributos estadísticos se almacenan en la celda, por ejemplo, Media, Máximo, Mínimo son algunas de las medidas estadísticas que se utilizan. La información estadística se calcula para cada celda y los tipos de distribución calculados son normal y exponencial.	Las siguientes son las propiedades del algoritmo de agrupamiento OPTICS:  Es una extensión de DBSCAN, que asume la responsabilidad de los parámetros que pueden conducir al descubrimiento de clústeres inaceptables. La distancia del núcleo es el punto más pequeño que hace un punto central. Se requieren dos parámetros importantes para OPTICS: épsilon («eps) y puntos mínimos («MinPts). El parámetro eps define la distancia de vecindad alrededor de un punto P. El parámetro MinPts es el número mínimo. de vecinos dentro del radio “eps”. Densidad = No. de puntos dentro de un radio especificado r(eps)
6.	Tiene una complejidad computacional relativamente menor.	Tiene relativamente más complejidad computacional.

Algoritmo STING:  

1. Determinar una capa, para empezar.
2. Para cada celda de esta capa, calculamos el intervalo de confianza (o rango estimado) de probabilidad de que esta celda sea relevante para la consulta.
3. A partir del cálculo del intervalo anterior, etiquetamos la celda como relevante o no relevante.
4. Si esta es la capa inferior, termine el proceso.
5. Bajamos un nivel en la estructura jerárquica. Vaya al Paso 2 para aquellos niveles que forman las celdas relevantes de la capa de nivel superior.

Diagrama de jerarquía de STING: 
 

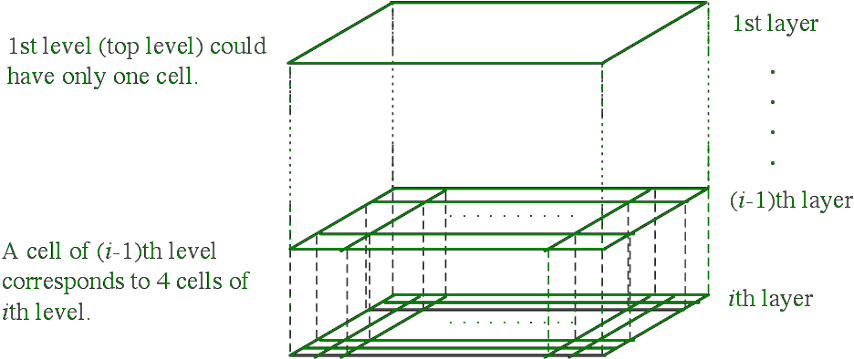
Algoritmo ÓPTICO: 
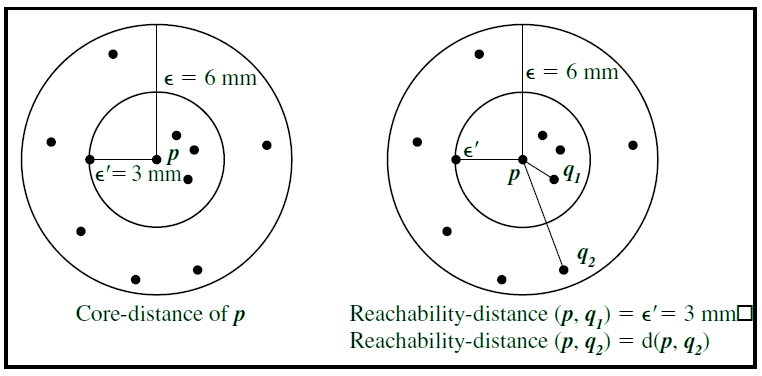
La distancia al núcleo de un punto P es la distancia más pequeña tal que la vecindad de P tenga al menos minPts puntos. 
La distancia de accesibilidad de p desde q1 es la distancia del núcleo ( ε’ ). 
La distancia de accesibilidad de p desde q2 es la distancia euclidiana entre p y q2.