Número mínimo de operaciones dadas requeridas para convertir una permutación en una permutación de identidad

Dada una permutación P (P1, P2, P3, … Pn) de los primeros n números naturales. Encuentre el número mínimo de operaciones para convertirlo en una permutación de identidad, es decir , 1, 2, 3, …, n donde cada operación se define como: 
P[i] = P[P[P[i]]]  i de 1 a n (1 indexación basada). Si no hay forma de convertir, imprima -1 .
Ejemplos: 
 

Entrada: arr[] = {2, 3, 1} 
Salida: 1 
Después de 1 operación: 
P[1] = P[P[P[1]]] = P[P[2]] = P[3] = 1 
P[2] = P[P[P[2]]] = P[P[3]] = P[1] = 2 
P[3] = P[P[P[3]]] = P[P[ 1]] = P[2] = 3 
Así después de 1 operación obtenemos una permutación de identidad.
Entrada: arr[] = {2, 1, 3} 
Salida: -1 
No hay forma de obtener la permutación de identidad 
sin importar cuántas operaciones apliquemos. 
 

Enfoque: Primero, encuentre todos los ciclos en la permutación dada. Aquí, un ciclo es un gráfico dirigido en el que hay una arista desde un elemento e hasta el elemento en la posición e. 
Por ejemplo, aquí está el gráfico de permutación {4, 6, 5, 3, 2, 1, 8, 7} 
 

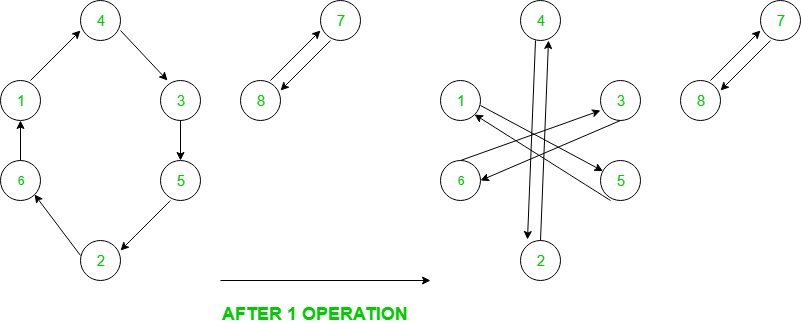
Ahora, en una operación, cada ciclo de longitud 3k se divide en 3 ciclos cada uno de longitud k mientras que los ciclos de longitud 3k+1 o 3k+2 no se dividen. Dado que al final, necesitamos todos los ciclos de longitud 1, por lo tanto, todos los ciclos deben ser una potencia de 3, de lo contrario, la respuesta no existe. La respuesta sería entonces el máximo de log (base 3) de todas las longitudes de ciclo.
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
int calculateCycleOperations(int len)
{
    int cycle_operations = 0;
    while (len) {
        len /= 3;
        ++cycle_operations;
    }
    return --cycle_operations;
}
 
// Function to return the minimum operations required
int minimumOperations(int p[], int n)
{
 
    // Array to keep track of visited elements
    bool visited[n + 1] = { 0 };
 
    // To store the final answer
    int ans = 0;
 
    // Looping through all the elements
    for (int i = 1; i <= n; i++) {
 
        // Current element
        int ele = p[i];
 
        // If current element is not present in the
        // previous cycles then only consider this
        if (!visited[ele]) {
 
            // Mark current element visited so that it
            // will not be considered in other cycles
            visited[ele] = 1;
 
            // To store the length of each cycle
            int len = 1;
            ele = p[ele];
 
            // Calculating cycle length
            while (!visited[ele]) {
                visited[ele] = 1;
                ++len;
                ele = p[ele];
            }
 
            // Operations needed for this cycle to reduce
            // to length 1 (if possible)
            int operations = calculateCycleOperations(len);
 
            // Checking cycle length to be power of 3
            // if not, then return -1
            int num = pow(3, operations);
            if (num != len) {
                return -1;
            }
 
            // Taking maximum of the operations
            ans = max(ans, operations);
        }
    }
    return ans;
}
 
// Driver code
int main()
{
    // 1-based indexing
    int P[] = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
    int n = (sizeof(P) / sizeof(P[0])) - 1;
 
    // Calling function
    cout << minimumOperations(P, n);
 
    return 0;
}

// Java implementation of the approach
import java.util.*;
 
class GFG
{
 
static int calculateCycleOperations(int len)
{
    int cycle_operations = 0;
    while (len > 0)
    {
        len /= 3;
        ++cycle_operations;
    }
    return --cycle_operations;
}
 
// Function to return the minimum operations required
static int minimumOperations(int p[], int n)
{
 
    // Array to keep track of visited elements
    int []visited = new int[n+1];
    Arrays.fill(visited,0);
 
    // To store the final answer
    int ans = 0;
 
    // Looping through all the elements
    for (int i = 1; i <= n; i++)
    {
 
        // Current element
        int ele = p[i];
 
        // If current element is not present in the
        // previous cycles then only consider this
        if (visited[ele] == 0)
        {
 
            // Mark current element visited so that it
            // will not be considered in other cycles
            visited[ele] = 1;
 
            // To store the length of each cycle
            int len = 1;
            ele = p[ele];
 
            // Calculating cycle length
            while (visited[ele] == 0)
            {
                visited[ele] = 1;
                ++len;
                ele = p[ele];
            }
 
            // Operations needed for this cycle to reduce
            // to length 1 (if possible)
            int operations = calculateCycleOperations(len);
 
            // Checking cycle length to be power of 3
            // if not, then return -1
            int num = (int)Math.pow(3, operations);
            if (num != len) {
                return -1;
            }
 
            // Taking maximum of the operations
            ans = Math.max(ans, operations);
        }
    }
    return ans;
}
 
// Driver code
public static void main(String args[])
{
    // 1-based indexing
    int P[] = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
    int n = P.length-1;
 
    // Calling function
    System.out.println(minimumOperations(P, n));
}
}
 
// This code is contributed by
// Surendra_Gangwar

# Python3 implementation of the approach
def calculateCycleOperations(length):
 
    cycle_operations = 0
    while length > 0:
        length //= 3
        cycle_operations += 1
     
    return cycle_operations - 1
 
# Function to return the minimum
# operations required
def minimumOperations(p, n):
 
    # Array to keep track of visited elements
    visited = [0] * (n + 1)
 
    # To store the final answer
    ans = 0
 
    # Looping through all the elements
    for i in range(1, n + 1):
 
        # Current element
        ele = p[i]
 
        # If current element is not present in the
        # previous cycles then only consider this
        if not visited[ele]:
 
            # Mark current element visited so that it
            # will not be considered in other cycles
            visited[ele] = 1
 
            # To store the length of each cycle
            length = 1
            ele = p[ele]
 
            # Calculating cycle length
            while not visited[ele]:
                visited[ele] = 1
                length += 1
                ele = p[ele]
             
            # Operations needed for this cycle to
            # reduce to length 1 (if possible)
            operations = calculateCycleOperations(length)
 
            # Checking cycle length to be power
            # of 3 if not, then return -1
            num = pow(3, operations)
            if num != length:
                return -1
 
            # Taking maximum of the operations
            ans = max(ans, operations)
         
    return ans
 
# Driver code
if __name__ == "__main__":
 
    # 1-based indexing
    P = [-1, 4, 6, 5, 3, 2, 7, 8, 9, 1]
    n = len(P) - 1
 
    # Calling function
    print(minimumOperations(P, n))
 
# This code is contributed by Rituraj Jain

// C# implementation of the above approach
using System;
 
class GFG
{
 
    static int calculateCycleOperations(int len)
    {
        int cycle_operations = 0;
        while (len > 0)
        {
            len /= 3;
            ++cycle_operations;
        }
        return --cycle_operations;
    }
     
    // Function to return the minimum operations required
    static int minimumOperations(int []p, int n)
    {
     
        // Array to keep track of visited elements
        int []visited = new int[n+1];
 
        // To store the final answer
        int ans = 0;
     
        // Looping through all the elements
        for (int i = 1; i <= n; i++)
        {
     
            // Current element
            int ele = p[i];
     
            // If current element is not present in the
            // previous cycles then only consider this
            if (visited[ele] == 0)
            {
     
                // Mark current element visited so that it
                // will not be considered in other cycles
                visited[ele] = 1;
     
                // To store the length of each cycle
                int len = 1;
                ele = p[ele];
     
                // Calculating cycle length
                while (visited[ele] == 0)
                {
                    visited[ele] = 1;
                    ++len;
                    ele = p[ele];
                }
     
                // Operations needed for this cycle to reduce
                // to length 1 (if possible)
                int operations = calculateCycleOperations(len);
     
                // Checking cycle length to be power of 3
                // if not, then return -1
                int num = (int)Math.Pow(3, operations);
                if (num != len)
                {
                    return -1;
                }
     
                // Taking maximum of the operations
                ans = Math.Max(ans, operations);
            }
        }
        return ans;
    }
     
    // Driver code
    public static void Main()
    {
        // 1-based indexing
        int []P = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
        int n = P.Length-1;
     
        // Calling function
        Console.WriteLine(minimumOperations(P, n));
    }
}
 
// This code is contributed by Ryuga

<?php
// PHP implementation of the approach
function calculateCycleOperations($len)
{
    $cycle_operations = 0;
    while ($len)
    {
        $len = (int)($len / 3);
        ++$cycle_operations;
    }
    return --$cycle_operations;
}
 
// Function to return the minimum
// operations required
function minimumOperations($p, $n)
{
 
    // Array to keep track of visited elements
    $visited[$n + 1] = array(0);
 
    // To store the final answer
    $ans = 0;
 
    // Looping through all the elements
    for ($i = 1; $i <= $n; $i++)
    {
 
        // Current element
        $ele = $p[$i];
 
        // If current element is not present in the
        // previous cycles then only consider this
        if (!$visited[$ele])
        {
 
            // Mark current element visited so that it
            // will not be considered in other cycles
            $visited[$ele] = 1;
 
            // To store the length of each cycle
            $len = 1;
            $ele = $p[$ele];
 
            // Calculating cycle length
            while (!$visited[$ele])
            {
                $visited[$ele] = 1;
                ++$len;
                $ele = $p[$ele];
            }
 
            // Operations needed for this cycle to reduce
            // to length 1 (if possible)
            $operations = calculateCycleOperations($len);
 
            // Checking cycle length to be power of 3
            // if not, then return -1
            $num = pow(3, $operations);
            if ($num != $len)
            {
                return -1;
            }
 
            // Taking maximum of the operations
            $ans = max($ans, $operations);
        }
    }
    return $ans;
}
 
// Driver code
 
// 1-based indexing
$P = array(-1, 4, 6, 5, 3, 2, 7, 8, 9, 1);
$n = sizeof($P) - 1;
 
// Calling function
echo minimumOperations($P, $n);
 
// This code is contributed by Akanksha Rai
?>

<script>
 
// JavaScript implementation of the approach
 
function calculateCycleOperations(len)
{
    let cycle_operations = 0;
    while (len > 0)
    {
        len = Math.floor(len / 3);
        ++cycle_operations;
    }
    return --cycle_operations;
}
   
// Function to return the minimum operations required
function minimumOperations(p, n)
{
   
    // Array to keep track of visited elements
    let visited = Array.from({length: n + 1}, (_, i) => 0);
   
    // To store the final answer
    let ans = 0;
   
    // Looping through all the elements
    for (let i = 1; i <= n; i++)
    {
   
        // Current element
        let ele = p[i];
   
        // If current element is not present in the
        // previous cycles then only consider this
        if (visited[ele] == 0)
        {
   
            // Mark current element visited so that it
            // will not be considered in other cycles
            visited[ele] = 1;
   
            // To store the length of each cycle
            let len = 1;
            ele = p[ele];
   
            // Calculating cycle length
            while (visited[ele] == 0)
            {
                visited[ele] = 1;
                ++len;
                ele = p[ele];
            }
   
            // Operations needed for this cycle to reduce
            // to length 1 (if possible)
            let operations = calculateCycleOperations(len);
   
            // Checking cycle length to be power of 3
            // if not, then return -1
            let num = Math.floor(Math.pow(3, operations));
            if (num != len) {
                return -1;
            }
   
            // Taking maximum of the operations
            ans = Math.max(ans, operations);
        }
    }
    return ans;
}
     
    // Driver code
     
    // 1-based indexing
    let P = [ -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 ];
    let n = P.length - 1;
   
    // Calling function
    document.write(minimumOperations(P, n));
                 
</script>

2

Complejidad del tiempo: O(N*LogN)