Operador de gramática y analizador de precedencia en TOC – Part 1

Una gramática que se utiliza para definir operadores matemáticos se denomina gramática de operadores o gramática de precedencia de operadores . Tales gramáticas tienen la restricción de que ninguna producción tiene un lado derecho vacío (producciones nulas) o dos no terminales adyacentes en su lado derecho.

Ejemplos:
este es un ejemplo de gramática de operadores:

E->E+E/E*E/id 

Sin embargo, la gramática dada a continuación no es una gramática de operadores porque dos no terminales son adyacentes entre sí:

S->SAS/a
A->bSb/b 

Sin embargo, podemos convertirlo en una gramática de operadores:

S->SbSbS/SbS/a
A->bSb/b  

Analizador de precedencia de operadores:
un analizador de precedencia de operadores es un analizador ascendente que interpreta una gramática de operadores. Este analizador solo se usa para gramáticas de operadores. Las gramáticas ambiguas no están permitidas en ningún analizador excepto en el analizador de precedencia de operadores.
Existen dos métodos para determinar qué relaciones de precedencia deben existir entre un par de terminales:

1. Utilice la asociatividad convencional y la precedencia del operador.
2. El segundo método para seleccionar las relaciones de precedencia de operadores consiste primero en construir una gramática inequívoca para el lenguaje, una gramática que refleje la asociatividad y la precedencia correctas en sus árboles de análisis sintáctico.

Este analizador se basa en las siguientes tres relaciones de precedencia: ⋖, ≐, ⋗
a ⋖ b Esto significa que a “cede precedencia a” b.
a ⋗ b Esto significa que a “prevalece sobre” b.
a ≐ b Esto significa que a “tiene la misma precedencia que” b.

Figure – Operator precedence relation table for grammar E->E+E/E*E/id

No se proporciona ninguna relación entre id e id, ya que id no se comparará y dos variables no pueden estar una al lado de la otra. También hay una desventaja de esta tabla: si tenemos n operadores, el tamaño de la tabla será n*n y la complejidad será 0(n ² ). Para disminuir el tamaño de la tabla, usamos la tabla de funciones del operador .

Los analizadores de precedencia de operadores normalmente no almacenan la tabla de precedencia con las relaciones; más bien se implementan de una manera especial. Los analizadores de precedencia de operadores utilizan funciones de precedencia que asignan símbolos terminales a números enteros, y las relaciones de precedencia entre los símbolos se implementan mediante comparación numérica. La tabla de análisis se puede codificar mediante dos funciones de precedencia f y g que asignan símbolos de terminal a números enteros. Seleccionamos f y g tales que:

1. f(a) < g(b) siempre que a le dé precedencia a b
2. f(a) = g(b) siempre que a y b tengan la misma precedencia
3. f(a) > g(b) siempre que a prevalece sobre b

Ejemplo: considere la siguiente gramática:

 E -> E + E/E * E/( E )/id   

Este es el gráfico dirigido que representa la función de precedencia:

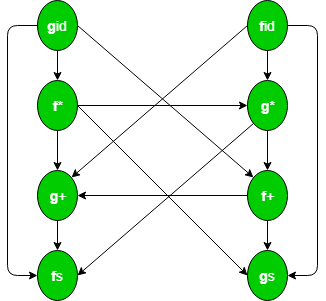
Como no hay ningún ciclo en el gráfico, podemos hacer esta tabla de funciones:

fid -> g* -> f+ ->g+ -> f$
gid -> f* -> g* ->f+ -> g+ ->f$ 

El tamaño de la mesa es 2n .

Una desventaja de las tablas de funciones es que aunque tenemos entradas en blanco en la tabla de relaciones, tenemos entradas que no están en blanco en la tabla de funciones. Las entradas en blanco también se denominan errores. Por lo tanto, la capacidad de detección de errores de la tabla de relaciones es mayor que la de la tabla de funciones.

#include<stdlib.h>
#include<stdio.h>
#include<string.h>
  
// function f to exit from the loop
// if given condition is not true
void f()
{
    printf("Not operator grammar");
    exit(0);
}
  
void main()
{
    char grm[20][20], c;
  
    // Here using flag variable,
    // considering grammar is not operator grammar
    int i, n, j = 2, flag = 0;
  
    // taking number of productions from user
    scanf("%d", &n);
    for (i = 0; i < n; i++)
        scanf("%s", grm[i]);
  
    for (i = 0; i < n; i++) {
        c = grm[i][2];
  
        while (c != '\0') {
  
            if (grm[i][3] == '+' || grm[i][3] == '-'
                || grm[i][3] == '*' || grm[i][3] == '/')
  
                flag = 1;
  
            else {
  
                flag = 0;
                f();
            }
  
            if (c == '$') {
                flag = 0;
                f();
            }
  
            c = grm[i][++j];
        }
    }
  
    if (flag == 1)
        printf("Operator grammar");
}

Input :3
A=A*A
B=AA
A=$

Output : Not operator grammar

Input :2
A=A/A
B=A+A

Output : Operator grammar

$es una producción nula aquí que tampoco está permitida en las gramáticas de operadores.

Ventajas –

1. Se puede construir fácilmente a mano.
2. Es simple implementar este tipo de análisis.

Desventajas –

1. Es difícil manejar tokens como el signo menos (-), que tiene dos precedencias diferentes (dependiendo de si es unario o binario).
2. Es aplicable sólo a una pequeña clase de gramáticas.