Algoritmos de asignación de registros en el diseño del compilador

La asignación de registros es un método importante en la fase final del compilador. Los registros son más rápidos de acceder que la memoria caché. Los registros están disponibles en tamaño pequeño hasta unos pocos cientos de Kb. Por lo tanto, es necesario utilizar un número mínimo de registros para la asignación de variables. Hay tres algoritmos populares de asignación de registros.

1. Asignación de registros ingenuos
2. Algoritmo de exploración lineal
3. Algoritmo de Chaitin

Estos se explican a continuación a continuación.

1. Asignación de registros ingenuos:

• La asignación ingenua (no) de registros se basa en la suposición de que las variables se almacenan en la memoria principal.
• No podemos realizar operaciones directamente en las variables almacenadas en la memoria principal.
• Las variables se mueven a registros, lo que permite realizar varias operaciones utilizando ALU.
• ALU contiene un registro temporal donde las variables se mueven antes de realizar operaciones aritméticas y lógicas.
• Una vez que se completan las operaciones, necesitamos almacenar el resultado en la memoria principal en este método.
• La transferencia de variables desde y hacia la memoria principal reduce la velocidad general de ejecución.

a = b + c
d = a
c = a + d

Variables almacenadas en la memoria principal:

a	b	C	d
2 fps	4 fps	6 fps	8 fps

Instrucciones de nivel de máquina:

LOAD  R1, _4fp
LOAD  R2, _6fp
ADD   R1, R2 
STORE R1, _2fp
LOAD  R1, _2fp
STORE R1, _8fp
LOAD  R1, _2fp
LOAD  R2, _8fp
ADD   R1, R2
STORE R1, _6fp

ventajas :

• Operaciones fáciles de entender y el flujo de variables desde la memoria principal a los registros y viceversa.
• Solo 2 registros son suficientes para realizar cualquier operación.
• La complejidad del diseño es menor.

Desventajas:

• La complejidad del tiempo aumenta a medida que las variables se mueven a registros desde la memoria principal.
• Demasiadas instrucciones LOAD y STORE.
• Para acceder a una variable por segunda vez, necesitamos ALMACENARLA en la memoria principal para registrar cualquier cambio realizado y CARGARLA nuevamente.
• Este método no es adecuado para los compiladores modernos.

2. Algoritmo de exploración lineal:

• El algoritmo de exploración lineal es un mecanismo de asignación de registro global.
• Es un enfoque de abajo hacia arriba.
• Si n variables están activas en cualquier momento, entonces necesitamos ‘n’ registros.
• En este algoritmo, las variables se escanean linealmente para determinar los rangos activos de la variable en función de los cuales se asignan los registros.
• La idea principal detrás de este algoritmo es que asignar un número mínimo de registros de modo que estos registros puedan usarse nuevamente y esto depende totalmente del rango en vivo de las variables.
• Para este algoritmo, necesitamos implementar un análisis de variables en vivo de Code Optimization.

a = b + c
d = e + f
d = d + e
IFZ a goto L0
b = a + d
goto L1
L0 : b = a - d 
L1 : i = b

Gráfico de flujo de control:

   

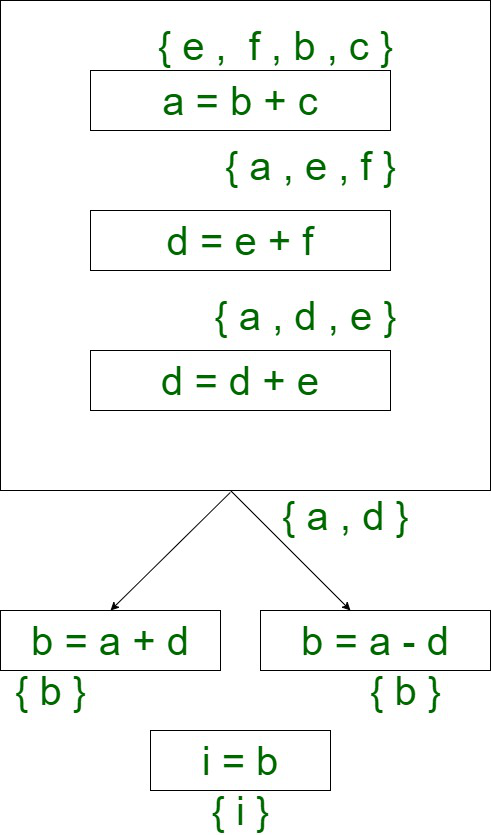
• En cualquier momento, el número máximo de variables activas es 4 en este ejemplo. Por lo tanto, requerimos 4 registros como máximo para la asignación de registros.

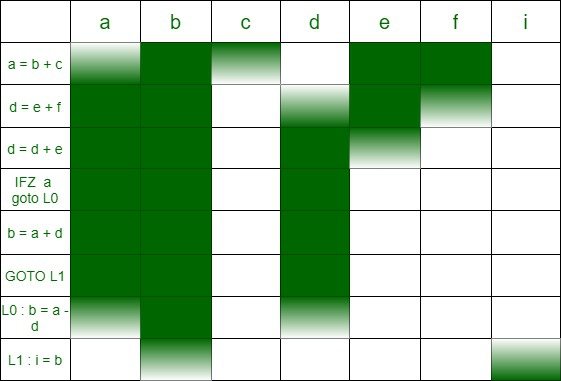
Si dibujamos una línea horizontal en cualquier punto del diagrama anterior, podemos ver que necesitamos exactamente 4 registros para realizar las operaciones en el programa.

Dividir:

• A veces, el número requerido de registros puede no estar disponible. En tal caso, es posible que necesitemos mover algunas variables hacia y desde la RAM. Esto se conoce como derramamiento.
• El derrame se puede hacer de manera efectiva moviendo la variable que se usa menos veces en el programa.

Desventajas:

• El algoritmo de exploración lineal no tiene en cuenta los «agujeros de por vida» de la variable.
• Las variables no están activas en todo el programa y este algoritmo no registra los huecos en el rango activo de la variable.

3. Coloración de gráficos (algoritmo de Chaitin):

• La asignación de registros se interpreta como un problema de coloración de gráficos.
• Los Nodes representan el rango en vivo de la variable.
• Los bordes representan la conexión entre dos rangos vivos.
• Asignar color a los Nodes de manera que no haya dos Nodes adyacentes que tengan el mismo color.
• El número de colores representa el número mínimo de registros necesarios.

Una k coloración del gráfico se asigna a k registros.

Pasos :

1. Elija un Node arbitrario de grado menor que k.
2. Empuje ese Node en la pila y elimine todos sus bordes salientes.
3. Compruebe si los bordes restantes tienen un grado menor que k, si es SÍ, vaya a 5, de lo contrario, vaya a #
4. Si el grado de cualquier vértice restante es menor que k entonces empújelo a la pila.
5. Si no hay más bordes disponibles para empujar y si todos los bordes están presentes en la pila, POP cada Node y coloréelos de manera que no haya dos Nodes adyacentes que tengan el mismo color.
6. El número de colores asignados a los Nodes es el número mínimo de registros necesarios.

# derrame algunos Nodes en función de sus rangos en vivo y luego vuelva a intentarlo con el mismo valor de k. Si el problema persiste, significa que el valor de k asumido no puede ser el número mínimo de registros. Intente aumentar el valor de k en 1 y vuelva a intentar todo el procedimiento.

Para las mismas instrucciones mencionadas anteriormente, el color del gráfico será el siguiente:

Asumiendo k=4 

Después de realizar la coloración del gráfico, el gráfico final se obtiene de la siguiente manera 

Nota: cualquier color (registro) se puede asignar a ‘i’ ya que no tiene borde con ningún otro Node.