Ordena los números dados para formar el número mayor | conjunto 2

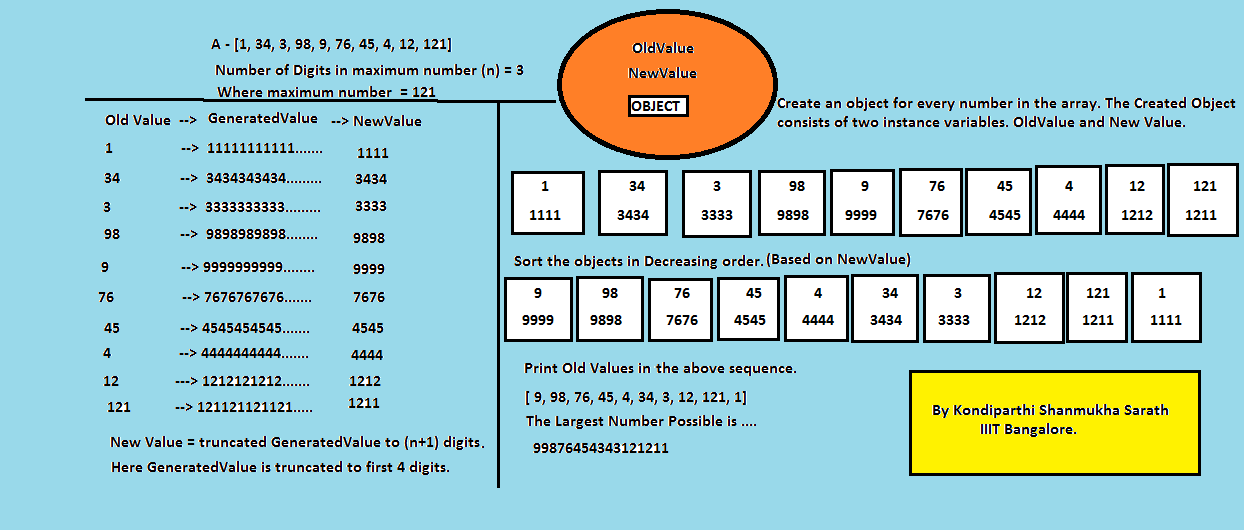
Dada una array de números no negativos (del rango de enteros), es necesario organizarlos en algún orden de modo que proporcione el número máximo. Por ejemplo, la array dada es A[1, 34, 3, 98, 9, 76, 45, 4, 12, 121]. si ordenamos estos números en el siguiente orden, A[9, 98, 76, 45, 4, 34, 3, 12, 121, 1], al unirlos obtenemos “99876454343121211” como el número más grande.

Ejemplos:

Input :  [1, 34, 3, 98, 9, 76, 45, 4, 12, 121]
Output : 99876454343121211

Input :  [12, 121]
Output : 12121

En SET 1 , hemos discutido un enfoque para hacer lo mismo. En este conjunto, discutiremos otra lógica.

1) Encuentra el número de dígitos en el número más grande. Sea n el número de dígitos.
2) Crear una versión extendida de todos los números. En la versión extendida, tenemos n+1 dígitos formados al concatenar el número de consigo mismo y truncar los dígitos extra.
3) Ordenar los números originales según sus valores extendidos.
4) La concatenación de los números ordenados produce el resultado requerido.

// Java program to arrange the numbers to form the
// largest number
import java.math.BigInteger;
import java.util.*;
  
public class LargestNumber
{
    // method that returns largest number form
    public static String largestNumber(List<Integer> arr)
    {
        // finding number of digits in maximum element
        // present in array
        int n =
         Collections.max(arr).toString().length();
  
        ArrayList<ExtendedNum> en =
                       new ArrayList<ExtendedNum>();
        for (int i = 0 ; i < arr.size(); i++)
            en.add(new ExtendedNum(arr.get(i),
                              n));
  
        // sort based on modified value
        Collections.sort(en, (p1, p2) ->
         (int)(p2.modifiedValue - p1.modifiedValue));
  
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < en.size(); i++)
            sb.append(new StringBuilder
            (Long.toString(en.get(i).originalValue)));
  
  
        // To remove any zeroes at head.
        BigInteger bi = new BigInteger(sb.toString());
  
        return bi.toString();
    }
  
    // Driver method
    public static void main(String[] args)
    {
        Integer arr[] = {1, 34, 3, 98, 9, 76, 45,
                                     4, 12, 121};
        List<Integer> l = Arrays.asList(arr);
  
        System.out.println(largestNumber(l));
    }
}
  
// A utility class to generate new value
class ExtendedNum
{
    int originalValue;
    long modifiedValue;
  
    public ExtendedNum(int originalValue, int n)
    {
        this.originalValue = originalValue;
        String s = Integer.toString(originalValue);
        StringBuilder sb = new StringBuilder(s);
        StringBuilder ans = new StringBuilder();
        while (ans.length() <= n + 1)
            ans.append(sb);
  
        s = ans.toString().substring(0, n + 1);
        modifiedValue = Long.parseLong(s);
    }
  
    public String toString()
    {
        return "[" + modifiedValue +
                ", " + originalValue + "]";
    }
}

# Python program to find largest
# number from the given values
# function that return largest
# possible number
def largestNumber(array):
      
    # extval is a empty list for extended 
    # values and ans for calculating answer
    extval, ans = [], ""
      
    # calculating the length of largest number
    # from given and add 1 for further operation
    l = len(str(max(array))) + 1
      
    # iterate given values and 
    # calculating extended values
    for i in array:
        temp = str(i) * l
          
        # make tuple of extended value and 
        # equivalant original value then 
        # append to list
        extval.append((temp[:l:], i))
      
    # sort extval in descending order
    extval.sort(reverse = True)
      
    # iterate extended values
    for i in extval:
          
        # concatinate original value equivalant
        # to extended value into ans variable
        ans += str(i[1])
  
    if int(ans)==0:
        return "0"
    return ans
  
# Driver code
a = [1, 34, 3, 98, 9, 76,
        45, 4, 12, 121]
  
print(largestNumber(a))
  
# This code is contributed by Chhekur

Producción:

99876454343121211

Este artículo es una contribución de Kondiparthi Shanmukha Sarath . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.