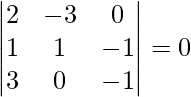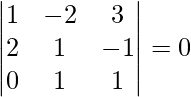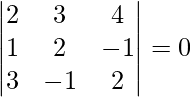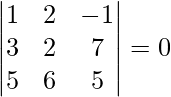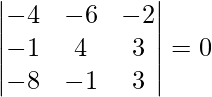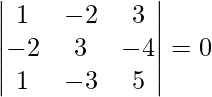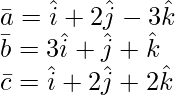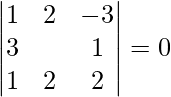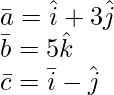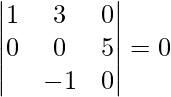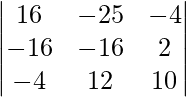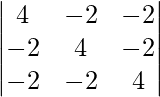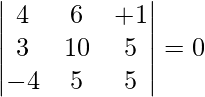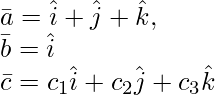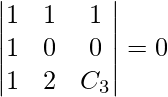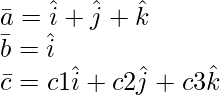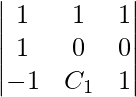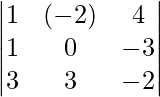Clase 12 Soluciones RD Sharma – Capítulo 26 Producto triple escalar – Ejercicio 26.1

Pregunta 1(i). Evalúa lo siguiente $[ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{ j}]$

Solución:

$[ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{ j}]$ = $( \sombrero{i} * \sombrero{j} ) . \sombrero{k} + ( \sombrero{j} * \sombrero{k} ) . \sombrero{i} + ( \sombrero{k} * \sombrero{i} ) . \hat{j}$

= $\hat{k} . \sombrero{k} + \sombrero{i} . \sombrero{i} + \sombrero{j} . \hat{j}$

= 1 + 1 + 1

= 3

Pregunta 1(ii). Evalúa lo siguiente $[ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat {j} \ 2\sombrero{i} ]$

Solución:

$[ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat{j} \ 2\hat{i} ]$ = $( \hat{2i} * \hat{j} ) . \hat{k} + ( \hat{i} * \hat{k} ) . \hat{j} + ( \hat{k} * \hat{j} ) .2\hat{i}$

= $2\hat{k}.\hat{k} + ( -\hat{j}).\hat{j} + ( -\hat{i} ).2\hat{i}$

= 2 – 1 – 2

= -1

Pregunta 2(i). encontrar $[ \bar{a}\ \bar{b}\ \bar{c} ]$ , cuando $\bar{a} = 2\hat{i} - 3\hat{j}, \bar{b} = \hat{i} + \hat{j} - \hat{k} \ and \ \bar{c} = 3\hat{i} - \hat{k}$

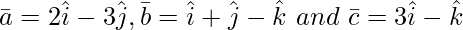
Solución:

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 2 & -3 & 0 \\ 1 & 1 & -1 \\ 3 & 0 & -1 \\ \end{vmatrix}= 0$

= 2(-1 – 0) + 3(-1 + 3)

= -2 + 6

= 4

Pregunta 2(ii). encontrar $[ \bar{a}\ \bar{b}\ \bar{c} ]$ , cuando $\bar{a} = \hat{i} - 2\hat{j} + 3\hat{k} , \bar{b} = 2\hat{i} + \hat{j} - \hat{k} \ and\ \bar{c} = \hat{j} + \hat{k}$

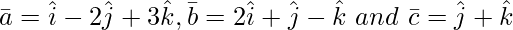
Solución:

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & -2 & 3 \\ 2 & 1 &-1 \\ 0 & 1 & 1 \\ \end{vmatrix} = 0$

= 1(1 + 1) + 2(2 + 0) + 3(2 – 0)

= 2 + 4 + 6

= 12

Pregunta 3(i). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector 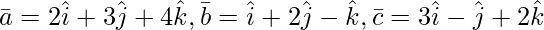$\bar{a} = 2\hat{i} + 3\hat{j} + 4\hat{k} , \bar{b} = \hat{i} + 2\hat{j} - \hat{k} , \bar{c} = 3\hat{i} - \hat{j} + 2\hat{k}$

Solución:

El volumen de un paralelepípedo cuyas aristas adyacentes son $\bar{a},\ \bar{b} ,\ \bar{c}$ es igual a $[ \bar{a}\ \bar{b}\ \bar{c} ]$

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 2 & 3 & 4 \\ 1 & 2 & -1 \\ 3 & -1 & 2 \\ \end{vmatrix} = 0$

= 2(4 – 1) – 3(2 + 3) + 4(-1 – 6)

= 6 – 15 – 28

= -9 – 28

= -37

Entonces, el volumen del paralelepípedo es | -37 | = 37 unidad cúbica.

Pregunta 3(ii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector 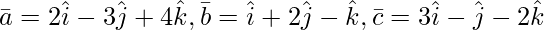$\bar{a} = 2\hat{i} - 3\hat{j} + 4\hat{k} , \bar{b} = \hat{i} + 2\hat{j} - \hat{k} , \bar{c} = 3\hat{i} - \hat{j} - 2\hat{k}$

Solución:

El volumen de un paralelepípedo cuyas aristas adyacentes $\bar{a},\ \bar{b} ,\ \bar{c}$ son es igual a $[ \bar{a}\ \bar{b}\ \bar{c} ]$

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 2 & -3 & 4 \\ 1 & 2 & -1 \\ 3 & -1& -2\end{vmatrix} = 0$

= 2(-4 – 1) + 3(-2 + 3) + 4(-1 – 6)

= -10 + 3 – 28

= -10 – 25

= -35

Entonces, Volumen del paralelepípedo = | -35 | = 35 unidad cúbica.

Pregunta 3(iii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector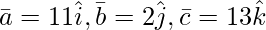 $\bar{a} = 11\hat{i}, \bar{b} = 2\hat{j} , \bar{c} = 13\hat{k}$

Solución:

Sea a = 11 $\hat{i}$ , b = 2 $\hat{j}$ , c = 13 $\hat{k}$

El volumen de un paralelepípedo cuyas aristas adyacentes son $\bar{a},\ \bar{b} ,\ \bar{c}$ es igual a $[ \bar{a}\ \bar{b}\ \bar{c} ]$

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 11 & 0& 0 \\ 0 & 2& 0 \\ 0 & 0& 13 \end{vmatrix} = 0$

= 11(26 – 0) + 0 + 0

= 286

Volumen de un paralelepípedo = | 286| = 286 unidades cúbicas.

Pregunta 3(iv). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector 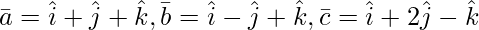$\bar{a} = \hat{i} + \hat{j} + \hat{k} , \bar{b} = \hat{i} - \hat{j} + \hat{k} , \bar{c} = \hat{i} + 2\hat{j} - \hat{k}$

Solución:

Dejar $\bar{a} = \hat{i} + \hat{j} + \hat{k} , \bar{b} = \hat{i} - \hat{j} + \hat{k} , \bar{c} = \hat{i} + 2\hat{j} - \hat{k}$

El volumen de un paralelepípedo cuyas aristas adyacentes $\bar{a},\ \bar{b} ,\ \bar{c}$ son es igual a $[ \bar{a}\ \bar{b}\ \bar{c} ]$

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & 1& 1 \\ 1 & -1& 1 \\ 1 & 2& -1 \end{vmatrix} = 0$

= 1(1 – 2) – 1(-1 – 1) + 1(2 + 1)

= -1 + 2 + 3

= 4

Volumen de un paralelepípedo = |4| = 4 unidades cúbicas.

Pregunta 4(i). La demostración de las siguientes tríadas de vector es coplanar: 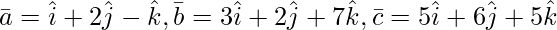$\bar{a} = \hat{i} + 2\hat{j} - \hat{k}, \bar{b} = 3\hat{i} + 2\hat{j} + 7\hat{k}, \bar{c} = 5\hat{i} + 6\hat{j} + 5\hat{k}$

Solución:

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & 2 & -1 \\ 3 & 2 & 7 \\ 5 & 6 & 5 \\ \end{vmatrix} = 0$

= 1(10 – 42) – 2(15 – 35) – 1(18 – 10)

= -32 + 40 – 8

= 0

Entonces, los vectores dados son coplanares.

Pregunta 4(ii). La demostración de las siguientes tríadas de vector es coplanar: 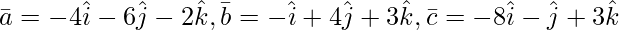$\bar{a} = -4\hat{i} - 6\hat{j} - 2\hat{k} , \bar{b} = -\hat{i} + 4\hat{j} + 3\hat{k} , \bar{c} = -8\hat{i} - \hat{j} + 3\hat{k}$

Solución:

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} -4 & -6 & -2 \\ -1 & 4 & 3 \\ -8 & -1 & 3 \\ \end{vmatrix} = 0$

= -4(12 + 3) + 6(-3 + 24) – 2(1 + 32)

= -60 + 126 – 66

= 0

Entonces, los vectores dados son coplanares.

Pregunta 4(iii). La demostración de las siguientes tríadas de vector es coplanar: 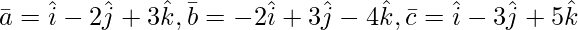$\bar{a} = \hat{i} - 2\hat{j} + 3\hat{k} , \bar{b} = -2\hat{i} + 3\hat{j} - 4\hat{k} , \bar{c} = \hat{i} - 3\hat{j} + 5\hat{k}$

Solución:

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & -2 & 3 \\ -2 & 3 & -4 \\ 1 & -3 & 5 \\ \end{vmatrix}=0$

= 1(15 – 12) + 2(-10 + 4) + 3(6 – 3)

= 3 – 12 + 9

= 0

Entonces, los vectores dados son coplanares.

Pregunta 5(i). Encuentre el valor de λ para que el siguiente vector sea coplanar: 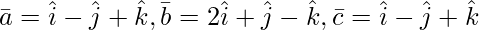$\bar{a} = \hat{i} - \hat{j} + \hat{k} , \bar{b} = 2\hat{i} + \hat{j} - \hat{k} , \bar{c} = λ\hat{i} - \hat{j} + λ\hat{k}$

Solución:

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & -1 & 1 \\ 2 & 1 &-1 \\ λ & -1 & λ \\ \end{vmatrix} = 0$

= 1(λ -1) + 1(2λ + λ) + 1(-2 – λ)

= λ – 1 + 3λ – 2 -λ

3 = 3λ

1 = l

Entonces, el valor de λ es 1

Pregunta 5(ii). Encuentre el valor de λ para que el siguiente vector sea coplanar: 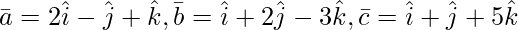$\bar{a} = 2\hat{i} - \hat{j} + \hat{k} , \bar{b} = \hat{i} + 2\hat{j} - 3\hat{k} , \bar{c} = λ\hat{i} + λ\hat{j} + 5\hat{k}$

Solución:

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 2 & -1 & 1 \\ 1 & 2 & -3 \\ λ & λ & 5 \\ \end{vmatrix} = 0$

= 2(10 + 3 λ) + 1(5 + 3 λ) + 1(λ – 2 λ)

= 20 + 6 λ + 5 + 3 λ – λ

-25 = 8 λ

λ = – 25 / 8

Entonces, el valor de λ es -25/8

Pregunta 5(iii). Encuentre el valor de λ para que el siguiente vector sea coplanar: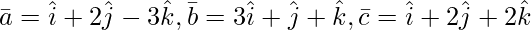 $\bar{a} = \hat{i} + 2\hat{j} - 3\hat{k} , \bar{b} = 3\hat{i} + λ\hat{j} + \hat{k} , \bar{c} = \hat{i} + 2\hat{j} + 2\hat{k}$

Solución:

Dado:

$\bar{a} = \hat{i} + 2\hat{j} - 3\hat{k} \\ \bar{b} = 3\hat{i} + λ\hat{j} + \hat{k} \\ \bar{c} = \hat{i} + 2\hat{j} + 2\hat{k}$

Como sabemos que tres vectores $\bar{a},\ \bar{b} ,\ \bar{c}$ son coplanares si sus $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0.

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & 2 & -3 \\ 3 & λ & 1 \\ 1 & 2 & 2 \\ \end{vmatrix} = 0$

= 1(2λ – 2) – 2(6 – 1) – 3(6 – λ)

= 2λ – 2 -12 + 2 -18 + 3λ

= 5λ – 30

30 = 5λ

λ = 6

Entonces, el valor de λ es 6

Pregunta 5(iv). Encuentre el valor de λ para que el siguiente vector sea coplanar: 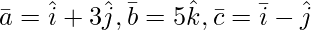$\bar{a} = \hat{i} + 3\hat{j} , \bar{b} = 5\hat{k} , \bar{c} = λ \bar{i} - \hat{j}$

Solución:

Dado:

$\bar{a} = \hat{i} + 3\hat{j} \\ \bar{b} = 5\hat{k} \\ \bar{c} = λ \bar{i} - \hat{j}$

Entonces, para probar que estos puntos son coplanares, tenemos que probar que $[ \bar{a}\ \bar{b}\ \bar{c} ]$ = 0

$[ \bar{a}\ \bar{b}\ \bar{c} ]$ = $\begin{vmatrix} 1 & 3 & 0 \\ 0 & 0 & 5 \\ λ & -1 & 0 \\ \end{vmatrix} = 0$

= 1(0 + 5) – 3(0 – 5λ) + 0

= 5 + 15λ

-5 = 15λ

λ = – 1 / 3

Pregunta 6. Muestre que los cuatro puntos que tienen vectores de posición 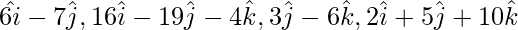$\hat{6i} - 7\hat{j} , 16\hat{i} - 19\hat{j} - 4\hat{k} , 3\hat{j} - 6\hat{k}, 2\hat{i} + 5\hat{j} + 10\hat{k}$ no son coplanares.

Solución:

Consideremos

AO = $6\hat{i} - 7\hat{j}$

OB = $16\hat{i} - 19\hat{j} - 4\hat{k}$

CO = $3\hat{j} - 6\hat{k}$

DE = $2\hat{i} + 5\hat{j} + 10\hat{k}$

AB = OB – OA = $16\hat{i} - 25\hat{j} - 4\hat{k}$

AC = CO – OA = $-16\hat{i} - 16\hat{j} + 2\hat{k}$

CD = OD – OC = $2\hat{i} + 2\hat{j} + 16\hat{k}$

AD = OD – OA = $4\hat{i} + 12\hat{j}+ 10\hat{k}$

Entonces, para probar que estos puntos son coplanares, tenemos que probar que $[\overline{AB} \ \overline{AC} \ \overline{AD} ] =0$

$\begin{vmatrix} 16 & -25 & -4 \\ -16& -16& 2 \\ -4 & 12 & 10 \\ \end{vmatrix}$

= 16(-160 – 24) + 25(-160 + 8) – 4(-144 + 64) ≠ 0

Por lo tanto, demostró que los puntos no son coplanares.

Pregunta 7. Demuestra que los puntos A (-1, 4, -3), B(3, 2, -5), C(-3, 8, -5) y D(-3, 2, 1) son coplanario

Solución:

Dado:

A = (-1, 4, -3)

B = (3, 2, -5)

C = (-3, 8, -5)

re = (-3, 2, 1)

$\overline{AB}$ = $4\hat{i} - 2\hat{j} - 2\hat{k}$

$\overline{AC}$ = $-2\hat{i} + 4\hat{j} - 2\hat{k}$

$\overline{AD}$ = $-2\hat{i} - 2\hat{j} + 4\hat{k}$

Entonces, para probar que estos puntos son coplanares, tenemos que probar que $[\overline{AB} \ \overline{AC} \ \overline{AD}] = 0$

De este modo, $\begin{vmatrix} 4 &-2 & -2 \\ -2& 4& -2 \\ -2 & -2& 4 \\ \end{vmatrix}$

= 4[16 – 4] + 2[-8 -4] – 2[4 + 8]

= 48 – 24 – 24 = 0

Por lo tanto, probado.

Pregunta 8. Muestre que cuatro puntos cuyos vectores de posición son 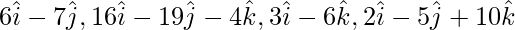$6\hat{i} - 7\hat{j} , 16\hat{i} - 19\hat{j} - 4\hat{k} , 3\hat{i} - 6\hat{k}, 2\hat{i} - 5\hat{j} + 10\hat{k}$

Solución:

Consideremos

AO = $6\hat{i} - 7\hat{j}$

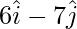
OB = $16\hat{i} - 19\hat{j} - 4\hat{k}$

CO = $3\hat{i} - 6\hat{k}$

DE = $2\hat{i} -5\hat{j} + 10\hat{k}$

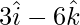
De este modo,

AB = OB – OA = $10\hat{i} - 12\hat{j} - 4\hat{k}$

AC = CO – OA = $-3\hat{i} + 7\hat{j}- 6\hat{k}$

AD = OD – OA = $-4\hat{i} + 2\hat{j} + 10\hat{k}$

Si los vectores AB, AC y AD son coplanares entonces los cuatro puntos son coplanares

Al simplificar, obtenemos

$\begin{vmatrix} 10 & -12 & -4 \\ -3 & 7 & -6\\ -4 & 2 & 10 \\ \end{vmatrix}$

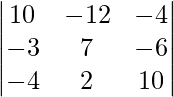
= 10(70 + 12) + 12(-30 – 24) – 4(-6 + 28)

= 820 – 648 – 88

= 84 ≠ 0

Entonces, los puntos no son coplanares.

Pregunta 9. Encuentra el valor de λ para el cual los cuatro puntos con vectores de posición 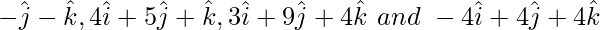$-\hat{j} - \hat{k}, 4\hat{i} + 5\hat{j} + λ \hat{k}, 3\hat{i} + 9\hat{j} + 4\hat{k}\ and\ -4\hat{i} + 4\hat{j} + 4\hat{k}$ son coplanares

Solución:

Consideremos:

Vector de posición de A = $-\hat{j} -\hat{k}$

Vector de posición de B = $4\hat{i} + 5\hat{j} + λ\hat{k}$

Vector de posición de C = $3\hat{i} + 9\hat{j} + 4\hat{k}$

Vector de posición de D = $-4\hat{i} + 4\hat{j} + 4\hat{k}$

Si los vectores dados $\overline{AB},\ \overline{AC}, \ \overline{AD}$ son coplanares, entonces los cuatro puntos son coplanares

$\overline{AB}$ = $4\hat{i} + 6\hat{j} + ( λ + 1 ) \hat{k}$

$\overline{AC}$ = $3\hat{i} + 10\hat{j} + 5\hat{k}$

$\overline{AD}$ = $-4\hat{i} + 5\hat{j} + 5\hat{k}$

Al simplificar, obtenemos

$\begin{vmatrix} 4 & 6 & λ+1 \\ 3 & 10 & 5 \\ -4 & 5 & 5 \end{vmatrix} = 0$

4(50 – 25) – 6(15 + 20) + (λ + 1)(15 + 40) = 0

100 – 210 + 55 + 55λ = 0

55λ = 55

l = 1

Entonces, cuando el valor de λ = 1, los puntos dados son coplanares.

Pregunta 10. Demuestra que $( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0$

Solución:

Dado: $( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0$

Una resolviendo la ecuación dada obtenemos

= $[ ( \bar{a} - \bar{b} ) ( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ]$

= $[ a( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ] + [ -b ( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ]$

= 6 [ un segundo c ] – 6 [ un segundo c ]

= 0

Por lo tanto probado

Cuestión 11. $\bar{a} , \bar{b} ,\bar{c}$ Son los vectores de posición de los puntos A, B y C respectivamente, demuestre que $\bar{a} * \bar{b} + \bar{b} * \bar{c} + \bar{c} * \bar{a}$ es un vector perpendicular al plano del triángulo ABC.

Solución:

En el triángulo ABC dado,

Si $\bar{a}$ = AB

$\bar{b}$ = BC

$\bar{c}$ = CA

Después,

$\bar{a} * \bar{b}$ es perpendicular al plano del triángulo ABC dado

$\bar{b} * \bar{c}$ es perpendicular al plano del triángulo ABC dado

$\bar{c} * \bar{a}$ es perpendicular al plano del triángulo ABC dado

Por lo tanto, demostró que $\bar{a} * \bar{b} + \bar{b} * \bar{c} + \bar{c} * \bar{a}$

es un vector perpendicular al plano del triángulo ABC dado.

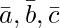Pregunta 12(i). deja $\bar{a} = \hat{i} + \hat{j} + \hat{k}, \ \bar{b} = \hat{i} \ and \ \bar{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$ _ Entonces, si c ₁ = 1 y c ₂ = 2, encuentre c ₃ que sea $\bar{a}, \bar{b}, \bar{c}$ coplanar.

Solución:

Dado:

$\bar{a} = \hat{i} + \hat{j} + \hat{k}, \\ \bar{b} = \hat{i} \\ \bar{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$

$\bar{a}, \bar{b}, \bar{c}$ son coplanares solo si $[\bar{a}, \bar{b}, \bar{c}]$ = 0

$\begin{vmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 2 & C_3 \end{vmatrix} = 0$

0 – 1(C ₃ ) + 1(2) = 0

C ₃ = 2

Entonces, cuando el valor C ₃ = 2, entonces estos puntos son coplanares.

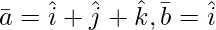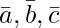Pregunta 12(ii). Sea $\bar{a} = \hat{i}+\hat{j}+\hat{k}, \bar{b} = \hat{i}$ y $\bar{c} = c1\hat{i} + c2\hat{j} + c3\hat{k}$ . Entonces, si c2 = -1 y c3 =1, demuestre que ningún valor de c ₁ puede hacer $\bar{a}, \bar{b}, \bar{c}$ coplanar

Solución:

Dado:

$\bar{a} = \hat{i}+\hat{j}+\hat{k}\\ \bar{b} = \hat{i}\\ \bar{c} = c1\hat{i} + c2\hat{j} + c3\hat{k}$

$\bar{a}, \bar{b}, \bar{c}$ son coplanares solo si $[\bar{a}, \bar{b}, \bar{c}]$ = 0

Asi que,

$\begin{vmatrix} 1 & 1 & 1\\ 1 & 0 & 0\\ -1& C_1& 1\end{vmatrix}$

0 – 1 + 1 (C ₁ ) = 0

C1 = ₁

Por lo tanto, demuestre que ningún valor de C ₁ puede hacer que estos puntos sean coplanarios .

Pregunta 13. Encuentra λ para el cual los puntos A (3, 2, 1), B (4, λ, 5), C (4, 2, -2) y D (6, 5, -1) son coplanares

Solución:

Consideremos:

Vector de posición de OA = $3\hat{i} + 2\hat{j}+ \hat{k}$

Vector de posición del OB = $4\hat{i} + λ\hat{j} + 5\hat{k}$

Vector de posición de OC = $4\hat{i} + 2\hat{j} - 2\hat{k}$

Vector de posición de OD = $6\hat{i} + 5\hat{j} - \hat{k}$

Si los vectores AB, AC y AD son coplanares, entonces los cuatro puntos son coplanares

AB = $\hat{i} + ( λ - 2 ) \hat{j} + 4\hat{k}$

CA = $\hat{i} + 0\hat{j} - 3\hat{k}$

DA = $3\hat{i} + 3\hat{j} - 2\hat{k}$

Al simplificar, obtenemos

$\begin{vmatrix} 1 & ( λ - 2 ) & 4 \\ 1 & 0 & -3 \\ 3 & 3 & -2 \\ \end{vmatrix}$

1(9) – (λ – 2)(-2 + 9) + 4(3 – 0) = 0

9 – 7 λ + 14 + 12 = 0

7 λ = 35

λ = 5

Por lo tanto, el valor de λ es 5. Entonces, los puntos coplanares son A(3, 2, 1), B(4, 5, 5), C(4, 2, -2) y D(6, 5, -1)

Publicación traducida automáticamente

Artículo escrito por vishnuteja476 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1(i). Evalúa lo siguiente

Pregunta 1(ii). Evalúa lo siguiente

Pregunta 2(i). encontrar , cuando

Pregunta 2(ii). encontrar , cuando

Pregunta 3(i). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector

Pregunta 3(ii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector

Pregunta 3(iii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector

Pregunta 3(iv). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector

Pregunta 4(i). La demostración de las siguientes tríadas de vector es coplanar:

Pregunta 4(ii). La demostración de las siguientes tríadas de vector es coplanar:

Pregunta 4(iii). La demostración de las siguientes tríadas de vector es coplanar:

Pregunta 5(i). Encuentre el valor de λ para que el siguiente vector sea coplanar:

Pregunta 5(ii). Encuentre el valor de λ para que el siguiente vector sea coplanar:

Pregunta 5(iii). Encuentre el valor de λ para que el siguiente vector sea coplanar:

Pregunta 5(iv). Encuentre el valor de λ para que el siguiente vector sea coplanar:

Pregunta 6. Muestre que los cuatro puntos que tienen vectores de posición no son coplanares.

Pregunta 7. Demuestra que los puntos A (-1, 4, -3), B(3, 2, -5), C(-3, 8, -5) y D(-3, 2, 1) son coplanario

Pregunta 8. Muestre que cuatro puntos cuyos vectores de posición son

Pregunta 9. Encuentra el valor de λ para el cual los cuatro puntos con vectores de posición son coplanares

Pregunta 10. Demuestra que

Cuestión 11. Son los vectores de posición de los puntos A, B y C respectivamente, demuestre que es un vector perpendicular al plano del triángulo ABC.

Pregunta 12(i). deja _ Entonces, si c 1 = 1 y c 2 = 2, encuentre c 3 que sea coplanar.

Pregunta 12(ii). Sea y . Entonces, si c2 = -1 y c3 =1, demuestre que ningún valor de c 1 puede hacer coplanar

Pregunta 13. Encuentra λ para el cual los puntos A (3, 2, 1), B (4, λ, 5), C (4, 2, -2) y D (6, 5, -1) son coplanares

Deja una respuesta Cancelar la respuesta

Pregunta 1(i). Evalúa lo siguiente $[ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{ j}]$

Pregunta 1(ii). Evalúa lo siguiente $[ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat {j} \ 2\sombrero{i} ]$

Pregunta 2(i). encontrar $[ \bar{a}\ \bar{b}\ \bar{c} ]$ , cuando $\bar{a} = 2\hat{i} - 3\hat{j}, \bar{b} = \hat{i} + \hat{j} - \hat{k} \ and \ \bar{c} = 3\hat{i} - \hat{k}$

Pregunta 2(ii). encontrar $[ \bar{a}\ \bar{b}\ \bar{c} ]$ , cuando $\bar{a} = \hat{i} - 2\hat{j} + 3\hat{k} , \bar{b} = 2\hat{i} + \hat{j} - \hat{k} \ and\ \bar{c} = \hat{j} + \hat{k}$

Pregunta 3(i). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector $\bar{a} = 2\hat{i} + 3\hat{j} + 4\hat{k} , \bar{b} = \hat{i} + 2\hat{j} - \hat{k} , \bar{c} = 3\hat{i} - \hat{j} + 2\hat{k}$

Pregunta 3(ii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector $\bar{a} = 2\hat{i} - 3\hat{j} + 4\hat{k} , \bar{b} = \hat{i} + 2\hat{j} - \hat{k} , \bar{c} = 3\hat{i} - \hat{j} - 2\hat{k}$

Pregunta 3(iii). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector $\bar{a} = 11\hat{i}, \bar{b} = 2\hat{j} , \bar{c} = 13\hat{k}$

Pregunta 3(iv). Encuentre el volumen del paralelepípedo cuyas aristas colindantes están representadas por el vector $\bar{a} = \hat{i} + \hat{j} + \hat{k} , \bar{b} = \hat{i} - \hat{j} + \hat{k} , \bar{c} = \hat{i} + 2\hat{j} - \hat{k}$

Pregunta 4(i). La demostración de las siguientes tríadas de vector es coplanar: $\bar{a} = \hat{i} + 2\hat{j} - \hat{k}, \bar{b} = 3\hat{i} + 2\hat{j} + 7\hat{k}, \bar{c} = 5\hat{i} + 6\hat{j} + 5\hat{k}$

Pregunta 4(ii). La demostración de las siguientes tríadas de vector es coplanar: $\bar{a} = -4\hat{i} - 6\hat{j} - 2\hat{k} , \bar{b} = -\hat{i} + 4\hat{j} + 3\hat{k} , \bar{c} = -8\hat{i} - \hat{j} + 3\hat{k}$

Pregunta 4(iii). La demostración de las siguientes tríadas de vector es coplanar: $\bar{a} = \hat{i} - 2\hat{j} + 3\hat{k} , \bar{b} = -2\hat{i} + 3\hat{j} - 4\hat{k} , \bar{c} = \hat{i} - 3\hat{j} + 5\hat{k}$

Pregunta 5(i). Encuentre el valor de λ para que el siguiente vector sea coplanar: $\bar{a} = \hat{i} - \hat{j} + \hat{k} , \bar{b} = 2\hat{i} + \hat{j} - \hat{k} , \bar{c} = λ\hat{i} - \hat{j} + λ\hat{k}$

Pregunta 5(ii). Encuentre el valor de λ para que el siguiente vector sea coplanar: $\bar{a} = 2\hat{i} - \hat{j} + \hat{k} , \bar{b} = \hat{i} + 2\hat{j} - 3\hat{k} , \bar{c} = λ\hat{i} + λ\hat{j} + 5\hat{k}$

Pregunta 5(iii). Encuentre el valor de λ para que el siguiente vector sea coplanar: $\bar{a} = \hat{i} + 2\hat{j} - 3\hat{k} , \bar{b} = 3\hat{i} + λ\hat{j} + \hat{k} , \bar{c} = \hat{i} + 2\hat{j} + 2\hat{k}$

Pregunta 5(iv). Encuentre el valor de λ para que el siguiente vector sea coplanar: $\bar{a} = \hat{i} + 3\hat{j} , \bar{b} = 5\hat{k} , \bar{c} = λ \bar{i} - \hat{j}$

Pregunta 6. Muestre que los cuatro puntos que tienen vectores de posición $\hat{6i} - 7\hat{j} , 16\hat{i} - 19\hat{j} - 4\hat{k} , 3\hat{j} - 6\hat{k}, 2\hat{i} + 5\hat{j} + 10\hat{k}$ no son coplanares.

Pregunta 8. Muestre que cuatro puntos cuyos vectores de posición son $6\hat{i} - 7\hat{j} , 16\hat{i} - 19\hat{j} - 4\hat{k} , 3\hat{i} - 6\hat{k}, 2\hat{i} - 5\hat{j} + 10\hat{k}$

Pregunta 9. Encuentra el valor de λ para el cual los cuatro puntos con vectores de posición $-\hat{j} - \hat{k}, 4\hat{i} + 5\hat{j} + λ \hat{k}, 3\hat{i} + 9\hat{j} + 4\hat{k}\ and\ -4\hat{i} + 4\hat{j} + 4\hat{k}$ son coplanares

Pregunta 10. Demuestra que $( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0$

Cuestión 11. $\bar{a} , \bar{b} ,\bar{c}$ Son los vectores de posición de los puntos A, B y C respectivamente, demuestre que $\bar{a} * \bar{b} + \bar{b} * \bar{c} + \bar{c} * \bar{a}$ es un vector perpendicular al plano del triángulo ABC.

Pregunta 12(i). deja $\bar{a} = \hat{i} + \hat{j} + \hat{k}, \ \bar{b} = \hat{i} \ and \ \bar{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$ _ Entonces, si c ₁ = 1 y c ₂ = 2, encuentre c ₃ que sea $\bar{a}, \bar{b}, \bar{c}$ coplanar.

Pregunta 12(ii). Sea $\bar{a} = \hat{i}+\hat{j}+\hat{k}, \bar{b} = \hat{i}$ y $\bar{c} = c1\hat{i} + c2\hat{j} + c3\hat{k}$ . Entonces, si c2 = -1 y c3 =1, demuestre que ningún valor de c ₁ puede hacer $\bar{a}, \bar{b}, \bar{c}$ coplanar