m-WAY Buscar Árboles | Set-1 (Buscando)

Los árboles de búsqueda m-way son árboles multidireccionales que son versiones generalizadas de árboles binarios donde cada Node contiene múltiples elementos. En un árbol de vías m de orden m , cada Node contiene un máximo de m – 1 elementos y m hijos.
El objetivo del árbol de búsqueda m-Way de altura h requiere O(h) no. de accesos para una operación de inserción/eliminación/recuperación. Por lo tanto, asegura que la altura h esté cerca de log_m(n + 1) .
El número de elementos en un árbol de búsqueda m-Way de altura h varía desde un mínimo de h hasta un máximo de  .
Un árbol de búsqueda m-Way de n elementos varía desde una altura mínima delog_m(n+1) hasta un máximo de n
En la siguiente figura se muestra un ejemplo de un árbol de búsqueda de 5 vías. Observe cómo cada Node tiene como máximo 5 Nodes secundarios y, por lo tanto, tiene como máximo 4 claves contenidas en él. 
 

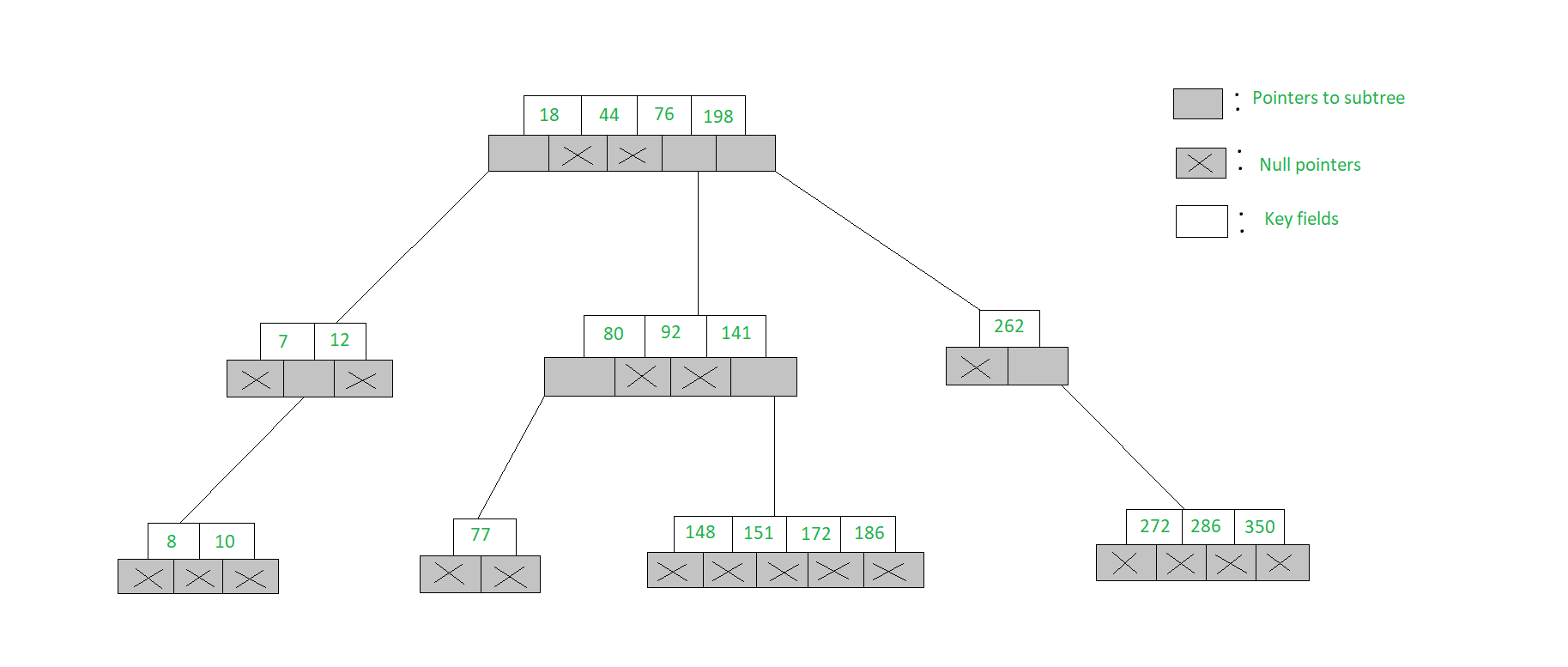
La estructura de un Node de un árbol m-Way se da a continuación: 
 

struct node {
    int count;
    int value[MAX + 1];
    struct node* child[MAX + 1];
};

public class Node {
    int count;
    int[] value = new int[MAX + 1];
    Node[] child = new Node[MAX + 1];
}
 
// This code is contributed by tapeshdua420.

class node:
    def __init__(self):
        self.count = -1
        self.value = [-1]*(MAX + 1)
        self.child = [None]*(MAX + 1)

class node {
    public int count;
    public int[] value = new int[MAX + 1];
    public node[] child = new node[MAX + 1];
}
 
// This code is contributed by Tapesh (tapeshdua420)

• Aquí, count representa el número de hijos que tiene un Node en particular
• Los valores de un Node almacenados en el valor de la array
• Las direcciones de los Nodes secundarios se almacenan en la array secundaria
• La macro MAX significa el número máximo de valores que un Node en particular puede contener

Búsqueda en un árbol de búsqueda de m-Way: 
 

• La búsqueda de una clave en un árbol de búsqueda m-Way es similar a la de un árbol de búsqueda binaria
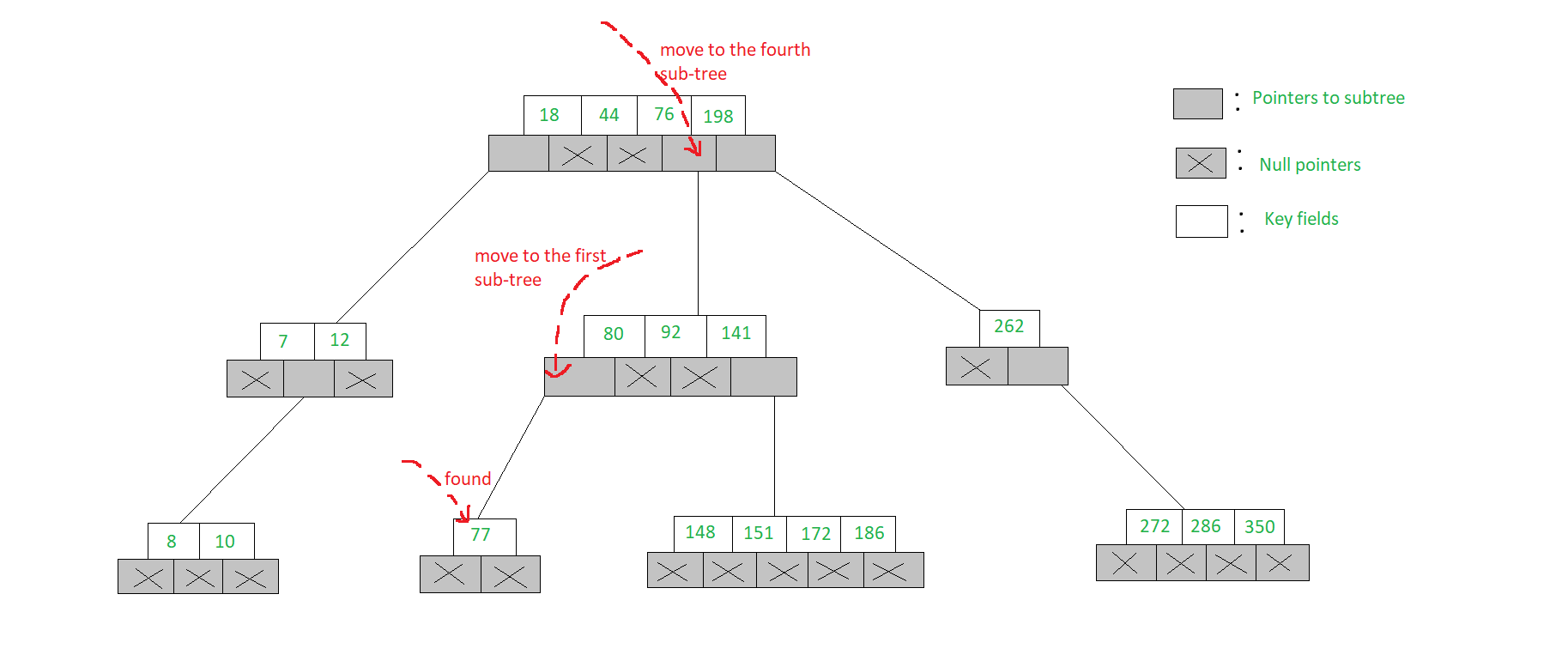
• Para buscar 77 en el árbol de búsqueda de 5 vías, que se muestra en la figura, comenzamos en la raíz y como 77> 76> 44> 18, pasamos al cuarto subárbol
• En el Node raíz del cuarto subárbol, 77< 80 y por lo tanto pasamos al primer subárbol del Node. Dado que 77 está disponible en el único Node de este subárbol, afirmamos que 77 se buscó con éxito

// Searches value in the node
struct node* search(int val,
                    struct node* root,
                    int* pos)
{
 
    // if root is Null then return
    if (root == NULL)
        return NULL;
    else {
 
        // if node is found
        if (searchnode(val, root, pos))
            return root;
 
        // if not then search in child nodes
        else
            return search(val,
                          root->child[*pos],
                          pos);
    }
}
 
// Searches the node
int searchnode(int val,
               struct node* n,
               int* pos)
{
    // if val is less than node->value[1]
    if (val < n->value[1]) {
        *pos = 0;
        return 0;
    }
 
    // if the val is greater
    else {
        *pos = n->count;
 
        // check in the child array
        // for correct position
        while ((val < n->value[*pos])
               && *pos > 1)
            (*pos)--;
        if (val == n->value[*pos])
            return 1;
        else
            return 0;
    }
}

// Searches value in the node
public Node search(int val, Node root, int pos) {
    // if root is Null then return
    if (root == null)
        return null;
    else {
        // if node is found
        if (searchnode(val, root, pos))
            return root;
             
        // if not then search in child nodes
        else
            return search(val, root.child[pos], pos);
    }
}
 
// Searches the node
public boolean searchnode(int val, Node n, int pos) {
    // if val is less than node.value[1]
    if (val < n.value[1]) {
        pos = 0;
        return false;
    }
     // if the val is greater
    else {
        pos = n.count;
         
        // check in the child array
        // for correct position
        while ((val < n.value[pos]) && pos > 1)
            pos--;
             
        if (val == n.value[pos])
            return true;
        else
            return false;
    }
}
 
// This code is contributed by Tapesh(tapeshdua420)

# Searches value in the node
def search(val, root, pos):
 
    # if root is None then return
    if (root == None):
        return None
    else :
        # if node is found
        if (searchnode(val, root, pos)):
            return root
 
        # if not then search in child nodes
        else:
            return search(val, root.child[pos], pos)
     
 
 
# Searches the node
def searchnode(val, n, pos):
    # if val is less than node.value[1]
    if (val < n.value[1]):
        pos = 0
        return 0
     
 
    # if the val is greater
    else :
        pos = n.count
 
        # check in the child array
        # for correct position
        while ((val < n.value[pos]) and pos > 1):
            pos-=1
        if (val == n.value[pos]):
            return 1
        else:
            return 0
    

// Searches value in the node
public Node search(int val, Node root, int pos)
{
    // if root is Null then return
    if (root == null)
        return null;
    else {
        // if node is found
        if (searchnode(val, root, pos))
            return root;
 
        // if not then search in child nodes
        else
            return search(val, root.child[pos], pos);
    }
}
 
// Searches the node
public bool searchnode(int val, Node n, int pos)
{
    // if val is less than node.value[1]
    if (val < n.value[1]) {
        pos = 0;
        return false;
    }
 
    // if the val is greater
    else {
        pos = n.count;
 
        // check in the child array
        // for correct position
        while ((val < n.value[pos]) && pos > 1)
            pos--;
 
        if (val == n.value[pos])
            return true;
        else
            return false;
    }
}
 
// This code is contributed by Tapesh (tapeshdua420)

búsqueda(): 
 

• La función search() recibe tres parámetros
• El primer parámetro es el valor a buscar, el segundo es la dirección del Node desde donde se realizará la búsqueda y el tercero es la dirección de una variable que se utiliza para almacenar la posición del valor una vez encontrado.
• Inicialmente se verifica una condición si la dirección del Node que se busca es NULL
• Si es así, simplemente se devuelve un valor NULL
• De lo contrario, se llama a una función searchnode() que realmente busca el valor dado
• Si la búsqueda tiene éxito, se devuelve la dirección del Node en el que se encuentra el valor.
• Si la búsqueda no tiene éxito, se realiza una llamada recursiva a la función de búsqueda() para el hijo del Node actual

Node de búsqueda(): 
 

• La función searchnode() recibe tres parámetros
• El primer parámetro es el valor que se va a buscar.
• El segundo parámetro es la dirección del Node en el que se va a realizar la búsqueda y el tercero es un puntero pos que contiene la dirección de una variable en la que se almacena la posición del valor que una vez encontrado
• Esta función devuelve un valor 0 si la búsqueda no tiene éxito y 1 si tiene éxito
• En esta función inicialmente se comprueba si el valor que se va a buscar es menor que el primer valor del Node
• Si es así, indica que el valor no está presente en el Node actual. Por lo tanto, se asigna un valor 0 en la variable a la que apunta pos y se devuelve 0, ya que la búsqueda no tiene éxito.