Dado un árbol infinito y tres números N, M y X que tiene exactamente N hijos de cada Node. Cada arista tiene un peso de 1, 2, 3, 4..N. La tarea es encontrar el conteo de caminos cuyo peso es exactamente X y tiene un mínimo de un borde de peso M en él.
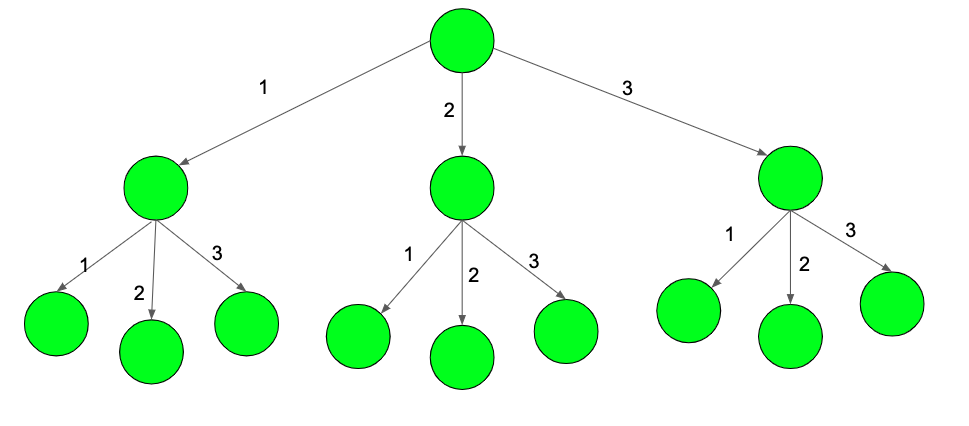
El diagrama de arriba muestra un árbol que se muestra hasta el nivel 3 y N = 3.
Ejemplos:
Input: N = 3, M = 2, X = 3 Output: 2 The path 1-2 and 2-1 in the image above Input: N = 2, M = 1, X = 4 Output: 4
Enfoque: El problema se puede resolver usando Programación Dinámica y memorización . Utilizaremos un enfoque de arriba hacia abajo para resolver este problema. Repita comenzando desde la raíz con la suma inicialmente como X, y recorra recursivamente todos los caminos posibles (que es de 1 a N). Si el Node es igual a M, entonces el segundo parámetro se vuelve verdadero, de lo contrario, permanece igual al que se pasó en la llamada anterior. Almacene el valor en una tabla DP[][] para evitar visitar los mismos estados dos veces.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to count the number of paths
#include <bits/stdc++.h>
using namespace std;
#define max 4
#define c 2
// Function to find the number of paths
int countPaths(int sum, int get, int m, int n, int dp[])
{
// If the summation is more than X
if (sum < 0)
return 0;
// If exactly X weights have reached
if (sum == 0)
return get;
// Already visited
if (dp[sum][get] != -1)
return dp[sum][get];
// Count paths
int res = 0;
// Traverse in all paths
for (int i = 1; i <= n; i++) {
// If the edge weight is M
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else // Edge's weight is not M
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
// Driver Code
int main()
{
int n = 3, m = 2, x = 3;
int dp[max + 1];
// Initialized the DP array with -1
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i][j] = -1;
// Function to count paths
cout << countPaths(x, 0, m, n, dp);
}
Java
// Java program to count the number of paths
public class GFG{
static int max = 4 ;
static int c = 2 ;
// Function to find the number of paths
static int countPaths(int sum, int get, int m, int n, int dp[][])
{
// If the summation is more than X
if (sum < 0)
return 0;
// If exactly X weights have reached
if (sum == 0)
return get;
// Already visited
if (dp[sum][get] != -1)
return dp[sum][get];
// Count paths
int res = 0;
// Traverse in all paths
for (int i = 1; i <= n; i++) {
// If the edge weight is M
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else // Edge's weight is not M
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
// Driver Code
public static void main(String []args)
{
int n = 3, m = 2, x = 3;
int dp[][] = new int[max + 1][2];
// Initialized the DP array with -1
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i][j] = -1;
// Function to count paths
System.out.println(countPaths(x, 0, m, n, dp));
}
// This code is contributed by Ryuga
}
Python3
# Python3 program to count the number of paths Max = 4 c = 2 # Function to find the number of paths def countPaths(Sum, get, m, n, dp): # If the Summation is more than X if (Sum < 0): return 0 # If exactly X weights have reached if (Sum == 0): return get # Already visited if (dp[Sum][get] != -1): return dp[Sum][get] # Count paths res = 0 # Traverse in all paths for i in range(1, n + 1): # If the edge weight is M if (i == m): res += countPaths(Sum - i, 1, m, n, dp) else: # Edge's weight is not M res += countPaths(Sum - i, get, m, n, dp) dp[Sum][get] = res return dp[Sum][get] # Driver Code n = 3 m = 2 x = 3 dp = [[-1 for i in range(2)] for i in range(Max + 1)] # Initialized the DP array with -1 for i in range(Max + 1): for j in range(2): dp[i][j] = -1 # Function to count paths print(countPaths(x, 0, m, n, dp)) # This code is contributed by Mohit kumar 29
C#
// C# program to count the number of paths
using System;
class GFG
{
static int max = 4 ;
static int c = 2 ;
// Function to find the number of paths
static int countPaths(int sum, int get, int m,
int n, int[, ] dp)
{
// If the summation is more than X
if (sum < 0)
return 0;
// If exactly X weights have reached
if (sum == 0)
return get;
// Already visited
if (dp[sum, get] != -1)
return dp[sum, get];
// Count paths
int res = 0;
// Traverse in all paths
for (int i = 1; i <= n; i++)
{
// If the edge weight is M
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else // Edge's weight is not M
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum, get] = res;
return dp[sum, get];
}
// Driver Code
public static void Main()
{
int n = 3, m = 2, x = 3;
int[,] dp = new int[max + 1, 2];
// Initialized the DP array with -1
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i, j] = -1;
// Function to count paths
Console.WriteLine(countPaths(x, 0, m, n, dp));
}
}
// This code is contributed by Akanksha Rai
PHP
<?php
// PHP program to count the number of paths
$max = 4;
$c = 2;
// Function to find the number of paths
function countPaths($sum, $get, $m, $n, &$dp)
{
global $max,$c;
// If the summation is more than X
if ($sum < 0)
return 0;
// If exactly X weights have reached
if ($sum == 0)
return $get;
// Already visited
if ($dp[$sum][$get] != -1)
return $dp[$sum][$get];
// Count paths
$res = 0;
// Traverse in all paths
for ($i = 1; $i <= $n; $i++)
{
// If the edge weight is M
if ($i == $m)
$res += countPaths($sum - $i, 1, $m, $n, $dp);
else // Edge's weight is not M
$res += countPaths($sum - $i, $get, $m, $n, $dp);
}
$dp[$sum][$get] = $res;
return $dp[$sum][$get];
}
// Driver Code
$n = 3;
$m = 2;
$x = 3;
$dp = array_fill(0,$max + 1,NULL);
// Initialized the DP array with -1
for ($i = 0; $i <= $max; $i++)
for ($j = 0; $j < 2; $j++)
$dp[$i][$j] = -1;
// Function to count paths
echo countPaths($x, 0, $m, $n, $dp);
// This code is contributed by ChitraNayal
?>
Javascript
<script>
// Javascript program to count the number of paths
let max = 4;
let c = 2;
// Function to find the number of paths
function countPaths(sum, get, m, n, dp)
{
// If the summation is more than X
if (sum < 0)
return 0;
// If exactly X weights have reached
if (sum == 0)
return get;
// Already visited
if (dp[sum][get] != -1)
return dp[sum][get];
// Count paths
let res = 0;
// Traverse in all paths
for(let i = 1; i <= n; i++)
{
// If the edge weight is M
if (i == m)
res += countPaths(sum - i, 1,
m, n, dp);
// Edge's weight is not M
else
res += countPaths(sum - i, get,
m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
// Driver Code
let n = 3, m = 2, x = 3;
let dp = new Array(max + 1);
// Initialized the DP array with -1
for(let i = 0; i <= max; i++)
{
dp[i] = new Array(2)
for(let j = 0; j < 2; j++)
dp[i][j] = -1;
}
// Function to count paths
document.write(countPaths(x, 0, m, n, dp));
// This code is contributed by avanitrachhadiya2155
</script>
2
Complejidad de tiempo: O (x * n), ya que estamos usando un ciclo para atravesar n veces y en cada recorrido, estamos llamando recursivamente a la función nuevamente, lo que costará O (x). Donde n es el número de hijos de cada Node y x es el peso total.
Espacio Auxiliar: O(x*n), ya que estamos usando espacio extra para la array DP . Donde n es el número de hijos de cada Node y x es el peso total.