Teorema maestro para restar y conquistar recurrencias

El teorema maestro se usa para determinar el límite superior Big – O en funciones que poseen recurrencia, es decir, que se pueden dividir en subproblemas. 
Teorema maestro para restar y conquistar recurrencias : 
Sea T(n) una función definida en n positiva como se muestra a continuación: 
 

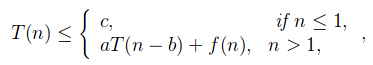
para algunas constantes c, a>0, b>0, k>=0 y función f(n). Si f(n) es O(n ^k ), entonces
1. Si a<1 entonces T(n) = O(n ^k ) 
2. Si a=1 entonces T(n) = O(n ^k+1 ) 
3 Si a>1 entonces T(n) = O(n ^k a ^n/b )
Prueba del teorema anterior (Por método de sustitución) :
De la función anterior, tenemos: 
T(n) = aT(nb) + f(n ) 
T(nb) = aT(n-2b) + f(nb) 
T(n-2b) = aT(n-3b) + f(n-2b)
Ahora, 
T(nb) = a ² T(n- 3b) + af(n-2b) + f(nb) 
T(n) = a ³ T(n-3b) + a ² f(n-2b) + af(nb) + f(n) 
T(n) = Σ ^{i=0 a n} aⁱ f(n-ib) + constante, donde f(n-ib) es O(n-ib) 
T(n) = O(n ^k Σ ^{i=0 to n/b} a ⁱ )

 
Donde, 
si a<1 entonces Σ ^{i=0 a n/b} a ⁱ = O(1), T(n) = O(n ^k )
Si a=1 entonces Σ ^{i=0 a n/b} a ⁱ = O (n), T(n) = O(n ^k+1 ) 
Si a>1 entonces Σ ^{i=0 to n/b} a ⁱ = O(a ^n/b ), T(n) = O(n ^k a ^n/b )
Considere el siguiente programa para el n-ésimo número de fibonacci : 
 

#include<stdio.h>
int fib(int n)
{
   if (n <= 1)
      return n;
   return fib(n-1) + fib(n-2);
}
  
int main ()
{
  int n = 9;
  printf("%d", fib(n));
  getchar();
  return 0;
}

# Python3 code for the above approach
def fib(n):
    if (n <= 1):
        return n
    return fib(n - 1) + fib(n - 2)
 
# Driver code
n = 9
print(fib(n))
 
# This code is contributed
# by sahishelangia

//Java code for above the approach.
class clg
{
 static int fib(int n)
{
if (n <= 1)
    return n;
return fib(n-1) + fib(n-2);
}
// Driver Code
public static void main (String[] args)
{
int n = 9;
System.out.println( fib(n));
}
}
// This code is contributed by Mukul Singh.

// C# code for above the approach.
using System;
     
class GFG
{
    static int fib(int n)
    {
        if (n <= 1)
            return n;
        return fib(n - 1) + fib(n - 2);
    }
     
    // Driver Code
    public static void Main(String[] args)
    {
        int n = 9;
        Console.WriteLine(fib(n));
    }
}
 
// This code has been contributed
// by Rajput-Ji

<?php
// PHP code for the above approach
function fib($n)
{
    if ($n <= 1)
        return $n;
    return fib($n - 1) +
           fib($n - 2);
}
 
// Driver Code
$n = 9;
echo fib($n);
 
// This code is contributed
// by Akanksha Rai
?>

<script>
    // Javascript code for above the approach.
     
    function fib(n)
    {
        if (n <= 1)
            return n;
        return fib(n - 1) + fib(n - 2);
    }
     
    let n = 9;
      document.write(fib(n));
     
</script>

Producción 
 

34

Análisis de la complejidad del tiempo: 
la función recursiva se puede definir como T(n) = T(n-1) + T(n-2) 
 

• Para el peor de los casos, sea T(n-1) ≈ T(n-2) 
  T(n) = 2T(n-1) + c 
  donde,f(n) = O(1) 
  ∴ k=0, a=2 ,b=1;
  T(n) = O(n ⁰ 2 ^n/1 ) 
  = O(2 ⁿ ) 
   
• Para el mejor de los casos, sea T(n-2) ≈ T(n-1) 
  T(n) = 2T(n-2) + c 
  donde,f(n) = O(1) 
  ∴ k=0, a=2 ,b=2;
  T(n) = O(n ⁰ 2 ^n/2 ) 
  = O(2 ^n/2 ) 
   

Más ejemplos :

• Ejemplo-1 : 
  T(n) = 3T(n-1), n>0 
       = c, n<=0
  Sol:a=3, b=1, f(n)=0 entonces k=0;
  Como a>0, T(n) = O(n ^k a ^n/b ) 
  T(n)= O(n ⁰ 3 ^n/1 ) 
  T(n)= 3 ⁿ 
   
• Ejemplo-2 : 
  T(n) = T(n-1) + n(n-1), si n>=2 
       = 1, si n=1
  Sol:a=1, b=1, f(n)= n(n-1) entonces k=2;
  Como a=1, T(n) = O(n ^k+1 ) 
  T(n)= O(n ²⁺¹ ) 
  T(n)= O(n ³ ) 
   
• Ejemplo-3 : 
  T(n) = 2T(n-1) – 1, si n>0 
       = 1, si n<=0
  Sol: Esta recurrencia no se puede resolver usando el método anterior 
  ya que la función no tiene la forma T( n) = aT(nb) + f(n) 
   

Este artículo es una contribución de Yash Singla . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a contribuido@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.