Calcular el número de Nodes en todos los subárboles | Uso de DFS

Dado un árbol en forma de lista de adyacencia, tenemos que calcular la cantidad de Nodes en el subárbol de cada Node mientras calculamos la cantidad de Nodes en el subárbol de un Node en particular, ese Node también se agregará como un Node en el subárbol, por lo tanto, el número de Nodes en el subárbol de hojas es 1. 

Ejemplos: 

Input : Consider the Graph mentioned below:

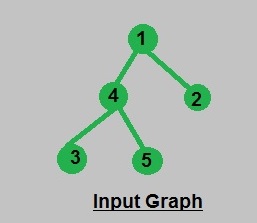
Output : Nodes in subtree of 1 : 5
         Nodes in subtree of 2 : 1
         Nodes in subtree of 3 : 1
         Nodes in subtree of 4 : 3
         Nodes in subtree of 5 : 1

Input : Consider the Graph mentioned below:

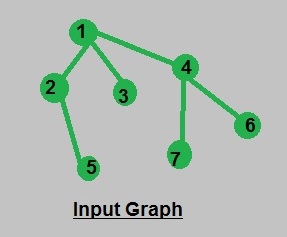
Output : Nodes in subtree of 1 : 7
         Nodes in subtree of 2 : 2
         Nodes in subtree of 3 : 1
         Nodes in subtree of 4 : 3
         Nodes in subtree of 5 : 1
         Nodes in subtree of 6 : 1
         Nodes in subtree of 7 : 1

Explicación: Primero debemos calcular el recuento de valores [s]: el número de Nodes en el subárbol de Nodes s. Donde subárbol contiene el propio Node y todos los Nodes del subárbol de sus hijos. Por lo tanto, podemos calcular el número de Nodes de forma recursiva utilizando el concepto de DFS y DP, donde debemos procesar cada borde solo una vez y contar [] el valor de los niños utilizados para calcular el recuento [] de su padre expresando el concepto de DP (programación dinámica ). 

Complejidad de tiempo: O(n) [en el procesamiento de todos los bordes (n-1)].

Algoritmo:

void numberOfNodes(int s, int e)
{
    vector::iterator u;
    cuenta1[s] = 1;
    for (u = adj[s].begin(); u != adj[s].end(); u++)
    {
        // condición para omitir la ruta inversa
        // ruta de los hijos a los padres 

        si (*u == e)
            continuar;
        // llamada recursiva para DFS

        numeroDeNodes(*u, s);

        // actualiza el valor de cuenta[] del padre usando
        // sus hijos

        cuenta1[s] += cuenta1[*u];
    }}

Implementación:

// CPP code to find number of nodes
// in subtree of each node
#include <bits/stdc++.h>
using namespace std;
 
const int N = 8;
 
// variables used to store data globally
int count1[N];
 
// adjacency list representation of tree
vector<int> adj[N];
 
// function to calculate no. of nodes in a subtree
void numberOfNodes(int s, int e)
{
    vector<int>::iterator u;
    count1[s] = 1;
    for (u = adj[s].begin(); u != adj[s].end(); u++) {
         
        // condition to omit reverse path
        // path from children to parent
        if (*u == e)
            continue;
         
        // recursive call for DFS
        numberOfNodes(*u, s);
         
        // update count[] value of parent using
        // its children
        count1[s] += count1[*u];
    }
}
 
// function to add edges in graph
void addEdge(int a, int b)
{
    adj[a].push_back(b);
    adj[b].push_back(a);
}
 
// function to print result
void printNumberOfNodes()
{
    for (int i = 1; i < N; i++) {
        cout << "\nNodes in subtree of " << i;
        cout << ": " << count1[i];
    }
}
 
// driver function
int main()
{
    // insertion of nodes in graph
    addEdge(1, 2);
    addEdge(1, 4);
    addEdge(1, 5);
    addEdge(2, 6);
    addEdge(4, 3);
    addEdge(4, 7);
     
    // call to perform dfs calculation
    // making 1  as root of tree
    numberOfNodes(1, 0);
     
    // print result
    printNumberOfNodes();
    return 0;
}

// A Java code to find number of nodes
// in subtree of each node
import java.util.ArrayList;
 
public class NodesInSubtree
{
    // variables used to store data globally
    static final int N = 8;
    static int count1[] = new int[N];
     
    // adjacency list representation of tree
    static ArrayList<Integer> adj[] = new ArrayList[N];
     
    // function to calculate no. of nodes in a subtree
    static void numberOfNodes(int s, int e)
    {
        count1[s] = 1;
        for(Integer u: adj[s])
        {
            // condition to omit reverse path
            // path from children to parent
            if(u == e)
                continue;
             
            // recursive call for DFS
            numberOfNodes(u ,s);
             
            // update count[] value of parent using
            // its children
            count1[s] += count1[u];
        }
    }
     
    // function to add edges in graph
    static void addEdge(int a, int b)
    {
        adj[a].add(b);
        adj[b].add(a);
    }
     
    // function to print result
    static void printNumberOfNodes()
    {
        for (int i = 1; i < N; i++)
            System.out.println("Node of a subtree of "+ i+
                                       " : "+ count1[i]);
    }
     
    // Driver function
    public static void main(String[] args)
    {
        // Creating list for all nodes
        for(int i = 0; i < N; i++)
            adj[i] = new ArrayList<>();
             
        // insertion of nodes in graph
        addEdge(1, 2);
        addEdge(1, 4);
        addEdge(1, 5);
        addEdge(2, 6);
        addEdge(4, 3);
        addEdge(4, 7);
         
        // call to perform dfs calculation
        // making 1  as root of tree
        numberOfNodes(1, 0);
         
        // print result
        printNumberOfNodes();
             
    }
 
}
// This code is contributed by Sumit Ghosh

# Python3 code to find the number of
# nodes in the subtree of each node
N = 8
 
# variables used to store data globally
count1 = [0] * (N)
 
# Adjacency list representation of tree
adj = [[] for i in range(N)]
 
# Function to calculate no. of
# nodes in subtree
def numberOfNodes(s, e):
 
    count1[s] = 1
    for u in adj[s]:
         
        # Condition to omit reverse path
        # path from children to parent
        if u == e:
            continue
         
        # recursive call for DFS
        numberOfNodes(u, s)
         
        # update count[] value of parent
        # using its children
        count1[s] += count1[u]
 
# Function to add edges in graph
def addEdge(a, b):
 
    adj[a].append(b)
    adj[b].append(a)
 
# Function to print result
def printNumberOfNodes():
 
    for i in range(1, N):
        print("Nodes in subtree of", i,
                        ":", count1[i])
 
# Driver Code
if __name__ == "__main__":
 
    # insertion of nodes in graph
    addEdge(1, 2)
    addEdge(1, 4)
    addEdge(1, 5)
    addEdge(2, 6)
    addEdge(4, 3)
    addEdge(4, 7)
     
    # call to perform dfs calculation
    # making 1 as root of tree
    numberOfNodes(1, 0)
     
    # print result
    printNumberOfNodes()
     
# This code is contributed by Rituraj Jain

// C# code to find number of nodes
// in subtree of each node
using System;
using System.Collections.Generic;
class GFG
{
    // variables used to store data globally
    static readonly int N = 8;
    static int []count1 = new int[N];
     
    // adjacency list representation of tree
    static List<int> []adj = new List<int>[N];
     
    // function to calculate no. of nodes in a subtree
    static void numberOfNodes(int s, int e)
    {
        count1[s] = 1;
        foreach(int u in adj[s])
        {
            // condition to omit reverse path
            // path from children to parent
            if(u == e)
                continue;
             
            // recursive call for DFS
            numberOfNodes(u, s);
             
            // update count[] value of parent using
            // its children
            count1[s] += count1[u];
        }
    }
     
    // function to add edges in graph
    static void addEdge(int a, int b)
    {
        adj[a].Add(b);
        adj[b].Add(a);
    }
     
    // function to print result
    static void printNumberOfNodes()
    {
        for (int i = 1; i < N; i++)
            Console.WriteLine("Node of a subtree of "+ i +
                                        " : "+ count1[i]);
    }
     
    // Driver Code
    public static void Main(String[] args)
    {
        // Creating list for all nodes
        for(int i = 0; i < N; i++)
            adj[i] = new List<int>();
             
        // insertion of nodes in graph
        addEdge(1, 2);
        addEdge(1, 4);
        addEdge(1, 5);
        addEdge(2, 6);
        addEdge(4, 3);
        addEdge(4, 7);
         
        // call to perform dfs calculation
        // making 1 as root of tree
        numberOfNodes(1, 0);
         
        // print result
        printNumberOfNodes();
    }
}
 
// This code is contributed by PrinciRaj1992

<script>
    // A Javascript code to find number of nodes
    // in subtree of each node
     
    // variables used to store data globally
    let N = 8;
    let count1 = new Array(N);
       
    // adjacency list representation of tree
    let adj = new Array(N);
       
    // function to calculate no. of nodes in a subtree
    function numberOfNodes(s, e)
    {
        count1[s] = 1;
        for(let u = 0; u < adj[s].length; u++)
        {
            // condition to omit reverse path
            // path from children to parent
            if(adj[s][u] == e)
                continue;
               
            // recursive call for DFS
            numberOfNodes(adj[s][u] ,s);
               
            // update count[] value of parent using
            // its children
            count1[s] += count1[adj[s][u]];
        }
    }
       
    // function to add edges in graph
    function addEdge(a, b)
    {
        adj[a].push(b);
        adj[b].push(a);
    }
       
    // function to print result
    function printNumberOfNodes()
    {
        for (let i = 1; i < N; i++)
            document.write("Node of a subtree of "+ i+
                                       " : "+ count1[i] + "</br>");
    }
     
    // Creating list for all nodes
    for(let i = 0; i < N; i++)
      adj[i] = [];
 
    // insertion of nodes in graph
    addEdge(1, 2);
    addEdge(1, 4);
    addEdge(1, 5);
    addEdge(2, 6);
    addEdge(4, 3);
    addEdge(4, 7);
 
    // call to perform dfs calculation
    // making 1  as root of tree
    numberOfNodes(1, 0);
 
    // print result
    printNumberOfNodes();
     
    // This code is contributed by suresh07.
</script>

Nodes in subtree of 1: 7
Nodes in subtree of 2: 2
Nodes in subtree of 3: 1
Nodes in subtree of 4: 3
Nodes in subtree of 5: 1
Nodes in subtree of 6: 1
Nodes in subtree of 7: 1

Ilustración de entrada y salida: 

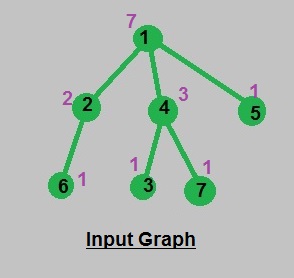
Este artículo es una contribución de Shivam Pradhan (anuj_charm) . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.