Dada una string, genere todas las permutaciones que no contengan ‘B’ después de ‘A’, es decir, la string no debe contener «AB» como una substring.
Ejemplos:
Entrada: str = “ABC”
Salida: ACB, BAC, BCA, CBA
De 6 permutaciones de “ABC”, 4 siguen la restricción dada y 2 (“ABC” y “CAB”) no la siguen.Entrada: str = “BCD”
Salida: BCD, BDC, CDB, CBD, DCB, DBC
Una solución simple es generar todas las permutaciones . Para cada permutación, verifique si sigue la restricción dada.
C++
// Simple C++ program to print all permutations
// of a string that follow given constraint
#include <bits/stdc++.h>
using namespace std;
void permute(string& str, int l, int r)
{
// Check if current permutation is
// valid
if (l == r) {
if (str.find("AB") == string::npos)
cout << str << " ";
return;
}
// Recursively generate all permutation
for (int i = l; i <= r; i++) {
swap(str[l], str[i]);
permute(str, l + 1, r);
swap(str[l], str[i]);
}
}
// Driver Code
int main()
{
string str = "ABC";
permute(str, 0, str.length() - 1);
return 0;
}
Java
// Simple Java program to print all
// permutations of a String that
// follow given constraint
import java.util.*;
class GFG{
static void permute(char[] str, int l, int r)
{
// Check if current permutation is
// valid
if (l == r)
{
if (!String.valueOf(str).contains("AB"))
System.out.print(String.valueOf(str) + " ");
return;
}
// Recursively generate all permutation
for(int i = l; i <= r; i++)
{
char tmp = str[l];
str[l] = str[i];
str[i] = tmp;
permute(str, l + 1, r);
tmp = str[l];
str[l] = str[i];
str[i] = tmp;
}
}
// Driver Code
public static void main(String[] args)
{
String str = "ABC";
permute(str.toCharArray(), 0,
str.length() - 1);
}
}
// This code is contributed by Amit Katiyar
Python
# Simple Python program to print all permutations
# of a string that follow given constraint
def permute(str, l, r):
# Check if current permutation is
# valid
if (l == r):
if "AB" not in ''.join(str):
print(''.join(str), end=" ")
return
# Recursively generate all permutation
for i in range(l, r + 1):
str[l], str[i] = str[i], str[l]
permute(str, l + 1, r)
str[l], str[i] = str[i], str[l]
# Driver Code
str = "ABC"
permute(list(str), 0, len(str) - 1)
# This code is contributed by SHUBHAMSINGH10
C#
// Simple C# program to print all permutations
// of a string that follow given constraint
using System;
using System.Text;
class GFG {
static void permute(StringBuilder str, int l, int r)
{
// Check if current permutation is
// valid
if (l == r) {
if (str.ToString().IndexOf("AB") == -1) {
Console.Write(str.ToString() + " ");
}
return;
}
// Recursively generate all permutation
for (int i = l; i <= r; i++) {
char tmp = str[l];
str[l] = str[i];
str[i] = tmp;
permute(str, l + 1, r);
tmp = str[l];
str[l] = str[i];
str[i] = tmp;
}
}
// Driver code
static void Main(string[] arg)
{
string str = "ABC";
StringBuilder s = new StringBuilder(str);
permute(s, 0, str.Length - 1);
}
}
// This code is contributed by rutvik_56
Javascript
<script>
// JavaScript code to implement the above approach
function permute(str, l, r)
{
// Check if current permutation is
// valid
if (l == r) {
if (str.indexOf("AB") == -1)
document.write(str," ");
return;
}
// Recursively generate all permutation
for (let i = l; i <= r; i++) {
let a = str.split("");
let temp = a[l];
a[l] = a[i];
a[i] = temp;
permute(a.join(""), l + 1, r);
temp = a[l];
a[l] = a[i];
a[i] = temp;
}
}
// Driver Code
let str = "ABC";
permute(str, 0, str.length - 1);
// This code is contributed by shinjanpatra
</script>
ACB BAC BCA CBA
La solución anterior primero genera todas las permutaciones, luego, para cada permutación, verifica si sigue la restricción dada o no.
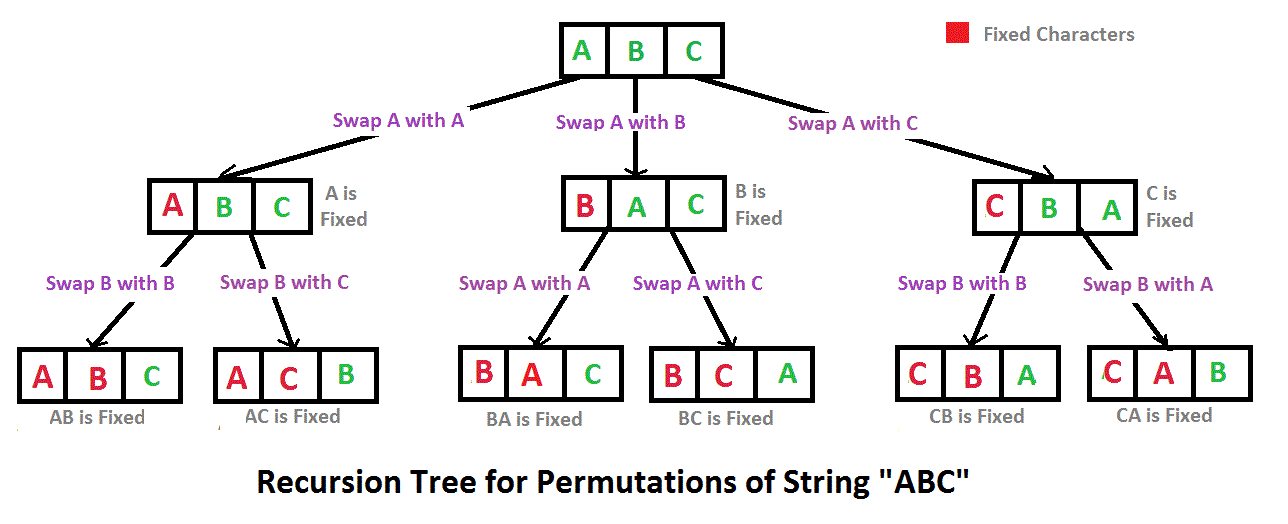
Una solución eficiente es utilizar Backtracking . Cortamos el árbol de recurrencia cada vez que vemos que se forma la substring «AB». Cómo hacemos esto? agregamos una función isSafe(). Antes de hacer un intercambio, verificamos si el carácter anterior es ‘A’ y el carácter actual es ‘B’.
A continuación se muestra la implementación del código anterior:
C++
// Backtracking based CPP program to print all
// permutations of a string that follow given
// constraint
#include <bits/stdc++.h>
using namespace std;
bool isSafe(string& str, int l, int i, int r)
{
// If previous character was 'A' and character
// is 'B', then do not proceed and cut down
// the recursion tree.
if (l != 0 && str[l - 1] == 'A' && str[i] == 'B')
return false;
// This condition is explicitly required for
// cases when last two characters are "BA". We
// do not want them to swapped and become "AB"
if (r == l + 1 && str[i] == 'A' && str[l] == 'B'
|| r == l + 1 && l == i && str[r] == 'B'
&& str[l] == 'A')
return false;
return true;
}
void permute(string& str, int l, int r)
{
// We reach here only when permutation
// is valid
if (l == r) {
cout << str << " ";
return;
}
// Fix all characters one by one
for (int i = l; i <= r; i++) {
// Fix str[i] only if it is a
// valid move.
if (isSafe(str, l, i, r)) {
swap(str[l], str[i]);
permute(str, l + 1, r);
swap(str[l], str[i]);
}
}
}
// Driver Code
int main()
{
string str = "ABC";
// Function call
permute(str, 0, str.length() - 1);
return 0;
}
Java
// Backtracking based JAVA program
// to print all permutations of a
// string that follow given constraint
public class GFG
{
public boolean isSafe(String str,
int l,
int i,
int r)
{
// If previous character was 'A'
// and character is 'B', then
// do not proceed and cut down the
// recursion tree.
if (l != 0 && str.charAt(l - 1) == 'A'
&& str.charAt(i) == 'B')
return false;
// This condition is explicitly required
// for cases when last two characters
// are "BA". We do not want them to
// swapped and become "AB"
if (r == l + 1 && str.charAt(i) == 'A'
&& str.charAt(l) == 'B'
|| r == l + 1 && l == i
&& str.charAt(r) == 'B'
&& str.charAt(l) == 'A')
return false;
return true;
}
/**
* permutation function
* @param str string to calculate
permutation for
* @param l starting index
* @param r end index
*/
private void permute(String str,
int l, int r)
{
// We reach here only when permutation
// is valid
if (l == r)
System.out.print(str + " ");
else
{
// Fix all characters one by one
for (int i = l; i <= r; i++)
{
// Fix str[i] only if it is a
// valid move.
if (isSafe(str, l, i, r))
{
str = swap(str, l, i);
permute(str, l + 1, r);
str = swap(str, l, i);
}
}
}
}
/**
* Swap Characters at position
* @param a string value
* @param i position 1
* @param j position 2
* @return swapped string
*/
public String swap(String a, int i, int j)
{
char temp;
char[] charArray = a.toCharArray();
temp = charArray[i];
charArray[i] = charArray[j];
charArray[j] = temp;
return String.valueOf(charArray);
}
// Driver Code
public static void main(String[] args)
{
String str = "ABC";
int n = str.length();
GFG permutation = new GFG();
// Function call
permutation.permute(str, 0, n - 1);
}
}
Python
# Backtracking based Python3 program to print all # permutations of a string that follow given # constraint def isSafe(str, l, i, r): # If previous character was 'A' and character # is 'B', then do not proceed and cut down # the recursion tree. if (l != 0 and str[l - 1] == 'A' and str[i] == 'B'): return False # This condition is explicitly required for # cases when last two characters are "BA". We # do not want them to swapped and become "AB" if (r == l + 1 and str[i] == 'A' and str[l] == 'B' or r == l + 1 and l == i and str[r] == 'B' and str[l] == 'A'): return False return True def permute(str, l, r): # We reach here only when permutation # is valid if (l == r): print(*str, sep="", end=" ") return # Fix all characters one by one for i in range(l, r + 1): # Fix str[i] only if it is a # valid move. if (isSafe(str, l, i, r)): str[l], str[i] = str[i], str[l] permute(str, l + 1, r) str[l], str[i] = str[i], str[l] # Driver Code str = "ABC" # Function call permute(list(str), 0, len(str) - 1) # This code is contributed by SHUBHAMSINGH10
C#
// Backtracking based C# program to print all
// permutations of a string that follow given
// constraint
using System;
public class GFG
{
// Backtracking based C# program
// to print all permutations of a
// string that follow given constraint
using System;
using System.Text;
class GFG {
static bool isSafe(StringBuilder str,
int l, int i,
int r)
{
// If previous character was 'A'
// and character is 'B', then do not
// proceed and cut down the recursion tree.
if (l != 0 && str[l - 1] == 'A'
&& str[i] == 'B')
return false;
// This condition is explicitly
// required for cases when last two
// characters are "BA". We do not want
// them to swapped and become "AB"
if (r == l + 1 && str[i] == 'A'
&& str[l] == 'B' || r == l + 1
&& l == i && str[r] == 'B'
&& str[l] == 'A')
return false;
return true;
}
static void permute(StringBuilder str,
int l, int r)
{
// We reach here only when permutation
// is valid
if (l == r)
{
Console.Write(str + " ");
return;
}
// Fix all characters one by one
for (int i = l; i <= r; i++)
{
// Fix str[i] only if it is a
// valid move.
if (isSafe(str, l, i, r))
{
char temp = str[l];
str[l] = str[i];
str[i] = temp;
permute(str, l + 1, r);
temp = str[l];
str[l] = str[i];
str[i] = temp;
}
}
}
// Driver code
static void Main()
{
string str = "ABC";
StringBuilder s = new StringBuilder(str);
// Function call
permute(s, 0, str.Length - 1);
}
}
// This code is contributed by divyeshrabadiya07
ACB BAC BCA CBA