Hay cinco hojas de papel, cada una de las cuales tiene un número entero en un lado y un alfabeto en el otro lado escrito como se muestra a continuación.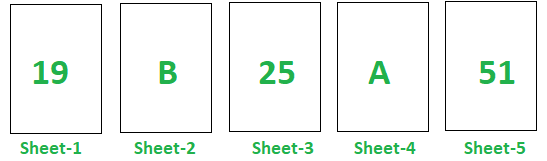
¿Cuál es el número mínimo de hojas necesarias y suficientes que dará la vuelta para verificar si la proposición que se da a continuación sobre ellas es verdadera o falsa? ¿Cuáles son las hojas que vas a voltear?
Proposición: “Si hay un número primo en un lado de una hoja, entonces el otro lado de la hoja tiene una vocal”.
Respuesta: Dos: Hojas 1 y 2.
Solución: Hay que dar la vuelta a la hoja 1 para verificar la verdad de la proposición. Si no contiene una vocal en el otro lado, entonces la proposición puede declararse como falsa. Esto verificará que la afirmación sea verdadera. También hay que dar la vuelta a la hoja 2. Si tiene un número primo en el otro lado, refutará la proposición. Esto verificará que la declaración sea generalmente cierta para todos los casos con la ayuda de la contradicción. No es necesario voltear la hoja 4 porque la proposición no implica que solo aquellas hojas con un número primo en un lado tengan una vocal en el otro. Las hojas 3 y 5 no son de ayuda para refutar o probar la proposición obviamente.