Dado un árbol de N Nodes y N-1 aristas. También dado un entero M y un Node, la tarea es imprimir el M-ésimo Node en el DFS del subárbol de un Node determinado para consultas múltiples.
Nota : M no será mayor que el número de Nodes en el subárbol del Node dado.
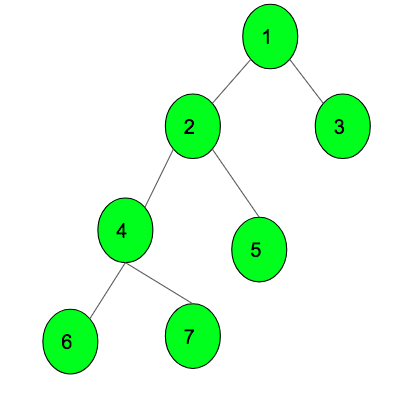
Entrada: M = 3, Node = 1
Salida: 4
En el ejemplo anterior, si se da 1 como Node, entonces el DFS del subárbol será 1 2 4 6 7 5 3 , por lo tanto, si M es 3, entonces el tercer Node es 4Entrada: M = 4, Node = 2
Salida: 7
Si se da 2 como Node, entonces el DFS del subárbol será 2 4 6 7 5. Por lo tanto, si M es 4, entonces el cuarto Node es 7.
Acercarse:
- Agregue los bordes entre los Nodes en una lista de adyacencia.
- Llame a la función DFS para generar el DFS del árbol completo.
- Use una array under[] para almacenar la altura del subárbol debajo del Node dado, incluido el Node.
- En la función DFS, siga incrementando el tamaño del subárbol en cada llamada recursiva.
- Marque el índice de Node en el DFS de completo usando hashing.
- Sea ind el índice del Node dado en el DFS del árbol , entonces el M-ésimo Node estará en el índice ind + M -1 ya que el DFS de un subárbol de un Node siempre será un subarreglo contiguo a partir del Node.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program for Queries
// for DFS of subtree of a node in a tree
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
// Adjacency list to store the
// tree nodes connection
vector<int> v[N];
// stores the index of node in DFS
unordered_map<int, int> mp;
// stores the index of node in
// original node
vector<int> a;
// Function to call DFS and count nodes
// under that subtree
void dfs(int under[], int child, int parent)
{
// stores the DFS of tree
a.push_back(child);
// height of subtree
under[child] = 1;
// iterate for children
for (auto it : v[child]) {
// if not equal to parent
// so that it does not traverse back
if (it != parent) {
// call DFS for subtree
dfs(under, it, child);
// add the height
under[child] += under[it];
}
}
}
// Function to return the DFS of subtree of node
int printnodeDFSofSubtree(int node, int under[], int m)
{
// index of node in the original DFS
int ind = mp[node];
// height of subtree of node
return a[ind + m - 1];
}
// Function to add edges to a tree
void addEdge(int x, int y)
{
v[x].push_back(y);
v[y].push_back(x);
}
// Marks the index of node in original DFS
void markIndexDfs()
{
int size = a.size();
// marks the index
for (int i = 0; i < size; i++) {
mp[a[i]] = i;
}
}
// Driver Code
int main()
{
int n = 7;
// add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// array to store the height of subtree
// of every node in a tree
int under[n + 1];
// Call the function DFS to generate the DFS
dfs(under, 1, 0);
// Function call to mark the index of node
markIndexDfs();
int m = 3;
// Query 1
cout << printnodeDFSofSubtree(1, under, m) << endl;
// Query 2
m = 4;
cout << printnodeDFSofSubtree(2, under, m);
return 0;
}
Java
// Java program for Queries for
// DFS of subtree of a node in a tree
import java.util.*;
class GFG{
// Adjacency list to store the
// tree nodes connection
static ArrayList<ArrayList<Integer>> v;
// Stores the index of node in DFS
static HashMap<Integer, Integer> mp;
// Stores the index of node in
// original node
static ArrayList<Integer> a;
// Function to call DFS and count nodes
// under that subtree
static void dfs(int under[], int child,
int parent)
{
// Stores the DFS of tree
a.add(child);
// Height of subtree
under[child] = 1;
// iterate for children
for(int it : v.get(child))
{
// If not equal to parent
// so that it does not traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// Add the height
under[child] += under[it];
}
}
}
// Function to return the DFS of subtree of node
static int printnodeDFSofSubtree(int node,
int under[],
int m)
{
// Index of node in the original DFS
int ind = mp.get(node);
// Height of subtree of node
return a.get(ind + m - 1);
}
// Function to add edges to a tree
static void addEdge(int x, int y)
{
v.get(x).add(y);
v.get(y).add(x);
}
// Marks the index of node in original DFS
static void markIndexDfs()
{
int size = a.size();
// Marks the index
for(int i = 0; i < size; i++)
{
mp.put(a.get(i), i);
}
}
// Driver Code
public static void main(String[] args)
{
int n = 7;
mp = new HashMap<>();
v = new ArrayList<>();
a = new ArrayList<>();
for(int i = 0; i < n + 1; i++)
v.add(new ArrayList<>());
// Add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height of subtree
// of every node in a tree
int under[] = new int[n + 1];
// Call the function DFS to generate the DFS
dfs(under, 1, 0);
// Function call to mark the index of node
markIndexDfs();
int m = 3;
// Query 1
System.out.println(
printnodeDFSofSubtree(1, under, m));
// Query 2
m = 4;
System.out.println(
printnodeDFSofSubtree(2, under, m));
}
}
// This code is contributed by jrishabh99
Python3
# Python3 program for Queries
# for DFS of subtree of a node in a tree
N = 100000
# Adjacency list to store the
# tree nodes connection
v = [[]for i in range(N)]
# stores the index of node in DFS
mp = {}
# stores the index of node in
# original node
a = []
# Function to call DFS and count nodes
# under that subtree
def dfs(under, child, parent):
# stores the DFS of tree
a.append(child)
# height of subtree
under[child] = 1
# iterate for children
for it in v[child]:
# if not equal to parent
# so that it does not traverse back
if (it != parent):
# call DFS for subtree
dfs(under, it, child)
# add the height
under[child] += under[it]
# Function to return the DFS of subtree of node
def printnodeDFSofSubtree(node, under, m):
# index of node in the original DFS
ind = mp[node]
# height of subtree of node
return a[ind + m - 1]
# Function to add edges to a tree
def addEdge(x, y):
v[x].append(y)
v[y].append(x)
# Marks the index of node in original DFS
def markIndexDfs():
size = len(a)
# marks the index
for i in range(size):
mp[a[i]] = i
# Driver Code
n = 7
# add edges of a tree
addEdge(1, 2)
addEdge(1, 3)
addEdge(2, 4)
addEdge(2, 5)
addEdge(4, 6)
addEdge(4, 7)
# array to store the height of subtree
# of every node in a tree
under = [0]*(n + 1)
# Call the function DFS to generate the DFS
dfs(under, 1, 0)
# Function call to mark the index of node
markIndexDfs()
m = 3
# Query 1
print(printnodeDFSofSubtree(1, under, m))
# Query 2
m = 4
print(printnodeDFSofSubtree(2, under, m))
# This code is contributed by SHUBHAMSINGH10
C#
// C# program for Queries for DFS
// of subtree of a node in a tree
using System;
using System.Collections.Generic;
class GFG{
// Adjacency list to store the
// tree nodes connection
static List<List<int>> v;
// Stores the index of node in DFS
static Dictionary<int, int> mp;
// Stores the index of node in
// original node
static List<int> a;
// Function to call DFS and count nodes
// under that subtree
static void dfs(int []under, int child,
int parent)
{
// Stores the DFS of tree
a.Add(child);
// Height of subtree
under[child] = 1;
// Iterate for children
foreach(int it in v[child])
{
// If not equal to parent so
// that it does not traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// Add the height
under[child] += under[it];
}
}
}
// Function to return the DFS of subtree of node
static int printnodeDFSofSubtree(int node,
int []under,
int m)
{
// Index of node in the original DFS
int ind = mp[node];
// Height of subtree of node
return a[ind + m - 1];
}
// Function to add edges to a tree
static void addEdge(int x, int y)
{
v[x].Add(y);
v[y].Add(x);
}
// Marks the index of node in original DFS
static void markIndexDfs()
{
int size = a.Count;
// Marks the index
for(int i = 0; i < size; i++)
{
mp.Add(a[i], i);
}
}
// Driver Code
public static void Main(String[] args)
{
int n = 7;
mp = new Dictionary<int, int>();
v = new List<List<int>>();
a = new List<int>();
for(int i = 0; i < n + 1; i++)
v.Add(new List<int>());
// Add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height of subtree
// of every node in a tree
int []under = new int[n + 1];
// Call the function DFS to generate the DFS
dfs(under, 1, 0);
// Function call to mark the index of node
markIndexDfs();
int m = 3;
// Query 1
Console.WriteLine(
printnodeDFSofSubtree(1, under, m));
// Query 2
m = 4;
Console.WriteLine(
printnodeDFSofSubtree(2, under, m));
}
}
// This code is contributed by Amit Katiyar
Javascript
<script>
// Javascript program for Queries for DFS
// of subtree of a node in a tree
// Adjacency list to store the
// tree nodes connection
var v = [];
// Stores the index of node in DFS
var mp = new Map();
// Stores the index of node in
// original node
var a = [];
// Function to call DFS and count nodes
// under that subtree
function dfs(under, child, parent)
{
// Stores the DFS of tree
a.push(child);
// Height of subtree
under[child] = 1;
// Iterate for children
for(var it of v[child])
{
// If not equal to parent so
// that it does not traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// Push the height
under[child] += under[it];
}
}
}
// Function to return the DFS of subtree of node
function printnodeDFSofSubtree(node, under, m)
{
// Index of node in the original DFS
var ind = mp.get(node);
// Height of subtree of node
return a[ind + m - 1];
}
// Function to add edges to a tree
function addEdge(x, y)
{
v[x].push(y);
v[y].push(x);
}
// Marks the index of node in original DFS
function markIndexDfs()
{
var size = a.length;
// Marks the index
for(var i = 0; i < size; i++)
{
mp.set(a[i], i);
}
}
// Driver Code
var n = 7;
mp = new Map();
v = [];
a = [];
for(var i = 0; i < n + 1; i++)
v.push(Array());
// Push edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height of subtree
// of every node in a tree
var under = new Array(n + 1);
// Call the function DFS to generate the DFS
dfs(under, 1, 0);
// Function call to mark the index of node
markIndexDfs();
var m = 3;
// Query 1
document.write(printnodeDFSofSubtree(
1, under, m) + "<br>");
// Query 2
m = 4;
document.write(printnodeDFSofSubtree(
2, under, m));
// This code is contributed by rutvik_56
</script>
Producción:
4 7
Complejidad Temporal: O(1), para el procesamiento de cada consulta.
Espacio Auxiliar: O(N)