Dados tres números (x, y y z) que denotan el número de personas en el primer grupo, el segundo grupo y el tercer grupo. Podemos formar grupos seleccionando personas del primer grupo, del segundo grupo y del tercer grupo de manera que las siguientes condiciones no sean nulas.
- Se debe seleccionar un mínimo de una persona de cada grupo.
- El número de personas seleccionadas del primer grupo tiene que ser al menos uno más que el número de personas seleccionadas del tercer grupo.
La tarea es encontrar el número de formas de formar grupos distintos.
Ejemplos:
Entrada: x = 3, y = 2, z = 1
Salida: 9
Digamos que x tiene personas (a, b, c)
Y tiene personas (d, e)
Z tiene personas (f)
Entonces las 9 formas son {a, b, d, f}, {a, b, e, f}, {a, c, d, f}, {a, c, e, f}, {b, c, d, f}, {b
, c, e, f}, {a, b, c, d, f}, {a, b, c, e, f} y {a, b, c, d, e, f} Entrada: x
=
4 , y = 2, z = 1
Salida: 27
El problema se puede resolver usando combinatoria . Hay tres puestos (en términos de personas de diferentes grupos) que deben cubrirse. El primero tiene que ser llenado con un número con uno o más que la segunda posición. El tercero se puede llenar con cualquier número. Sabemos que si necesitamos cubrir k puestos con N personas, entonces el número de formas de hacerlo es ![]() . Por lo tanto, se pueden seguir los siguientes pasos para resolver el problema anterior.
. Por lo tanto, se pueden seguir los siguientes pasos para resolver el problema anterior.
- La segunda posición se puede llenar con i = 1 a i = y personas.
- La primera posición se puede llenar con j = i+1 a j = x personas.
- El tercer puesto puede ocuparse con cualquier número de k = 1 a k = z personas.
- De ahí que lo común sea ocupar el tercer puesto con k personas. Por lo tanto, podemos tomar esa porción como común.
- Ejecute dos bucles (i y j) para llenar la segunda posición y la primera posición respectivamente.
- El número de formas de cubrir las posiciones es
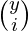 *
* 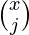 .
. - Después del cálculo de todas las formas de llenar esas dos posiciones, simplemente podemos multiplicar la suma de
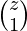 ++
++ 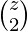 …
…  ya que esa era la parte común en ambos.
ya que esa era la parte común en ambos.
![]() can be pre-computed using Dynamic Programming to reduce time complexity. The method is discussed here.
can be pre-computed using Dynamic Programming to reduce time complexity. The method is discussed here.
Below is the implementation of the above approach.
C++
// C++ program to find the number of
// ways to form the group of people
#include <bits/stdc++.h>
using namespace std;
int C[1000][1000];
// Function to pre-compute the
// Combination using DP
void binomialCoeff(int n)
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++) {
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
// return C[n][k];
}
// Function to find the number of ways
int numberOfWays(int x, int y, int z)
{
// Function to pre-compute
binomialCoeff(max(x, max(y, z)));
// Sum the Zci
int sum = 0;
for (int i = 1; i <= z; i++) {
sum = (sum + C[z][i]);
}
// Iterate for second position
int sum1 = 0;
for (int i = 1; i <= y; i++) {
// Iterate for first position
for (int j = i + 1; j <= x; j++) {
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
// Multiply the common Combination value
sum1 = (sum * sum1);
return sum1;
}
// Driver Code
int main()
{
int x = 3;
int y = 2;
int z = 1;
cout << numberOfWays(x, y, z);
return 0;
}
Java
// Java program to find the number of
// ways to form the group of peopls
class GFG
{
static int C[][] = new int [1000][1000];
// Function to pre-compute the
// Combination using DP
static void binomialCoeff(int n)
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++)
{
for (j = 0; j <= i; j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
// return C[n][k];
}
// Function to find the number of ways
static int numberOfWays(int x, int y, int z)
{
// Function to pre-compute
binomialCoeff(Math.max(x, Math.max(y, z)));
// Sum the Zci
int sum = 0;
for (int i = 1; i <= z; i++)
{
sum = (sum + C[z][i]);
}
// Iterate for second position
int sum1 = 0;
for (int i = 1; i <= y; i++)
{
// Iterate for first position
for (int j = i + 1; j <= x; j++)
{
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
// Multiply the common Combination value
sum1 = (sum * sum1);
return sum1;
}
// Driver Code
public static void main(String args[])
{
int x = 3;
int y = 2;
int z = 1;
System.out.println(numberOfWays(x, y, z));
}
}
// This code is contributed by Arnab Kundu
Python3
# Python3 program to find the number of # ways to form the group of peopls C = [[0 for i in range(1000)] for i in range(1000)] # Function to pre-compute the # Combination using DP def binomialCoeff(n): i, j = 0, 0 # Calculate value of Binomial Coefficient # in bottom up manner for i in range(n + 1): for j in range(i + 1): # Base Cases if (j == 0 or j == i): C[i][j] = 1 # Calculate value using previously # stored values else: C[i][j] = C[i - 1][j - 1] + \ C[i - 1][j] # return C[n][k] # Function to find the number of ways def numberOfWays(x, y, z): # Function to pre-compute binomialCoeff(max(x, max(y, z))) # Sum the Zci sum = 0 for i in range(1, z + 1): sum = (sum + C[z][i]) # Iterate for second position sum1 = 0 for i in range(1, y + 1): # Iterate for first position for j in range(i + 1, x + 1): sum1 = (sum1 + (C[y][i] * C[x][j])) # Multiply the common Combination value sum1 = (sum * sum1) return sum1 # Driver Code x = 3 y = 2 z = 1 print(numberOfWays(x, y, z)) # This code is contributed by Mohit Kumar
C#
// C# program to find the number of
// ways to form the group of peopls
using System;
class GFG
{
static int [,]C = new int [1000,1000];
// Function to pre-compute the
// Combination using DP
static void binomialCoeff(int n)
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++)
{
for (j = 0; j <= i; j++)
{
// Base Cases
if (j == 0 || j == i)
C[i,j] = 1;
// Calculate value using previously
// stored values
else
C[i,j] = C[i - 1,j - 1] + C[i - 1,j];
}
}
// return C[n,k];
}
// Function to find the number of ways
static int numberOfWays(int x, int y, int z)
{
// Function to pre-compute
binomialCoeff(Math.Max(x, Math.Max(y, z)));
// Sum the Zci
int sum = 0;
for (int i = 1; i <= z; i++)
{
sum = (sum + C[z,i]);
}
// Iterate for second position
int sum1 = 0;
for (int i = 1; i <= y; i++)
{
// Iterate for first position
for (int j = i + 1; j <= x; j++)
{
sum1 = (sum1 + (C[y,i] * C[x,j]));
}
}
// Multiply the common Combination value
sum1 = (sum * sum1);
return sum1;
}
// Driver Code
public static void Main(String []args)
{
int x = 3;
int y = 2;
int z = 1;
Console.WriteLine(numberOfWays(x, y, z));
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript program to find the number of
// ways to form the group of peopls
var C = Array(1000).fill().map(()=>Array(1000).fill(0));
// Function to pre-compute the
// Combination using DP
function binomialCoeff(n) {
var i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++) {
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
// return C[n][k];
}
// Function to find the number of ways
function numberOfWays(x , y , z) {
// Function to pre-compute
binomialCoeff(Math.max(x, Math.max(y, z)));
// Sum the Zci
var sum = 0;
for (i = 1; i <= z; i++) {
sum = (sum + C[z][i]);
}
// Iterate for second position
var sum1 = 0;
for (i = 1; i <= y; i++) {
// Iterate for first position
for (j = i + 1; j <= x; j++) {
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
// Multiply the common Combination value
sum1 = (sum * sum1);
return sum1;
}
// Driver Code
var x = 3;
var y = 2;
var z = 1;
document.write(numberOfWays(x, y, z));
// This code contributed by aashish1995
</script>
9
Complejidad temporal: O(K * K), donde K es el máximo de (x, y, z).
Espacio Auxiliar : O(1)