Dado un grafo no dirigido con vértices V y aristas E , la tarea es verificar si el componente conexo más grande del grafo forma un palíndromo en el grafo no dirigido.
Ejemplos:
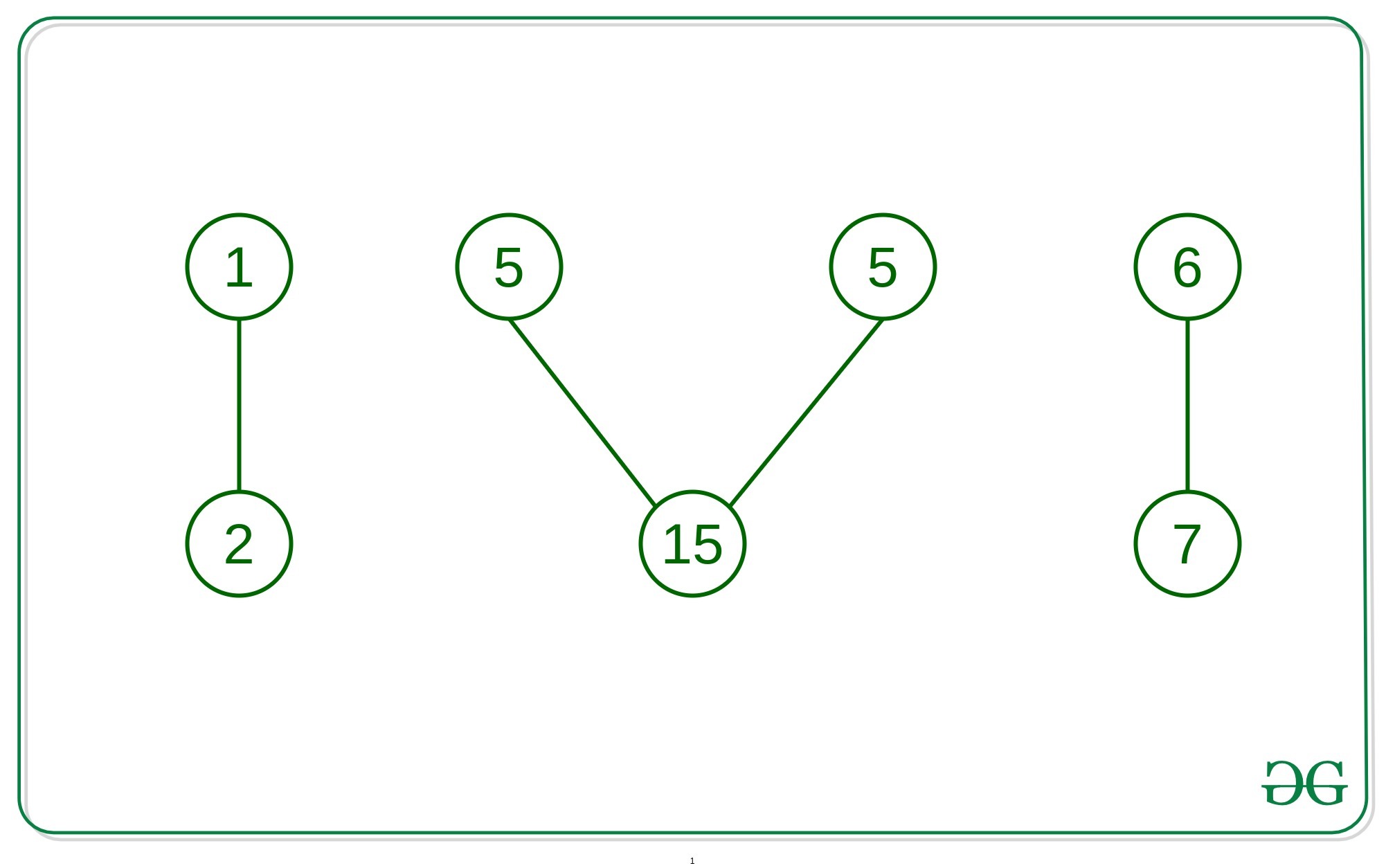
Aporte:
Salida:
el componente conexo más largo es el palíndromo.
Explicación:
el componente conexo más largo es {5, 15, 5},
que forma un palíndromo por valores.Aporte:
Salida:
el componente conectado más largo no es un palíndromo.
Explicación:
la string más larga es {2, 3, 4, 5}, que no es un palíndromo.
Enfoque: La idea es utilizar el recorrido de búsqueda primero en profundidad para realizar un seguimiento de los componentes conectados en el gráfico no dirigido. En cada recorrido, si la longitud actual del componente conectado es mayor que la longitud global del componente conectado, actualice el componente conectado más largo. Finalmente, verifique que el componente conectado más largo forme un palíndromo.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to check if
// longest connected component is
// palindrome in undirected graph
#include <bits/stdc++.h>
using namespace std;
// Function to traverse the undirected
// graph using the Depth first traversal
void depthFirst(int v, vector<int> graph[],
vector<bool>& visited,
vector<int>& storeChain)
{
// Marking the visited
// vertex as true
visited[v] = true;
// Store the connected chain
storeChain.push_back(v);
for (auto i : graph[v]) {
if (visited[i] == false) {
// Recursive call to
// the DFS algorithm
depthFirst(i, graph,
visited, storeChain);
}
}
}
// Function to check that the connected
// component forms a palindrome
void checkPalin(int arr[], int n)
{
// Container to store the frequency
// of each occurring element
map<int,int> frequency;
// Container to visit elements
unordered_set<int> element;
for(int i = 0; i < n; i ++)
{
// If element has not been visited already
// the element is inserted with freq = 1
// frequency of occurrence, if visited
// already, then frequency is updated
if(!(element.find(arr[i]) != element.end()))
{
frequency.insert({arr[i], 1});
}
else
{
frequency[arr[i]] ++;
}
element.insert(arr[i]);
}
// Variable to store final result
int result = 1;
// For even array size, all the elements
// are checked for even occurrences, if
// odd array size, then it is checked if
// a single element with odd frequency
// is present or not
if(n % 2 == 0)
{
for(auto i: frequency)
{
if(i.second % 2 != 0)
{
result = 0;
break;
}
}
}
else
{
int countFreq = 0;
for(auto i: frequency)
{
if(i.second % 2 != 0)
{
countFreq ++;
}
}
if(countFreq != 1)
result = 0;
}
// Printing the final result
if(result)
cout << "Longest connected component is Palindrome";
else
cout << "Longest connected component not a Palindrome";
}
// Function to check that longest connected
// component forms a palindrome
void longestConnectionPalin(
vector<int> graph[], int vertices,
vector<int> values)
{
// Initializing boolean array
// to mark visited vertices
vector<bool> visited(10001, false);
// maxChain stores the
// maximum chain size
int maxChain = 0;
// Container to store longest chain
vector<int> maxStoreChain;
// Following loop invokes DFS algorithm
for (int i = 1; i <= vertices; i++) {
if (visited[i] == false) {
// Variable to hold
// temporary length
int sizeChain;
// Container to store each chain
vector<int> storeChain;
// DFS algorithm
depthFirst(i, graph, visited, storeChain);
// Variable to hold each chain size
sizeChain = storeChain.size();
if (sizeChain > maxChain) {
maxChain = sizeChain;
maxStoreChain = storeChain;
}
}
}
// Container to store values
// of vertices of longest chain
int longChainValues[maxChain+1];
// Storing the values of longest chain
for(int i = 0; i < maxChain; i ++)
{
int temp = values[maxStoreChain[i]-1];
longChainValues[i] = temp;
}
// Function call to check for Palindrome
checkPalin(longChainValues, maxChain);
}
// Driver function to test above function
int main()
{
// Initializing graph in the form of adjacency list
vector<int> graph[1001];
// Defining the number of edges and vertices
int E, V;
E = 4;
V = 7;
// Assigning the values for each
// vertex of the undirected graph
vector<int> values;
values.push_back(10);
values.push_back(25);
values.push_back(5);
values.push_back(15);
values.push_back(5);
values.push_back(20);
values.push_back(0);
// Constructing the undirected graph
graph[1].push_back(2);
graph[2].push_back(1);
graph[3].push_back(4);
graph[4].push_back(3);
graph[3].push_back(5);
graph[5].push_back(3);
graph[6].push_back(7);
graph[7].push_back(6);
longestConnectionPalin(graph, V, values);
return 0;
}
Java
// Java implementation to check if
// longest connected component is
// palindrome in undirected graph
import java.util.*;
class GFG{
// Initializing boolean array
// to mark visited vertices
static boolean [] visited =
new boolean[10001];
// Container to store longest chain
static Vector<Integer>storeChain =
new Vector<>();
// Function to traverse
// the undirected graph
// using the Depth first
// traversal
static void depthFirst(int v,
Vector<Integer> graph[])
{
// Marking the visited
// vertex as true
visited[v] = true;
// Store the connected chain
storeChain.add(v);
for (int i : graph[v])
{
if (visited[i] == false)
{
// Recursive call to
// the DFS algorithm
depthFirst(i, graph);
}
}
}
// Function to check that
// the connected component
// forms a palindrome
static void checkPalin(int arr[],
int n)
{
// Container to store the
// frequency of each occurring
// element
HashMap<Integer,
Integer> frequency =
new HashMap<>();
// Container to visit elements
HashSet<Integer> element =
new HashSet<>();
for(int i = 0; i < n; i ++)
{
// If element has not been
// visited already the element
// is inserted with freq = 1
// frequency of occurrence,
// if visited already, then
// frequency is updated
if((element.contains(arr[i])))
{
frequency.put(arr[i],
frequency.get(arr[i]) + 1);
}
else
{
frequency.put(arr[i], 1);
}
element.add(arr[i]);
}
// Variable to store
// final result
int result = 1;
// For even array size, all
// the elements are checked
// for even occurrences, if
// odd array size, then it
// is checked if a single
// element with odd frequency
// is present or not
if(n % 2 == 0)
{
for (Map.Entry<Integer,
Integer> i : frequency.entrySet())
{
if(i.getValue() % 2 != 0)
{
result = 0;
break;
}
}
}
else
{
int countFreq = 0;
for (Map.Entry<Integer,
Integer> i : frequency.entrySet())
{
if(i.getValue() % 2 != 0)
{
countFreq ++;
}
}
if(countFreq != 1)
result = 0;
}
// Printing the
// final result
if(result != 0)
System.out.print("Longest connected " +
"component is Palindrome");
else
System.out.print("Longest connected " +
"component not a Palindrome");
}
// Function to check that longest
// connected component forms a palindrome
static void longestConnectionPalin(Vector<Integer> graph[],
int vertices,
Vector<Integer> values)
{
// maxChain stores the ;
// maximum chain size
int maxChain = 0;
// Container to store each chain
Vector<Integer> maxStoreChain =
new Vector<>();
// Following loop invokes
// DFS algorithm
for (int i = 1; i <= vertices; i++)
{
if (visited[i] == false)
{
// Variable to hold
// temporary length
int sizeChain;
// DFS algorithm
depthFirst(i, graph);
// Variable to hold each chain size
sizeChain = storeChain.size();
if (sizeChain > maxChain)
{
maxChain = sizeChain;
maxStoreChain = storeChain;
}
}
}
// Container to store values
// of vertices of longest chain
int []longChainValues =
new int[maxChain+1];
// Storing the values of
// longest chain
for(int i = 0; i < maxChain; i ++)
{
int temp = values.get(maxStoreChain.get(i) - 1);
longChainValues[i] = temp;
}
// Function call to check
// for Palindrome
checkPalin(longChainValues,
maxChain);
}
// Driver code
public static void main(String[] args)
{
// Initializing graph in the
// form of adjacency list
Vector<Integer> graph[] =
new Vector[1001];
for (int i = 0; i < graph.length; i++)
graph[i] = new Vector<Integer>();
// Defining the number of
// edges and vertices
int E, V;
E = 4;
V = 7;
// Assigning the values
// for each vertex of
// the undirected graph
Vector<Integer> values =
new Vector<>();
values.add(10);
values.add(25);
values.add(5);
values.add(15);
values.add(5);
values.add(20);
values.add(0);
// Constructing the
// undirected graph
graph[1].add(2);
graph[2].add(1);
graph[3].add(4);
graph[4].add(3);
graph[3].add(5);
graph[5].add(3);
graph[6].add(7);
graph[7].add(6);
longestConnectionPalin(graph, V, values);
}
}
// This code is contributed by gauravrajput1
Python3
# Python3 implementation to check if
# longest connected component is
# palindrome in undirected graph
# Function to traverse the undirected
# graph using the Depth first traversal
def depthFirst(v):
global graph, visited, storeChain
# Marking the visited
# vertex as true
visited[v] = True
# Store the connected chain
storeChain.append(v)
for i in graph[v]:
if (visited[i] == False):
# Recursive call to
# the DFS algorithm
depthFirst(i)
# Function to check that the connected
# component forms a palindrome
def checkPalin(arr, n):
# Container to store the frequency
# of each occurring element
frequency = {}
# Container to visit elements
element = {}
for i in range(n):
# If element has not been visited already
# the element is inserted with freq = 1
# frequency of occurrence, if visited
# already, then frequency is updated
if (arr[i] not in element):
frequency[arr[i]] = 1
else:
frequency[arr[i]] += 1
element[arr[i]] = 1
# Variable to store final result
result = 1
# For even array size, all the elements
# are checked for even occurrences, if
# odd array size, then it is checked if
# a single element with odd frequency
# is present or not
if (n % 2 == 0):
for i in frequency:
if (frequency[i] % 2 != 0):
result = 0
break
else:
countFreq = 0
for i in frequency:
if frequency[i] % 2 != 0:
countFreq += 1
if (countFreq != 1):
result = 0
# Printing the final result
if(not result):
print("Longest connected "
"component is Palindrome")
else:
print("Longest connected "
"component not a Palindrome")
# Function to check that longest connected
# component forms a palindrome
def longestConnectionPalin(vertices):
global visited, graph, storeChain, values
# maxChain stores the
# maximum chain size
maxChain = 0
# Container to store longest chain
maxStoreChain = []
# Following loop invokes DFS algorithm
for i in range(1, vertices + 1):
if (visited[i] == False):
# Variable to hold
# temporary length
sizeChain = 0
# DFS algorithm
depthFirst(i)
# Variable to hold each chain size
sizeChain = len(storeChain)
if (sizeChain > maxChain):
maxChain = sizeChain
maxStoreChain = storeChain
# Storing the values of longest chain
for i in range(maxChain):
temp = values[maxStoreChain[i] - 1]
longChainValues[i] = temp
# Function call to check for Palindrome
checkPalin(longChainValues, maxChain)
# Driver Code
if __name__ == '__main__':
# Initializing graph in the form
# of adjacency list
graph = [[] for i in range(10001)]
visited = [False for i in range(10001)]
storeChain = []
longChainValues = [0 for i in range(10001)]
# Defining the number of edges and vertices
E = 4
V = 7
# Assigning the values for each
# vertex of the undirected graph
values = []
values.append(10)
values.append(25)
values.append(5)
values.append(15)
values.append(5)
values.append(20)
values.append(0)
# Constructing the undirected graph
graph[1].append(2)
graph[2].append(1)
graph[3].append(4)
graph[4].append(3)
graph[3].append(5)
graph[5].append(3)
graph[6].append(7)
graph[7].append(6)
longestConnectionPalin(V)
# This code is contributed by mohit kumar 29
C#
// C# implementation to check if
// longest connected component is
// palindrome in undirected graph
using System;
using System.Collections.Generic;
class GFG{
// Initializing bool array
// to mark visited vertices
static bool [] visited = new bool[10001];
// Container to store longest chain
static List<int>storeChain = new List<int>();
// Function to traverse
// the undirected graph
// using the Depth first
// traversal
static void depthFirst(int v,
List<int> []graph)
{
// Marking the visited
// vertex as true
visited[v] = true;
// Store the connected chain
storeChain.Add(v);
foreach (int i in graph[v])
{
if (visited[i] == false)
{
// Recursive call to
// the DFS algorithm
depthFirst(i, graph);
}
}
}
// Function to check that
// the connected component
// forms a palindrome
static void checkPalin(int []arr,
int n)
{
// Container to store the
// frequency of each occurring
// element
Dictionary<int,
int> frequency = new Dictionary<int,
int>();
// Container to visit elements
HashSet<int> element = new HashSet<int>();
for(int i = 0; i < n; i ++)
{
// If element has not been
// visited already the element
// is inserted with freq = 1
// frequency of occurrence,
// if visited already, then
// frequency is updated
if ((element.Contains(arr[i])))
{
frequency[arr[i]]++;
}
else
{
frequency.Add(arr[i], 1);
}
element.Add(arr[i]);
}
// Variable to store
// readonly result
int result = 1;
// For even array size, all
// the elements are checked
// for even occurrences, if
// odd array size, then it
// is checked if a single
// element with odd frequency
// is present or not
if (n % 2 == 0)
{
foreach(KeyValuePair<int, int> i in frequency)
{
if (i.Value % 2 != 0)
{
result = 0;
break;
}
}
}
else
{
int countFreq = 0;
foreach(KeyValuePair<int, int> i in frequency)
{
if (i.Value % 2 != 0)
{
countFreq ++;
}
}
if (countFreq != 1)
result = 0;
}
// Printing the
// readonly result
if (result == 0)
Console.Write("longest connected " +
"component is Palindrome");
else
Console.Write("longest connected " +
"component not a Palindrome");
}
// Function to check that longest
// connected component forms a palindrome
static void longestConnectionPalin(List<int> []graph,
int vertices,
List<int> values)
{
// maxChain stores the ;
// maximum chain size
int maxChain = 0;
// Container to store each chain
List<int> maxStoreChain = new List<int>();
// Following loop invokes
// DFS algorithm
for(int i = 1; i <= vertices; i++)
{
if (visited[i] == false)
{
// Variable to hold
// temporary length
int sizeChain;
// DFS algorithm
depthFirst(i, graph);
// Variable to hold each chain size
sizeChain = storeChain.Count;
if (sizeChain > maxChain)
{
maxChain = sizeChain;
maxStoreChain = storeChain;
}
}
}
// Container to store values
// of vertices of longest chain
int []longChainValues = new int[maxChain + 1];
// Storing the values of
// longest chain
for(int i = 0; i < maxChain; i ++)
{
int temp = values[maxStoreChain[i] - 1];
longChainValues[i] = temp;
}
// Function call to check
// for Palindrome
checkPalin(longChainValues,
maxChain);
}
// Driver code
public static void Main(String[] args)
{
// Initializing graph in the
// form of adjacency list
List<int> []graph = new List<int>[1001];
for(int i = 0; i < graph.Length; i++)
graph[i] = new List<int>();
// Defining the number of
// edges and vertices
//int E;
//E = 4;
int V;
V = 7;
// Assigning the values
// for each vertex of
// the undirected graph
List<int> values = new List<int>();
values.Add(10);
values.Add(25);
values.Add(5);
values.Add(15);
values.Add(5);
values.Add(20);
values.Add(0);
// Constructing the
// undirected graph
graph[1].Add(2);
graph[2].Add(1);
graph[3].Add(4);
graph[4].Add(3);
graph[3].Add(5);
graph[5].Add(3);
graph[6].Add(7);
graph[7].Add(6);
longestConnectionPalin(graph, V, values);
}
}
// This code is contributed by aashish1995
Javascript
<script>
// Javascript implementation to check if
// longest connected component is
// palindrome in undirected graph
// Initializing boolean array
// to mark visited vertices
let visited = new Array(10001);
// Container to store longest chain
let storeChain = [];
// Function to traverse
// the undirected graph
// using the Depth first
// traversal
function depthFirst(v, graph)
{
// Marking the visited
// vertex as true
visited[v] = true;
// Store the connected chain
storeChain.push(v);
for(let i = 0; i < graph[v].length; i++)
{
if (visited[graph[v][i]] == false)
{
// Recursive call to
// the DFS algorithm
depthFirst(graph[v][i], graph);
}
}
}
// Function to check that
// the connected component
// forms a palindrome
function checkPalin(arr, n)
{
// Container to store the
// frequency of each occurring
// element
let frequency = new Map();
// Container to visit elements
let element = new Set();
for(let i = 0; i < n; i ++)
{
// If element has not been
// visited already the element
// is inserted with freq = 1
// frequency of occurrence,
// if visited already, then
// frequency is updated
if ((element.has(arr[i])))
{
frequency.set(arr[i],
frequency.get(arr[i]) + 1);
}
else
{
frequency.set(arr[i], 1);
}
element.add(arr[i]);
}
// Variable to store
// final result
let result = 1;
// For even array size, all
// the elements are checked
// for even occurrences, if
// odd array size, then it
// is checked if a single
// element with odd frequency
// is present or not
if (n % 2 == 0)
{
for(let [key, value] of frequency.entries())
{
if (value % 2 != 0)
{
result = 0;
break;
}
}
}
else
{
let countFreq = 0;
for(let [key, value] of frequency.entries())
{
if(value % 2 != 0)
{
countFreq ++;
}
}
if (countFreq != 1)
result = 0;
}
// Printing the
// final result
if (result != 0)
document.write("Longest connected " +
"component is Palindrome");
else
document.write("Longest connected " +
"component not a Palindrome");
}
// Function to check that longest
// connected component forms a palindrome
function longestConnectionPalin(graph, vertices,
values)
{
// maxChain stores the ;
// maximum chain size
let maxChain = 0;
// Container to store each chain
let maxStoreChain = [];
// Following loop invokes
// DFS algorithm
for(let i = 1; i <= vertices; i++)
{
if (visited[i] == false)
{
// Variable to hold
// temporary length
let sizeChain;
// DFS algorithm
depthFirst(i, graph);
// Variable to hold each chain size
sizeChain = storeChain.size;
if (sizeChain > maxChain)
{
maxChain = sizeChain;
maxStoreChain = storeChain;
}
}
}
// Container to store values
// of vertices of longest chain
let longChainValues = new Array(maxChain + 1);
// Storing the values of
// longest chain
for(let i = 0; i < maxChain; i ++)
{
let temp = values.get(
maxStoreChain.get(i) - 1);
longChainValues[i] = temp;
}
// Function call to check
// for Palindrome
checkPalin(longChainValues,
maxChain);
}
// Driver code
let graph = new Array(1001);
for(let i = 0; i < graph.length; i++)
graph[i] = [];
// Defining the number of
// edges and vertices
let E, V;
E = 4;
V = 7;
// Assigning the values
// for each vertex of
// the undirected graph
let values = [];
values.push(10);
values.push(25);
values.push(5);
values.push(15);
values.push(5);
values.push(20);
values.push(0);
// Constructing the
// undirected graph
graph[1].push(2);
graph[2].push(1);
graph[3].push(4);
graph[4].push(3);
graph[3].push(5);
graph[5].push(3);
graph[6].push(7);
graph[7].push(6);
longestConnectionPalin(graph, V, values);
// This code is contributed by unknown2108
</script>
Longest connected component is Palindrome
Tiempo Complejidad: O(V + E)
Espacio Auxiliar: O(V + E)
Publicación traducida automáticamente
Artículo escrito por PratikBasu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA