1. Montón:
un montón es una estructura de datos basada en un árbol en el que el árbol debería estar casi completo. Es de dos tipos, es decir, montón máximo y mínimo.
- Montón máximo: en el montón máximo, si p es el padre y c es su hijo, entonces para cada padre p el valor de él es mayor o igual que el valor de c
- Montón mínimo En el montón mínimo, si p es el padre y c es su hijo, entonces para cada padre el valor de p es menor o igual que el valor de c.
Heap también se usa como cola de prioridad. En qué elemento más alto (en el caso del montón máximo) o más bajo (en el caso del montón mínimo) está presente en la raíz.
Heap se usa en problemas en los que necesitamos eliminar el elemento de mayor o menor prioridad. Una implementación común del montón es el montón binario.
Implementación
- Aunque el montón se puede implementar como un árbol, se desperdiciará mucho almacenamiento para almacenar punteros. Debido a la propiedad del montón de ser un árbol binario completo, se puede almacenar fácilmente en una array.
- Donde el elemento raíz se almacena en el primer índice y su índice secundario se puede calcular de la siguiente manera.
- Índice hijo izquierdo = 2×r donde r es el índice de la raíz y el índice inicial de la array es 1.
- Índice del niño derecho = 2×r+1.
- Y el índice principal se puede calcular como piso (i/2) donde i es el índice de su hijo izquierdo o derecho.
Ejemplo:
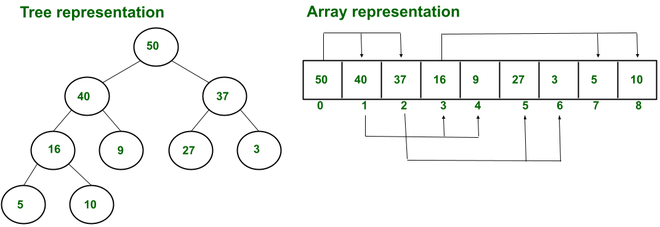
Ejemplo de montón máximo
2. Array ordenada:
una array ordenada es una estructura de datos en la que los elementos se clasifican en orden numérico, alfabético o por algún otro orden y se almacenan en ubicaciones de memoria contiguas .

Ejemplo de array ordenada
- Todas las estructuras de datos tienen sus pros y sus contras dependiendo de los problemas o algoritmos donde se utilicen. Por ejemplo , el montón es la mejor estructura de datos en situaciones en las que necesitamos la optimización para encontrar (máximo o mínimo con frecuencia), eliminar (máximo o mínimo) o insertar (máximo o mínimo) elemento.
- Y la array ordenada se usa en situaciones en las que los elementos deben almacenarse en orden ascendente o descendente. Por ejemplo: en los algoritmos de programación de trabajo más corto primero donde los procesos (almacenados en una array) deben ordenarse de acuerdo con el tiempo de ráfaga de los procesos. Entonces, en caso de que se requiera una array de clasificación.
| Estructura de datos | Insertar | Búsqueda | encontrar min | Eliminar mínimo |
|---|---|---|---|---|
| array ordenada | En) | O (registro n) | O(1) | En) |
| montón mínimo | O (registro n) | En) | O(1) | O (registro n) |
Diferencia entre montones y array ordenada:
|
array ordenada |
Muchísimo |
|---|---|
| En una array ordenada, los elementos se clasifican en orden numérico, alfabético o por algún otro orden y se almacenan en ubicaciones de memoria contiguas. | Un montón es un árbol binario casi completo. En el caso del montón máximo, si p es el padre y c es su hijo, entonces el valor de p es mayor o igual que el valor de c y en el montón mínimo si p es el padre y c es su hijo, entonces el valor de p es menor o igual que el valor de c. |
| Una array ordenada puede actuar como un montón cuando se usa una implementación de montón basada en una array. | El montón puede o no ser una array ordenada cuando se usa la implementación de montón basada en array. |
| Para un conjunto dado de enteros, puede haber dos arreglos (es decir, ascendente o descendente) posibles después de la clasificación. |
Para un conjunto dado de n enteros, se pueden formar múltiples montones posibles (máximo o mínimo). Consulte este artículo para obtener más detalles. |
| Aquí se puede acceder a la siguiente dirección del elemento incrementando el índice del elemento actual. | Aquí se puede acceder al índice secundario izquierdo calculando 2 × r y se puede acceder al índice del elemento derecho calculando 2 × r + 1, donde r es el índice de la raíz y la array se basa en 1 índice. |
| La búsqueda se puede realizar en tiempo O (log n) en una array ordenada mediante la búsqueda binaria. | El almacenamiento dinámico no es óptimo para la operación de búsqueda, pero la búsqueda se puede realizar con una complejidad O(n). |
| La ordenación de montón se puede usar para ordenar una array, pero para este primer montón se construye con una array de n enteros y luego se aplica la ordenación de montón. Aquí se necesita una complejidad de tiempo O (n) para construir el montón y se requiere O (n log n) para eliminar n (mínimo o máximo) elemento del montón y colocarlo al final de la array y disminuir el tamaño de la array). | Clasificación de montón que se aplica en montones (mínimo o máximo) y es un algoritmo de clasificación en el lugar para realizar la clasificación en complejidad de tiempo O (n log n). |
| Ordenar una array requiere una complejidad O (n log n), que es la mejor complejidad de tiempo para ordenar una array de n elementos en un algoritmo de clasificación basado en comparación. | La construcción del montón requiere una complejidad de tiempo O(n). |
| Las arrays ordenadas se utilizan para realizar búsquedas eficientes (es decir, búsquedas binarias), algoritmos de programación SJFS y en las organizaciones donde se necesitan datos en orden ordenado, etc. | Los montones se utilizan en la clasificación de montones, la cola de prioridad, los algoritmos gráficos y la combinación de vías K, etc. |
Publicación traducida automáticamente
Artículo escrito por goutamnagpal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA