Modificar una array reemplazando cada elemento con el máximo de su suma diagonal izquierda o derecha

Dada una array mat[][] con dimensiones M * N , la tarea es reemplazar cada elemento de la array con la suma máxima de su diagonal izquierda o derecha.

Ejemplos:

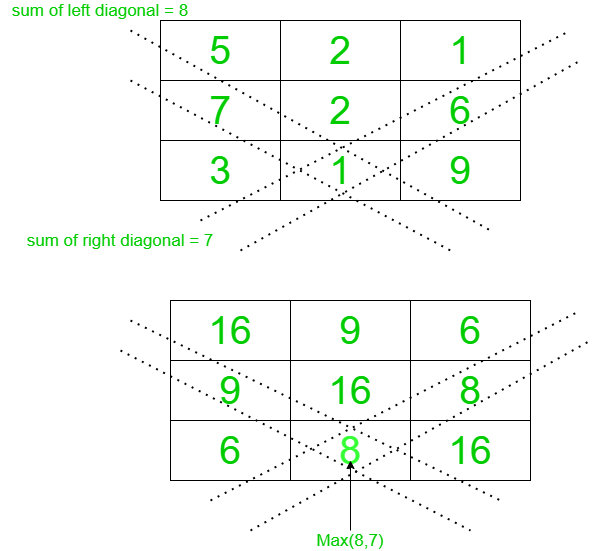
Entrada: mat[][] = {{5, 2, 1}, {7, 2, 6}, {3, 1, 9}}
Salida: 
16 9 6 
9 16 8
6 8 16
Explicación:
Reemplace cada elemento con max(suma de la diagonal derecha, suma de la diagonal izquierda).
Siga el diagrama a continuación para entender más claramente.

Entrada: mat[][] = {{1, 2}, {3, 4}}
Salida: 
5 5
5 5

Enfoque: La idea principal se basa en los hechos basados ​​en la observación que se indica a continuación:

• La suma de los índices de fila y columna para los elementos de la diagonal derecha es igual.
• La diferencia entre los índices de fila y columna para los elementos de la diagonal izquierda es igual.
• Usando las dos propiedades anteriores para almacenar la suma de las diagonales izquierda y derecha de cada elemento usando un Map .
• Recorra la array y reemplace cada elemento con el máximo de la suma de la diagonal izquierda o la suma de la diagonal derecha.
• Imprimir la array final obtenida.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to update given matrix with
// maximum of left and right diagonal sum
void updateMatrix(int mat[][3])
{
 
  // Stores the total sum
  // of right diagonal
  map<int, int> right;
 
  // Stores the total sum
  // of left diagonal
  map<int, int> left;
 
  for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 3; j++) {
 
      // Update the map storing
      // right diagonal sums
      if (right.find(i + j) == right.end())
        right[i + j] = mat[i][j];
      else
        right[i + j] += mat[i][j];
 
      // Update the map storing
      // left diagonal sums
      if (left.find(i - j) == left.end())
        left[i - j] = mat[i][j];
      else
        left[i - j] += mat[i][j];
    }
  }
   
  // Traverse the matrix
  for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 3; j++) {
 
      // Update the matrix
      mat[i][j] = max(right[i + j], left[i - j]);
    }
  }
 
  // Print the matrix
  for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 3; j++) {
      cout << mat[i][j] << " ";
    }
    cout << endl;
  }
}
 
// Driver code
int main()
{
  int mat[][3]
    = { { 5, 2, 1 }, { 7, 2, 6 }, { 3, 1, 9 } };
  updateMatrix(mat);
  return 0;
}
 
// This code is contributed by ukasp.

// Java program for the above approach
  
// Function to update given matrix with
// maximum of left and right diagonal sum
import java.io.*;
import java.util.*;
 
class GFG {
     
    static void updateMatrix(int mat[][])
    {
        Map<Integer, Integer> right
            = new HashMap<Integer, Integer>(); 
             
        Map<Integer, Integer> left
            = new HashMap<Integer, Integer>();     
             
        for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
        {
              
            // Update the map storing
            // right diagonal sums
            if (!right.containsKey(i + j))
                right.put(i + j, mat[i][j]);
            else
                right.put(i + j,
                right.get(i + j) + mat[i][j]);
  
            // Update the map storing
            // left diagonal sums
            if (!left.containsKey(i - j))
                left.put(i - j, mat[i][j]);
  
            else
                left.put(i - j,
                left.get(i - j) + mat[i][j]);
        }
    }
  
    // Traverse the matrix
    for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
        {
              
            // Update the matrix
            mat[i][j] = Math.max(right.get(i + j),
                                  left.get(i - j));
        }
    }
  
    // Print the matrix
    for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
        {
            System.out.print(mat[i][j] + " ");
        }
        System.out.print("\n");
    }   
    }
     
    // Driver code
    public static void main (String[] args) {
        int[][] mat = {{ 5, 2, 1 },
            { 7, 2, 6 },
            { 3, 1, 9 }};
            updateMatrix(mat);
    }
}
 
// This code is contributed by avanitrachhadiya2155

# Python3 program for the above approach
 
# Function to update given matrix with
# maximum of left and right diagonal sum
def updateMatrix(mat):
 
    # Stores the total sum
    # of right diagonal
    right = {}
 
    # Stores the total sum
    # of left diagonal
    left = {}
 
    for i in range(len(mat)):
        for j in range(len(mat[0])):
 
            # Update the map storing
            # right diagonal sums
            if i + j not in right:
                right[i + j] = mat[i][j]
            else:
                right[i + j] += mat[i][j]
 
            # Update the map storing
            # left diagonal sums
            if i-j not in left:
                left[i-j] = mat[i][j]
            else:
                left[i-j] += mat[i][j]
 
    # Traverse the matrix
    for i in range(len(mat)):
        for j in range(len(mat[0])):
 
            # Update the matrix
            mat[i][j] = max(right[i + j], left[i-j])
 
    # Print the matrix
    for i in mat:
        print(*i)
 
# Given matrix
mat = [[5, 2, 1], [7, 2, 6], [3, 1, 9]]
updateMatrix(mat)

// C# program for the above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG
{
    // Function to update given matrix with
    // maximum of left and right diagonal sum
    static void updateMatrix(int[,] mat)
    {
      
      // Stores the total sum
      // of right diagonal
      Dictionary<int, int> right = new Dictionary<int, int>();
      
      // Stores the total sum
      // of left diagonal
      Dictionary<int, int> left = new Dictionary<int, int>();
      
      for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
      
          // Update the map storing
          // right diagonal sums
          if (!right.ContainsKey(i + j))
            right[i + j] = mat[i,j];
          else
            right[i + j] += mat[i,j];
      
          // Update the map storing
          // left diagonal sums
          if (!left.ContainsKey(i - j))
            left[i - j] = mat[i,j];
          else
            left[i - j] += mat[i,j];
        }
      }
        
      // Traverse the matrix
      for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
      
          // Update the matrix
          mat[i,j] = Math.Max(right[i + j], left[i - j]);
        }
      }
      
      // Print the matrix
      for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
          Console.Write(mat[i,j] + " ");
        }
        Console.WriteLine();
      }
    }
     
  static void Main ()
  {
    int[,] mat = { { 5, 2, 1 }, { 7, 2, 6 }, { 3, 1, 9 } };
    updateMatrix(mat);
  }
}
 
// This code is contributed by suresh07.

<script>
 
// Javascript program for the above approach
 
// Function to update given matrix with
// maximum of left and right diagonal sum
function updateMatrix(mat)
{
     
    // Stores the total sum
    // of right diagonal
    let right = new Map();
 
    // Stores the total sum
    // of left diagonal
    let left = new Map();
 
    for(let i = 0; i < 3; i++)
    {
        for(let j = 0; j < 3; j++)
        {
             
            // Update the map storing
            // right diagonal sums
            if (!right.has(i + j))
                right.set(i + j, mat[i][j]);
            else
                right.set(i + j,
                right.get(i + j) + mat[i][j]);
 
            // Update the map storing
            // left diagonal sums
            if (!left.has(i - j))
                left.set(i - j, mat[i][j]);
 
            else
                left.set(i - j,
                left.get(i - j) + mat[i][j]);
        }
    }
 
    // Traverse the matrix
    for(let i = 0; i < 3; i++)
    {
        for(let j = 0; j < 3; j++)
        {
             
            // Update the matrix
            mat[i][j] = Math.max(right.get(i + j),
                                  left.get(i - j));
        }
    }
 
    // Print the matrix
    for(let i = 0; i < 3; i++)
    {
        for(let j = 0; j < 3; j++)
        {
            document.write(mat[i][j] + " ");
        }
        document.write("<br>");
    }
}
 
// Driver code
let mat = [ [ 5, 2, 1 ],
            [ 7, 2, 6 ],
            [ 3, 1, 9 ] ];
updateMatrix(mat);
 
// This code is contributed by gfgking.
 
</script>

16 9 6
9 16 8
6 8 16

Complejidad de Tiempo: O(N * M)
Espacio Auxiliar: O(N * M)