Tipos de transformación:
- Transformación de traducción
- Transformación de escala
- Transformación de rotación
- Transformación de corte
- Transformación de reflexión
Nota: si se nos pide que realicemos tres o más tipos diferentes de transformaciones sobre un punto (P 0 ) simultáneamente que se coloca en el espacio 3D, y supongamos que estas transformaciones son T 1 , T 2 y T 3 respectivamente, entonces en este caso que haremos?
Entonces, veremos las siguientes soluciones.
a) Obviamente, primero aplicando series de Transformaciones una por una sobre las coordenadas del objeto secuencialmente.
Primero realizamos la transformación T 1, luego P o se transforma en P 1.
En segundo lugar, realizamos la transformación T 2y el punto P 1 se transforma en P 2.
Por último, realizamos la transformación T 3 y obtenemos el resultado final, es decir; P 3, y obtendremos nuestra última coordenada del punto transformado (P 3 ).
b) Segunda solución, aplicando transformación Compuesta en un solo disparo.
![Rendered by QuickLaTeX.com \mathbf{P_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_0[x_0\hspace{0.2cm}y_0\hspace{0.2cm}z_0\hspace{0.2cm}1].T_1} \newline \hspace{5.87cm}\mathbf{P_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_1\hspace{0.2cm}y_1\hspace{0.2cm}z_1]} \\ \hspace{4.37cm}\mathbf{P_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_1[x_1\hspace{0.2cm}y_1\hspace{0.2cm}z_1\hspace{0.2cm}1].T_2} \newline \hspace{5.87cm}\mathbf{P_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_2\hspace{0.2cm}y_2\hspace{0.2cm}z_2]} \newline \hspace{4.37cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_2[x_2\hspace{0.2cm}y_2\hspace{0.2cm}z_2\hspace{0.2cm}1].T_3} \newline \hspace{5.87cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_3\hspace{0.2cm}y_3\hspace{0.2cm}z_3]}\\ \textbf {But the idea that is concerned in Composite Transformation is} \newline \textbf{slightly different, that we'll discuss in detail in the following article.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2b879dda5a3b1fc3e31cad2c8a1ddc3_l3.png)
Nota: Aquí T 1 , T 2 , T 3 corresponden a su condición de array de transformación.
Como su propio nombre sugiere compuesto, aquí componemos dos o más de dos transformaciones juntas y calculamos una array de transformación resultante (R) multiplicando todas las condiciones de array de transformación correspondientes entre sí.
El mismo resultado equivalente que obtuvimos sobre el punto P 0 y lo transformamos en P 3 en el ejemplo anterior también se puede lograr multiplicando directamente la resultante R con el punto P 0 en lugar de realizar las transformaciones T 1 , T 2 y T 3 secuencialmente uno luego de una.
![Rendered by QuickLaTeX.com \mathbf{R=[T_1*T_2*T_3]} \newline \hspace{4.37cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=P_0[x_0\hspace{0.2cm}y_0\hspace{0.2cm}z_0\hspace{0.2cm}1].R} \\ \hspace{5.87cm}\mathbf{P_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[x_3\hspace{0.2cm}y_3\hspace{0.2cm}z_3]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-467fc950ba14904f1611ef6546104f8f_l3.png)
Y terminamos con el mismo resultado equivalente que obtuvimos en nuestro ejemplo anterior.
Problema: Considere que tenemos un paralelepípedo «OABCDEFG» sobre el que queremos realizar
- Transformación de traslación (T 1 ) si las distancias de traslación son D x =2, D y =3, D z =2 ,entonces
- Transformación de escala (T 2 ) si los factores de escala son s x = 2, s y = 1, s z = 3 y, por último, realiza,
- Transformación de corte (T 3 ) en la dirección x si los factores de corte son s y =2 y s z =1.
Solución: Nos dan el siguiente paralelepípedo
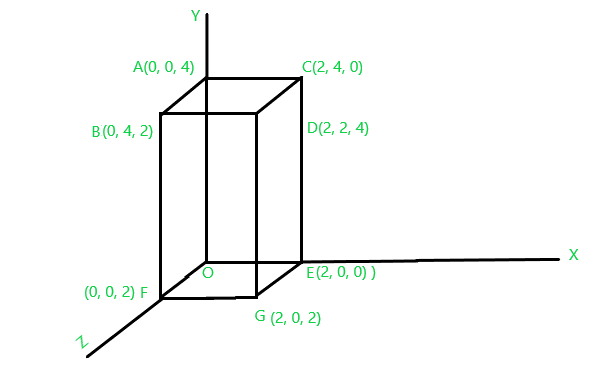
Figura 1
Primero, realizamos la transformación de traducción T1:
La array de transformación de traducción se muestra como:
![Rendered by QuickLaTeX.com \mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f36cdff35de11139b78596d588a090be_l3.png) [Tex]\hspace{4.37cm}\mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.} [/Tex]
[Tex]\hspace{4.37cm}\mathbf{T_1=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}D_x=2,D_y=3\hspace{0.2cm} and\hspace{0.2cm} D_z=3\hspace{0.2cm} are\hspace{0.2cm}translation\hspace{0.2cm} distances.} [/Tex]
Ahora aplique esta condición de array de transformación de traslación sobre las coordenadas:
Para la coordenada O[0 0 0], la nueva coordenada traducida sería O 1 :
![Rendered by QuickLaTeX.com \mathbf{O_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{O_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-922d14dc895eb80c7276b3f11b449727_l3.png)
Para la coordenada A[0 0 4], la nueva coordenada traducida sería A 1 :
![Rendered by QuickLaTeX.com \mathbf{A_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{A_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d38994ba76df0036934610476e68c92_l3.png)
Para la coordenada B[0 4 2], la nueva coordenada traducida sería B 1 :
![Rendered by QuickLaTeX.com \mathbf{B_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B[0\hspace{0.2cm}4\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[2\hspace{0.2cm}7\hspace{0.2cm}4\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{B_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}7\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3665cee50645079c5e9d11a25ed4dbb_l3.png)
Para la coordenada C[2 4 0], la coordenada recién traducida sería C 1 :
![Rendered by QuickLaTeX.com \mathbf{C_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C[2\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}7\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{C_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}7\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f97c7aad24df8372eae818c7efd67fa_l3.png)
Para la coordenada D[2 2 4], la nueva coordenada traducida sería D 1 :
![Rendered by QuickLaTeX.com \mathbf{D_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D[2\hspace{0.2cm}2\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}5\hspace{0.2cm}6\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{D_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}5\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac05ca0b3f7c4ba13c776ca6e556a4e8_l3.png)
Para la coordenada E[2 0 0], la nueva coordenada traducida sería E 1 :
![Rendered by QuickLaTeX.com \mathbf{E_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E[2\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8302a6077300b7873c3e009f700c39c4_l3.png)
Para la coordenada F[0 0 2], la nueva coordenada traducida sería F 1 :
![Rendered by QuickLaTeX.com \mathbf{F_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F[0\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[2\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[2\hspace{0.2cm}3\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46b88e7ac963f080d523ed8f2fbe1401_l3.png)
Para la coordenada G[2 0 2], la nueva coordenada traducida sería G 1 :
![Rendered by QuickLaTeX.com \mathbf{G_1[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G[2\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_1[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-476afc6badfe3225bb9079f5f0a796e2_l3.png)

Figura 2
En segundo lugar, se dice que realizamos la transformación de escala T 2 :
La array de transformación de escala se muestra como:
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{T_2=\left[\begin{matrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\D_x&D_y&D_z&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}s_x=2,s_y=1\hspace{0.2cm} and\hspace{0.2cm} s_z=3\hspace{0.2cm} are\hspace{0.2cm}Scaling\hspace{0.2cm}parameter.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6dc4aacdd490889ad648695e336127e8_l3.png)
Ahora aplique esta condición de array de transformación de escala sobre las coordenadas:
Para la coordenada O 1 [2 3 2], la nueva coordenada escalada sería O 2 :
![Rendered by QuickLaTeX.com \mathbf{O_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O_1[2\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{O_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85a0c0f9309dc2964f0d72e6f4aaaa41_l3.png)
Para la coordenada A 1 [2 3 6], la nueva coordenada escalada sería A 2 :
![Rendered by QuickLaTeX.com \mathbf{A_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A_1[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}18\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}18]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c3229f9e6feab34f5ed00903960d57f_l3.png)
Para la coordenada B 1 [2 7 4], la nueva coordenada escalada sería B 2 :
![Rendered by QuickLaTeX.com \mathbf{B_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B_1[2\hspace{0.2cm}7\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}7\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{B_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}7\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb874ffc5afcec6f79a29850502f2cfd_l3.png)
Para la coordenada C 1 [4 7 2], la nueva coordenada escalada sería C 2 :
![Rendered by QuickLaTeX.com \mathbf{C_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C_1[2\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}7\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}7\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-635affa20cf5eec1bd27162583bf04ef_l3.png)
Para la coordenada D 1 [4 5 6], la nueva coordenada escalada sería D 2 :
![Rendered by QuickLaTeX.com \mathbf{D_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D_1[4\hspace{0.2cm}5\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}5\hspace{0.2cm}18\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{D_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}5\hspace{0.2cm}18]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08a5f637b881022732b493fc699a39a2_l3.png)
Para la coordenada E 1 [4 3 2], la nueva coordenada escalada sería E 2 :
![Rendered by QuickLaTeX.com \mathbf{E_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E_1[4\hspace{0.2cm}3\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}3\hspace{0.2cm}6]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b8a3f40cc62dfe111538530cdd2fc2a_l3.png)
Para la coordenada F 1 [2 3 4], la nueva coordenada escalada sería F 2 :
![Rendered by QuickLaTeX.com \mathbf{F_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F_1[2\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}3\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d94164639c65153d5a3625668d69cc74_l3.png)
Para la coordenada G 1 [4 3 4], la nueva coordenada escalada sería G 2 :
![Rendered by QuickLaTeX.com \mathbf{G_2[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G_1[4\hspace{0.2cm}3\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_2[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}3\hspace{0.2cm}12]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73d1c28bbb7590c989491f11a1e2b5b5_l3.png)

Fig. 3
Por último, realizamos la transformación de corte T 3 en la dirección x:
La array de transformación de corte para la dirección x se muestra como:
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{T_3=\left[\begin{matrix}1&sh_y&sh_z&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \mathbf{Where \hspace{0.2cm}sh_y=2\hspace{0.2cm}and\hspace{0.2cm}sh_z=1\hspace{0.2cm}are\hspace{0.2cm}Shearing\hspace{0.2cm}parameter.}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f75e4183fead684ccb775327b3726cbb_l3.png)
Ahora, aplique esta condición de array de transformación de corte sobre las coordenadas:
Para la coordenada O 2 [4 3 6], la nueva coordenada escalada sería O 3 :
![Rendered by QuickLaTeX.com \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O_2[4\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}10\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}10]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ef986647129a88f4e65053ff7071285_l3.png)
Para la coordenada A 2 [4 3 18], la nueva coordenada escalada sería A 3 :
![Rendered by QuickLaTeX.com \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A_2[4\hspace{0.2cm}3\hspace{0.2cm}18\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}22\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}22]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-16b567b04c2ca915d130de89e9e2d9cf_l3.png)
Para la coordenada B 2 [4 7 12], la nueva coordenada escalada sería B 3 :
![Rendered by QuickLaTeX.com \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B_2[4\hspace{0.2cm}7\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}15\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}15\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8f803827e089d9fb55be5318decf964f_l3.png)
Para la coordenada C 2 [8 7 6], la nueva coordenada escalada sería C 3 :
![Rendered by QuickLaTeX.com \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C_2[8\hspace{0.2cm}7\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}23\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}23\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b1ce752ecc98d24f210fdfa6e4ee65b_l3.png)
Para la coordenada D 2 [8 5 18], la nueva coordenada escalada sería D 3 :
![Rendered by QuickLaTeX.com \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D_2[8\hspace{0.2cm}6\hspace{0.2cm}18\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}21\hspace{0.2cm}26\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}21\hspace{0.2cm}26]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3004d4ea91076d13ca8709641f557dee_l3.png)
Para la coordenada E 2 [8 7 6], la nueva coordenada escalada sería E 3 :
![Rendered by QuickLaTeX.com \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E_2[8\hspace{0.2cm}3\hspace{0.2cm}6\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c804ea8a97cadb392b4941e755347eb_l3.png)
Para la coordenada F 2 [4 3 12], la nueva coordenada escalada sería F 3 :
![Rendered by QuickLaTeX.com \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F_2[4\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cab7ab12d1374db182ee681743486e5_l3.png)
Para la coordenada G 2 [8 3 12], la nueva coordenada escalada sería G 3 :
![Rendered by QuickLaTeX.com \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G_2[8\hspace{0.2cm}3\hspace{0.2cm}12\hspace{0.2cm}1]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}20\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}20]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e05e987410f86171a2ae0b74642f1471_l3.png)
Finalmente, obtenemos nuestro objeto inclinado redimensionado en la dirección x después de realizar las transformaciones T 1 , T 2 y T 3 .

Figura 4
Solución a través de Transformación Compuesta
El resultado final, que obtuvimos arriba para el cuboide «OABCDEF» al aplicar la transformación T 1 , T 2 y T 3 una tras otra en orden secuencial, también se podría obtener el mismo resultado equivalente utilizando el concepto de Transformación compuesta. Para realizar la transformación compuesta, primero debemos calcular la array de transformación resultante (R) combinando todas las representaciones de array de transformación distinguidas.
La array de transformación resultante se calcularía de la siguiente manera:
La transformación resultante se calculará multiplicando la array de transformación de traducción con la array de transformación de escala y la multiplicación resultante (R 2 ) de ambas se multiplicará por la última array de transformación de corte dada.
![Rendered by QuickLaTeX.com \hspace{4.37cm}\mathbf{R_2=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&3&2&1\end{matrix}\right]*\mathbf{\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&1\end{matrix}\right]}} \\ \newline\hspace{4.37cm}\mathbf{R_2=\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\4&3&6&1\end{matrix}\right]}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e5a3f27c0c28a686650cfa2d84080d2_l3.png)
Ahora, multiplique R2 con la array de transformación de corte para obtener la resultante R:
![Rendered by QuickLaTeX.com \mathbf{R=R_2*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\\hspace{2.87cm}\mathbf{R=\left[\begin{matrix}2&0&0&0\\0&1&0&0\\0&0&3&0\\4&3&6&1\end{matrix}\right]*\left[\begin{matrix}1&2&1&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]}\\ \newline \hspace{4.15cm} \mathbf{R=\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-94e723cf5a255f836ce4c6e7fb87ad03_l3.png) \
\
Ahora, aplique esta condición de array de transformación resultante sobre las coordenadas:
Para la coordenada O[0 0 0], la nueva coordenada escalada sería O 3 :
![Rendered by QuickLaTeX.com \mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=O[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}10\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{O_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}10]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3f49451a249589ee6c6a9d8542b7ca2_l3.png)
Para la coordenada A[0 0 4], la nueva coordenada escalada sería A 3 :
![Rendered by QuickLaTeX.com \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=A[0\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}22\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{A_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}22]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a95d2bfb9008e3add501afa221e89bf_l3.png)
Para la coordenada B[0 4 2], la nueva coordenada escalada sería B 3 :
![Rendered by QuickLaTeX.com \mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=B[0\hspace{0.2cm}4\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}15\hspace{0.2cm}16\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{B_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}15\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b89daa3ed2c21a50dae97c58ecfb35bd_l3.png)
Para la coordenada C[2 4 0], la nueva coordenada escalada sería C 3 :
![Rendered by QuickLaTeX.com \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=C[2\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}23\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{C_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}23\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41e3f18379dd82fc64f8434a5416143d_l3.png)
Para la coordenada D[2 2 4], la nueva coordenada escalada sería D 3 :
![Rendered by QuickLaTeX.com \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=D[2\hspace{0.2cm}2\hspace{0.2cm}4\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}21\hspace{0.2cm}26\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{D_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}21\hspace{0.2cm}26]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0cb6c42abe868bab5fb7ae750df76bd5_l3.png)
Para la coordenada E[2 0 0], la nueva coordenada escalada sería E 3 :
![Rendered by QuickLaTeX.com \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=E[2\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\\hspace{6.52cm} \mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}14\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{E_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}14]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0679801d13d09bc3f25479ed63e7652d_l3.png)
Para la coordenada F[0 0 2], la nueva coordenada escalada sería F 3 :
![Rendered by QuickLaTeX.com \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=F[0\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[4\hspace{0.2cm}11\hspace{0.2cm}16\hspace{0.2cm}1]} \\\hspace{4.15cm} \mathbf{F_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[4\hspace{0.2cm}11\hspace{0.2cm}16]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2085357673f277b0ea22f3f072d9ba8_l3.png)
Para la coordenada G[2 0 2], la nueva coordenada escalada sería G 3 :
![Rendered by QuickLaTeX.com \mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=G[2\hspace{0.2cm}0\hspace{0.2cm}2\hspace{0.2cm}1]*\left[\begin{matrix}2&4&2&0\\0&1&0&0\\0&0&3&0\\4&11&10&1\end{matrix}\right]}\\ \\ \hspace{6.52cm}\mathbf{=[8\hspace{0.2cm}19\hspace{0.2cm}20\hspace{0.2cm}1]} \\ \hspace{4.15cm}\mathbf{G_3[x\hspace{0.2cm}y\hspace{0.2cm}z]=[8\hspace{0.2cm}19\hspace{0.2cm}20]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5cde8e87216fb9789a4a720b9ac2a562_l3.png)
Aquí, obtenemos nuestro resultado final en una sola toma:

Figura 5
Publicación traducida automáticamente
Artículo escrito por madhav_mohan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA