Consulte primero los conjuntos anteriores del artículo Proto Van Emde Boas Tree . Es muy recomendable.
Procedimiento para encontrar el mínimo:
- Caso base: si el tamaño de Proto-VEB es 2, devolveremos la clave más pequeña presente en el grupo; si no hay claves presentes, devolveremos -1 como el símbolo de que no hay claves presentes.
- Recursividad:
- Comenzaremos la recursión sobre el resumen hasta que alcancemos el primer valor verdadero (en el código, primero no nullptr en el grupo de resumen) que muestra que hay una clave presente en ese grupo.
- Ahora encontraremos la posición de la clave en ese grupo usando nuevamente una llamada recursiva sobre un grupo para encontrar el primer valor verdadero (en el código, primero no nullptr en el grupo) en un grupo como lo hemos hecho anteriormente.
- Finalmente, devolveremos el índice de esa clave según el número de grupo que obtengamos del procedimiento sobre el resumen y la posición que obtengamos del procedimiento sobre el grupo en el último paso.
Vea la imagen a continuación para obtener una comprensión básica de la operación:
Observe los círculos de color verde claro de arriba a abajo:
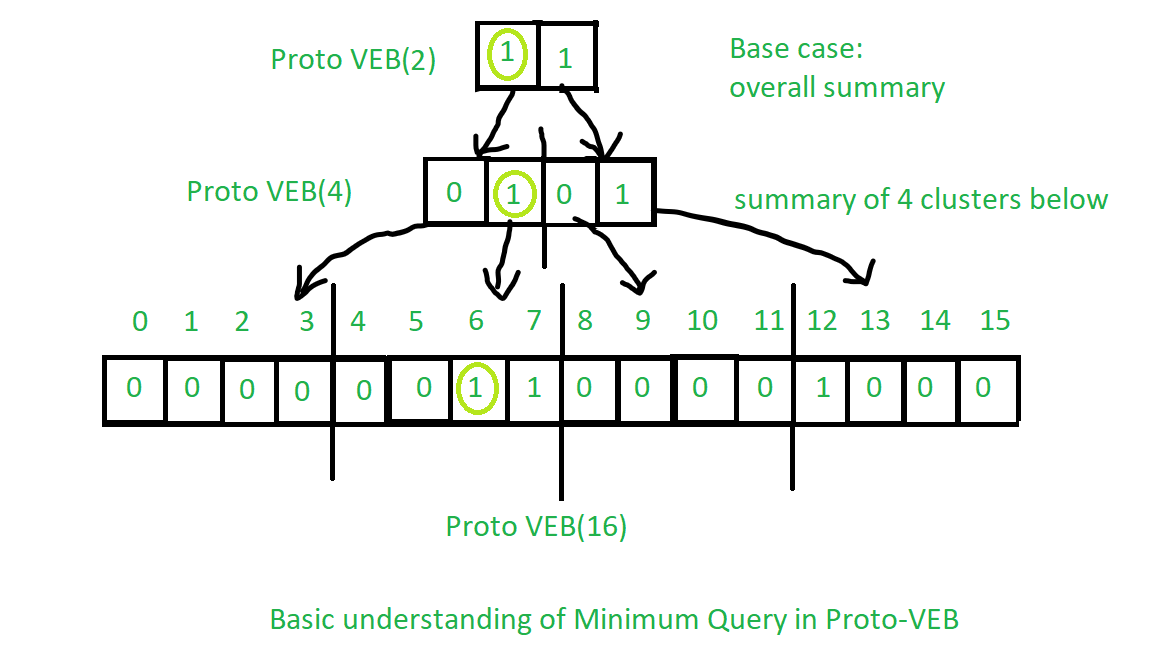
Vea la imagen a continuación para ver el funcionamiento mínimo real de Proto – VEB:
Siga las instrucciones en orden de numeración.
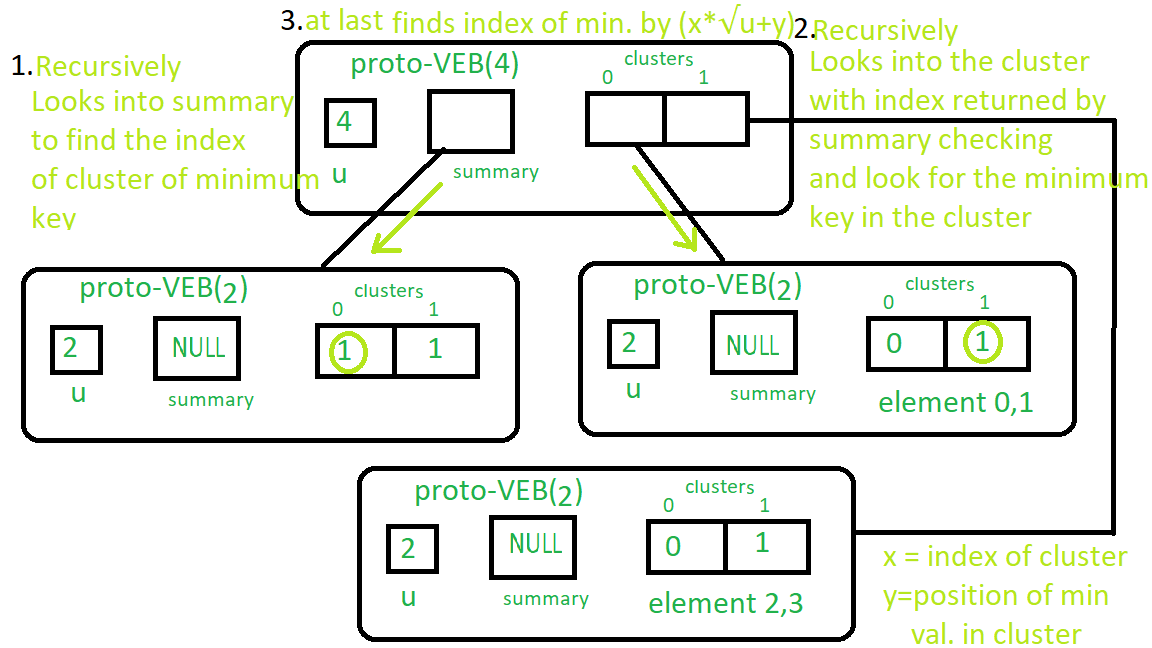
Puede obtener fácilmente la idea de Máximo a partir del procedimiento mínimo. Vea la imagen a continuación:
Observe los círculos de color verde claro de arriba a abajo:
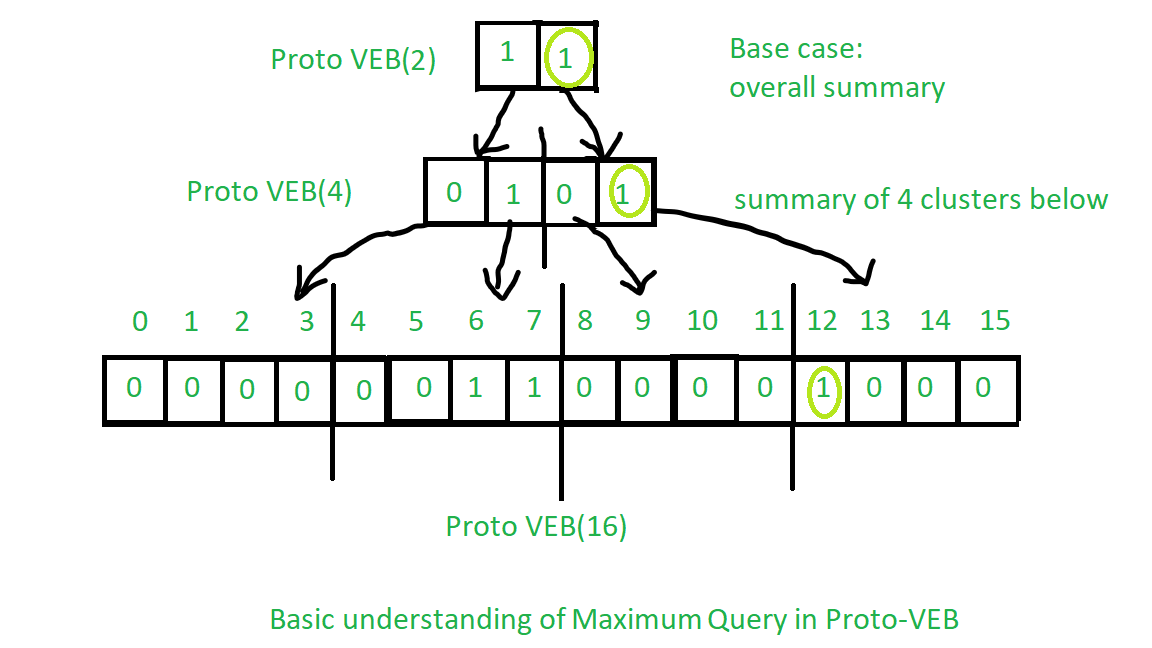
Implementación del algoritmo anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
class Proto_Van_Emde_Boas {
public:
// Total number of keys
int universe_size;
// Summary
Proto_Van_Emde_Boas* summary;
// Clusters array of Proto-VEB pointers
vector<Proto_Van_Emde_Boas*> clusters;
int root(int u)
{
return (int)sqrt(u);
}
// Function to return cluster numbers
// in which key is present
int high(int x)
{
return x / root(universe_size);
}
// Function to return position of x in cluster
int low(int x)
{
return x % root(universe_size);
}
// Function to return the index from
// cluster number and position
int generate_index(int cluster, int position)
{
return cluster * root(universe_size) + position;
}
// Constructor
Proto_Van_Emde_Boas(int size)
{
universe_size = size;
// Base case
if (size <= 2) {
// Set summary to nullptr as there is no
// more summary for size 2
summary = nullptr;
// Vector of two pointers
// nullptr in starting
clusters = vector<Proto_Van_Emde_Boas*>(size, nullptr);
}
else {
// Assigning Proto-VEB(sqrt(u)) to summary
summary = new Proto_Van_Emde_Boas(root(size));
// Creating array of Proto-VEB Tree pointers of size sqrt(u)
// first all nullptrs are going to assign
clusters = vector<Proto_Van_Emde_Boas*>(root(size), nullptr);
// Assigning Proto-VEB(sqrt(u)) to all its clusters
for (int i = 0; i < root(size); i++) {
clusters[i] = new Proto_Van_Emde_Boas(root(size));
}
}
}
};
// Function that returns true if the
// key is present in the tree
bool isMember(Proto_Van_Emde_Boas* helper, int key)
{
// If key is greater then universe_size then
// returns false
if (key >= helper->universe_size)
return false;
// If we reach at base case
// the just return whether
// pointer is nullptr then false
// else return true
if (helper->universe_size == 2) {
return helper->clusters[key];
}
else {
// Recursively go deep into the
// level of Proto-VEB tree using its
// cluster index and its position
return isMember(helper->clusters[helper->high(key)],
helper->low(key));
}
}
// Function to insert a key in the tree
void insert(Proto_Van_Emde_Boas*& helper, int key)
{
// If we reach at base case
// then assign Proto-VEB(1) in place
// of nullptr
if (helper->universe_size == 2) {
helper->clusters[key] = new Proto_Van_Emde_Boas(1);
}
else {
// Recursively using index of cluster and its
// position in cluster
insert(helper->clusters[helper->high(key)],
helper->low(key));
// Also do the same recursion in summary VEB
insert(helper->summary, helper->high(key));
}
}
// Function to return the minimum key from the tree
int minimum(Proto_Van_Emde_Boas* helper)
{
// Base case choses the least key
// present in the cluster
if (helper->universe_size == 2) {
if (helper->clusters[0]) {
return 0;
}
else if (helper->clusters[1]) {
return 1;
}
// No keys present then return -1
return -1;
}
else {
// Recursively find in summary for
// first 1 present in Proto-VEB
int minimum_cluster = minimum(helper->summary);
int offset;
// If no key is present in
// the cluster then return -1
if (minimum_cluster == -1) {
return -1;
}
else {
// Recursively find the position of the key
// in the minimum_cluster
offset = minimum(helper->clusters[minimum_cluster]);
// Returns overall index of minimum key
return helper->generate_index(minimum_cluster, offset);
}
}
}
// Function to return the maximum key from the tree
int maximum(Proto_Van_Emde_Boas* helper)
{
// Return the maximum key present in
// the cluster
if (helper->universe_size == 2) {
if (helper->clusters[1]) {
return 1;
}
else if (helper->clusters[0]) {
return 0;
}
// Return -1 if no keys present in the
// cluster
return -1;
}
else {
// Recursively find the last 1 present
// in the summary
int maximum_cluster = maximum(helper->summary);
int offset;
// If no key is present in
// the cluster then return -1
if (maximum_cluster == -1) {
return -1;
}
else {
// Recursively find the position of the key
// in the maximum_cluster
offset = maximum(helper->clusters[maximum_cluster]);
return helper->generate_index(maximum_cluster, offset);
}
}
}
// Function to delete a key from the tree
void pveb_delete(Proto_Van_Emde_Boas*& helper, int key)
{
// Base case: If the key is present
// then make it nullptr
if (helper->universe_size == 2) {
if (helper->clusters[key]) {
delete helper->clusters[key];
helper->clusters[key] = nullptr;
}
}
else {
// Recursive delete to reach at the base case
pveb_delete(helper->clusters[helper->high(key)], helper->low(key));
bool isanyinCluster = false;
// Iterate over the cluster of keys to check whether
// any other key is present within that cluster
// If yes then we should not update summary to 0
// else update summary to 0
for (int i = helper->high(key) * helper->root(helper->universe_size);
i < (helper->high(key) + 1) * helper->root(helper->universe_size);
i++) {
// If member is present then break the loop
if (isMember(helper->clusters[helper->high(key)], i)) {
isanyinCluster = true;
break;
}
}
// If no member is present then
// update summary to zero
if (isanyinCluster == false) {
pveb_delete(helper->summary, helper->high(key));
}
}
}
// Driver code
int main()
{
Proto_Van_Emde_Boas* hello = new Proto_Van_Emde_Boas(4);
cout << boolalpha;
insert(hello, 2);
insert(hello, 3);
cout << minimum(hello) << endl;
cout << maximum(hello) << endl;
}
Tanto la consulta mínima como la máxima se ejecutan en una complejidad de tiempo O(log2(u)).
Relación de recurrencia:
T(u) = 2T() + O(1)
Publicación traducida automáticamente
Artículo escrito por Aakash_Panchal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA