Dados dos enteros X y K , la tarea es determinar si existe un número que tenga exactamente X factores de los cuales K es primo.
Ejemplos:
Entrada: X = 8, K = 1
Salida: Sí
Explicación:
El número es 128
Factores de 128 = {1, 2, 4, 8, 16, 32, 64, 128} que son 8 en cuenta = X
Entre estos, solo 2 es primo. Por lo tanto cuenta de factor primo = 1 = K
Entrada: X = 4, K = 2
Salida: Sí
Explicación:
El número es 6
Factores de 6 = {1, 2, 3, 6} que son 4 en cuenta = X
Entre estos, solo 2 y 3 son primos. Por lo tanto cuenta de factor primo = 2 = K
Acercarse:
- Supongamos que un número N tiene X factores de los cuales K son primos, digamos

- Por lo tanto, el número se puede escribir como
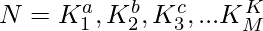 donde, el número total de factores se calcula mediante
donde, el número total de factores se calcula mediante 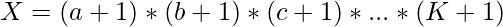
- Se observa que X es un producto de “ potencia+1 ” de los factores primos del número. Por lo tanto, si podemos dividir X en un producto de K números, entonces podemos formar un número con exactamente X factores de los cuales K es primo.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to check if there exists
// a number with X factors
// out of which exactly K are prime
#include <bits/stdc++.h>
using namespace std;
// Function to check if such number exists
bool check(int X, int K)
{
int prime, temp, sqr, i;
// To store the sum of powers
// of prime factors of X which
// determines the maximum count
// of numbers whose product can form X
prime = 0;
temp = X;
sqr = sqrt(X);
// Determining the prime factors of X
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
// To check if the number is prime
if (temp > 2)
prime++;
// If X is 1, then we cannot form
// a number with 1 factor and K
// prime factor (as K is atleast 1)
if (X == 1)
return false;
// If X itself is prime then it
// can be represented as a power
// of only 1 prime factor which
// is X itself so we return true
if (prime == 1 && K == 1)
return true;
// If sum of the powers of prime factors
// of X is greater than or equal to K,
// which means X can be represented as a
// product of K numbers, we return true
else if (prime >= K)
return true;
// In any other case, we return false
// as we cannot form a number with X
// factors and K prime factors
else
return false;
}
// Driver code
int main()
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
cout << "Yes";
else
cout << "No";
}
Java
// Java program to check if there exists
// a number with X factors
// out of which exactly K are prime
import java.util.*;
class GFG{
// Function to check if such number exists
static boolean check(int X, int K)
{
int prime, temp, sqr, i;
// To store the sum of powers
// of prime factors of X which
// determines the maximum count
// of numbers whose product can form X
prime = 0;
temp = X;
sqr = (int) Math.sqrt(X);
// Determining the prime factors of X
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
// To check if the number is prime
if (temp > 2)
prime++;
// If X is 1, then we cannot form
// a number with 1 factor and K
// prime factor (as K is atleast 1)
if (X == 1)
return false;
// If X itself is prime then it
// can be represented as a power
// of only 1 prime factor which
// is X itself so we return true
if (prime == 1 && K == 1)
return true;
// If sum of the powers of prime factors
// of X is greater than or equal to K,
// which means X can be represented as a
// product of K numbers, we return true
else if (prime >= K)
return true;
// In any other case, we return false
// as we cannot form a number with X
// factors and K prime factors
else
return false;
}
// Driver code
public static void main(String[] args)
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
System.out.print("Yes");
else
System.out.print("No");
}
}
// This code contributed by Rajput-Ji
Python3
# Python3 program to check if there exists
# a number with X factors
# out of which exactly K are prime
from math import sqrt
# Function to check if such number exists
def check(X,K):
# To store the sum of powers
# of prime factors of X which
# determines the maximum count
# of numbers whose product can form X
prime = 0
temp = X
sqr = int(sqrt(X))
# Determining the prime factors of X
for i in range(2,sqr+1,1):
while (temp % i == 0):
temp = temp // i
prime += 1
# To check if the number is prime
if (temp > 2):
prime += 1
# If X is 1, then we cannot form
# a number with 1 factor and K
# prime factor (as K is atleast 1)
if (X == 1):
return False
# If X itself is prime then it
# can be represented as a power
# of only 1 prime factor w0hich
# is X itself so we return true
if (prime == 1 and K == 1):
return True
# If sum of the powers of prime factors
# of X is greater than or equal to K,
# which means X can be represented as a
# product of K numbers, we return true
elif(prime >= K):
return True
# In any other case, we return false
# as we cannot form a number with X
# factors and K prime factors
else:
return False
# Driver code
if __name__ == '__main__':
X = 4
K = 2
if (check(X, K)):
print("Yes")
else:
print("No")
# This code is contributed by Surendra_Gangwar
C#
// C# program to check if there exists
// a number with X factors
// out of which exactly K are prime
using System;
class GFG{
// Function to check if such number exists
static bool check(int X, int K)
{
int prime, temp, sqr, i;
// To store the sum of powers
// of prime factors of X which
// determines the maximum count
// of numbers whose product can form X
prime = 0;
temp = X;
sqr = Convert.ToInt32(Math.Sqrt(X));
// Determining the prime factors of X
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
// To check if the number is prime
if (temp > 2)
prime++;
// If X is 1, then we cannot form
// a number with 1 factor and K
// prime factor (as K is atleast 1)
if (X == 1)
return false;
// If X itself is prime then it
// can be represented as a power
// of only 1 prime factor which
// is X itself so we return true
if (prime == 1 && K == 1)
return true;
// If sum of the powers of prime factors
// of X is greater than or equal to K,
// which means X can be represented as a
// product of K numbers, we return true
else if (prime >= K)
return true;
// In any other case, we return false
// as we cannot form a number with X
// factors and K prime factors
else
return false;
}
// Driver code
static public void Main ()
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
// This code is contributed by shubhamsingh10
Javascript
<script>
// javascript program to check if there exists
// a number with X factors
// out of which exactly K are prime
// Function to check if such number exists
function check(X , K) {
var prime, temp, sqr, i;
// To store the sum of powers
// of prime factors of X which
// determines the maximum count
// of numbers whose product can form X
prime = 0;
temp = X;
sqr = parseInt( Math.sqrt(X));
// Determining the prime factors of X
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = parseInt(temp / i);
prime++;
}
}
// To check if the number is prime
if (temp > 2)
prime++;
// If X is 1, then we cannot form
// a number with 1 factor and K
// prime factor (as K is atleast 1)
if (X == 1)
return false;
// If X itself is prime then it
// can be represented as a power
// of only 1 prime factor which
// is X itself so we return true
if (prime == 1 && K == 1)
return true;
// If sum of the powers of prime factors
// of X is greater than or equal to K,
// which means X can be represented as a
// product of K numbers, we return true
else if (prime >= K)
return true;
// In any other case, we return false
// as we cannot form a number with X
// factors and K prime factors
else
return false;
}
// Driver code
var X, K;
X = 4;
K = 2;
if (check(X, K))
document.write("Yes");
else
document.write("No");
// This code contributed by gauravrajput1
</script>
Yes
Complejidad de tiempo: O(sqrt(n) * log n)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por shreysingh3105 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA